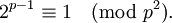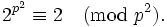- 3511
-
Eine Wieferich-Primzahl ist eine Primzahl p mit der Eigenschaft, dass 2p−1 − 1 durch p2 teilbar ist.
Alternativ kann man dies auch als Kongruenz schreiben:
Solche Primzahlen wurden 1909 von dem deutschen Mathematiker Arthur Wieferich erstmals beschrieben.
Inhaltsverzeichnis
Bekannte Wieferich-Primzahlen
Man kennt bisher nur zwei Wieferich-Primzahlen, nämlich 1093 (gefunden im Jahr 1913 von Waldemar Meissner) und 3511 (gefunden im Jahr 1922 von N. G. W. H. Beeger). Mit Computerhilfe hat man bis Juni 2003 alle Zahlen bis 1,25 · 1015 untersucht, weitere Wieferich-Primzahlen fand man dabei nicht.
Verwandtschaft mit dem großen fermatschen Satz
Wieferich beschäftigte sich mit dem großen Fermatschen Satz. 1909 veröffentlichte er als Ergebnis den folgenden Satz:
Voraussetzung: Sei xp + yp + zp = 0 wobei x,y,z ganze Zahlen und p > 2 eine Primzahl ist. Weiterhin sei das Produkt
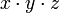 nicht teilbar durch p.
nicht teilbar durch p.Behauptung: p ist eine Wieferich-Primzahl, d.h. ap − 1 − 1 ist teilbar durch p2 mit a = 2.
1910 zeigte der Mathematiker Mirimanoff, dass dieser Satz auch für a = 3 gilt. Inzwischen weiß man, dass es keine Primzahlen gibt, die die Voraussetzungen des Satzes erfüllen.
Eigenschaften von Wieferich-Primzahlen
- Es ist nicht bekannt, ob es unendlich viele Wieferich-Primzahlen gibt. Man vermutet, dass dies nicht der Fall ist.
- Aus der Wieferich-Primzahl w kann die Mersenne-Zahl Mn = Mw-1 = 2w-1 -1 als Produkt Mw-1 = k*w2 konstruiert werden.
- n = w-1 ist somit (trivialer Weise, da n geradzahlig) nicht prim, und Mn keine Mersenne-Primzahl (s. dort).
- Offen ist die Frage, ob es Mersenne-Zahlen Mp < Mw-1 (mit primen Exponenten p) gibt, die durch w2 teilbar sind. Dabei muss p ein Teiler von w-1 sein, wenn Mp durch w teilbar sein soll.
- Dieser Sachverhalt kann mit gruppentheoretischen Begriffen ausgedrückt werden:
- Da w-1 nicht prim ist, handelt es sich bei 2w-1-1 nicht um eine mersennesche Zahl. Es müsste also eine mersennesche Zahl 2p-1 mit p=(w-1)/x geben, die durch w2 teilbar ist; d.h. dass die Länge g(w) der multiplikativen zyklischen Subgruppe von w zur Basis 2 prim sein müsste.
- Es sind aber empirisch die Gruppenordnungen der einzigen bekannten Wieferichprimzahlen g(1093) = 364 = 4*7*13 und g(3511)=1755 = 33*5*13 nicht prim.
- Dass Mersenne-Zahlen quadratfrei sind, scheint bisher nur ein empirisches Resultat zu sein. Mathworld formuliert bspw. "Alle bekannten Mersenne Zahlen 2p - 1 sind quadratfrei. Allerdings vermutet GUY (1994), dass es Mersenne-Zahlen gibt, die nicht quadratfrei sind".[1]
- Unterschied zu anderen Basen als 2: für andere Basen als 2 und die entsprechenden Äquivalente zu Mersenne- und Wieferichzahlen trifft dies nicht zu.
- Bspw. ist zur Basis 3 mit (35 - 1)/(3-1) = 112 die Bedingung w2 teilt 3p-1 (w,p prim) erfüllt.
- Zur Basis 2819 tritt w=19 bei 28193 - 1 = x*194 das Wieferich-analog w=19 sogar zur Potenz 4 auf. Die Quadratfreiheit von Mersenne-Zahlen (zur Basis 2) muss demnach eine besondere Eigenschaft der Basis 2 (und möglicherweise weiterer Basen) sein, falls sie generell zutreffen sollte.
- Für eine Wieferich-Primzahl p gilt:
- Mit 2n = 1 (mod p) tritt stets gleichzeitig 2n = 1 (mod p2) auf.
Siehe auch
Einzelnachweis
Literatur
- A. Wieferich: Zum letzten Fermat'schen Theorem. In: Journal für Reine Angewandte Math. 136. 1909, 293-302.
- J. H. Silverman: Wieferich's criterion and the abc-conjecture. In: Journal Number Theory. 30 (2). 1988, 226-237.
Weblinks
Wikimedia Foundation.