- Artinscher Ring
-
Der Begriff artinscher Ring oder artinscher Modul (nach Emil Artin) beschreibt im mathematischen Teilgebiet der Algebra eine gewisse Endlichkeitsbedingung.
Inhaltsverzeichnis
Definition
Ein Modul M über einem Ring mit 1 heißt artinsch, wenn er eine der folgenden äquivalenten Bedingungen erfüllt:
- (absteigende Kettenbedingung) Jede absteigende Folge von Untermoduln wird stationär, d.h. in einer Kette
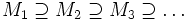 gibt es einen Index N, so dass
gibt es einen Index N, so dass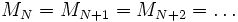 gilt.
gilt.
- (Minimalbedingung für Untermoduln) Jede nichtleere Menge von R-Untermoduln von M hat ein minimales Element bezüglich Inklusion.
Ein Ring R heißt linksartinsch, wenn R artinsch als R-Linksmodul ist.Ein Ring R heißt rechtsartinsch, wenn R artinsch als R-Rechtsmodul ist.
Ein Ring R heißt artinsch, wenn R links- und rechtsartinsch ist.
Die Untermoduln sind dann gerade die Ideale.
Eigenschaften
- Ist R eine (assoziative) Algebra über einem Körper K, und hat ein R-Modul M endliche K-Dimension, so ist M artinsch.
- Ein kommutativer Ring mit Einselement ist genau dann artinsch, wenn er noethersch und nulldimensional ist. (Ein Ring ist nulldimensional, wenn jedes Primideal maximal ist.) Insbesondere ist jeder Körper artinsch.
- Endlich erzeugte Moduln über einem artinschen Ring sind artinsch.
- Ein artinscher Integritätsring ist bereits ein Körper, es gilt sogar folgende stärkere Aussage: Ein Integritätsring, der die absteigende Kettenbedingung für Hauptideale erfüllt, ist ein Körper.
- Ein linksartinscher Ring ist auch linksnoethersch. (die Umkehrung gilt i.A. nicht, auch gilt dies nicht für R-Moduln)
Beispiele
- Ist K ein Körper, so sind die Ringe
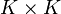 und K[T] / (Tn) artinsch.
und K[T] / (Tn) artinsch. - Die
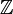 -Moduln
-Moduln 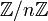 sind artinsch,
sind artinsch, 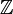 selbst jedoch nicht.
selbst jedoch nicht. 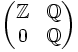 ist rechtsnoethersch, aber weder linksartinsch noch linksnoethersch.
ist rechtsnoethersch, aber weder linksartinsch noch linksnoethersch.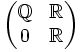 ist rechtsartinsch, aber nicht linksartinsch.
ist rechtsartinsch, aber nicht linksartinsch.
Siehe auch
Wikimedia Foundation.
