- Arzela-Ascoli
-
Der Satz von Arzelà-Ascoli, benannt nach Cesare Arzelà (1847-1912) in Erweiterung eines Satzes von Giulio Ascoli (1843-1896), ist ein wichtiger Satz in der Funktionalanalysis. Er lautet:
Sei X ein kompakter metrischer Raum, Y ein Banachraum und
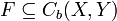 eine Familie (Teilmenge) stetiger und beschränkter Funktionen
eine Familie (Teilmenge) stetiger und beschränkter Funktionen 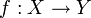 . Dann gilt: Die Funktionenfamilie F ist genau dann relativ kompakt in Cb(X,Y), wenn F gleichgradig stetig ist und für jedes
. Dann gilt: Die Funktionenfamilie F ist genau dann relativ kompakt in Cb(X,Y), wenn F gleichgradig stetig ist und für jedes 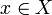 die Menge
die Menge 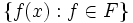 der Funktionswerte in x relativ kompakt in Y ist.
der Funktionswerte in x relativ kompakt in Y ist.Beweisskizze
Der Beweis benutzt das cantorsche Diagonalverfahren, in welchem auf rekursive Art partiell konvergente Teilfolgen konstruiert werden, um dann quer durch alle Teilfolgen eine überall konvergente Teilfolge zu erhalten.
Sei
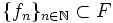 eine beliebige Funktionenfolge in der Funktionenfamilie F. Zu zeigen ist, dass diese eine in Cb(X,Y) konvergente Teilfolge enthält.
eine beliebige Funktionenfolge in der Funktionenfamilie F. Zu zeigen ist, dass diese eine in Cb(X,Y) konvergente Teilfolge enthält.Dazu wählt man sich eine aufsteigende Folge von endlichen Teilmengen
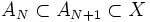 , welche gegen eine in der kompakten Punktmenge X dichte Teilmenge
, welche gegen eine in der kompakten Punktmenge X dichte Teilmenge 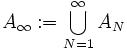 „konvergiert“.
„konvergiert“.Die Funktionenfolge, eingeschränkt auf eine solche Punktmenge,
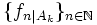 , enthält nach Voraussetzung eine auf Ak konvergente Teilfolge, denn ein endliches kartesisches Produkt relativ kompakter Mengen ist wieder relativ kompakt.
, enthält nach Voraussetzung eine auf Ak konvergente Teilfolge, denn ein endliches kartesisches Produkt relativ kompakter Mengen ist wieder relativ kompakt.Sei
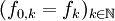 die nullte, triviale Teilfolge. Dann kann rekursiv, beginnend mit
die nullte, triviale Teilfolge. Dann kann rekursiv, beginnend mit 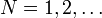 , in der Funktionenfolge
, in der Funktionenfolge 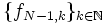 eine Teilfolge
eine Teilfolge 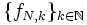 ausgewählt werden, die auf der vergrößerten Punktmenge AN konvergiert. Schlussendlich konvergiert nach dem Cantorschen Diagonal„trick“, die Diagonalfolge
ausgewählt werden, die auf der vergrößerten Punktmenge AN konvergiert. Schlussendlich konvergiert nach dem Cantorschen Diagonal„trick“, die Diagonalfolge 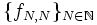 auf der dichten Teilmenge
auf der dichten Teilmenge 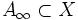 gegen eine Funktion
gegen eine Funktion 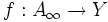 .
.Aus der gleichgradigen Stetigkeit folgt, dass die so erhaltene Grenzfunktion auf ganz X stetig und beschränkt fortgesetzt werden kann zu
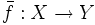 und es folgt ebenfalls, dass die Diagonalfolge auch in der Supremumsnorm gegen die so konstruierte Funktion konvergiert:
und es folgt ebenfalls, dass die Diagonalfolge auch in der Supremumsnorm gegen die so konstruierte Funktion konvergiert: 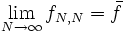 in Cb(X,Y), das heißt
in Cb(X,Y), das heißt-
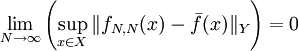 .
.
Literatur
- Cesare Arzelà: Un' osservazione intorno alle serie di funzioni. Rend. dell' Accad. R. delle Sci. dell'Istituto di Bologna, S. 142–159 (1882–1883).
- Cesare Arzelà: Sulle funzioni di linee. Mem. Accad. Sci. Ist. Bologna Cl. Sci. Fis. Mat. Vol. 5 No 5, S. 55–74 (1895).
- Giulio Ascoli: Le curve limiti di una varietà data di curve. Atti della R. Accad. dei Lincei Memorie della Cl. Sci. Fis. Mat. Nat.Vol 18 No 3, S. 521–586 (1883–1884).
- Walter Rudin: Principles of mathematical analysis. McGraw-Hill 1976, ISBN 978-0070542358, S. 154ff.
- Johann Cigler, Hans-Christian Reichel: Topologie. Eine Grundvorlesung, ISBN 3411051213.
- Harry Poppe: Compactness in General Function Spaces. Berlin 1974.
-
Wikimedia Foundation.
