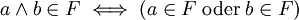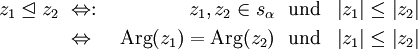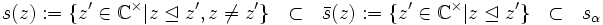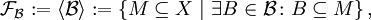- Ordnungsideal
-
In der Mathematik ist ein Filter eine nichtleere, nach unten gerichtete Oberhalb-Menge.
Ein Filter ist eine Teilmenge einer halbgeordneten Menge mit bestimmten Eigenschaften. Anschaulich betrachtet enthält ein Filter Elemente, die „zu groß“ sind als dass sie den Filter passieren könnten. Ist x ein Filterelement so auch jedes größere Element, und je zwei Filterelemente x und y enthalten einen gemeinsamen Kern z, der selbst schon zu groß ist, als dass er den Filter passieren könnte.
Filter in der umgekehrten Halbordnung heißen Ideale der Ordnung oder Ordnungsideale.
Inhaltsverzeichnis
Anwendungen
Filter treten in der Theorie der Ordnungen und Verbände auf. Ein wichtiger Spezialfall sind Mengenfilter, d. h. Filter in der durch Mengeninklusion geordneten Potenzmenge einer Menge. Mengenfilter werden besonders in der Topologie verwendet und erlauben dort die Verallgemeinerung des Begriffs der Folge für topologische Räume ohne abzählbare Umgebungsbasis. So bildet das System der Umgebungen
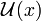 eines Punktes x in einem topologischen Raum einen speziellen Filter, den Umgebungsfilter. Umgebungsfilter können in Räumen, die kein Abzählbarkeitsaxiom erfüllen, zur Definition von Netzen verwendet werden, die die Rolle der Folgen aus der elementaren Analysis teilweise übernehmen. Man fasst dazu einen Filter als gerichtete Menge auf und betrachtet Netze auf dieser gerichteten Menge.
eines Punktes x in einem topologischen Raum einen speziellen Filter, den Umgebungsfilter. Umgebungsfilter können in Räumen, die kein Abzählbarkeitsaxiom erfüllen, zur Definition von Netzen verwendet werden, die die Rolle der Folgen aus der elementaren Analysis teilweise übernehmen. Man fasst dazu einen Filter als gerichtete Menge auf und betrachtet Netze auf dieser gerichteten Menge.Mit einem Ultrafilter (der kein Hauptfilter ist) auf den natürlichen Zahlen lassen sich die hyperreellen Zahlen der Nichtstandardanalysis „konstruieren“. Allerdings wird die Existenz solcher Filter selbst nur durch das Auswahlaxiom – also nicht konstruktiv – gesichert.
Allgemeine Definitionen
Eine nichtleere Teilmenge F einer halbgeordneten Menge
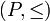 heißt Filter, wenn folgende Bedingungen erfüllt sind:
heißt Filter, wenn folgende Bedingungen erfüllt sind:- F ist eine Oberhalb-Menge:
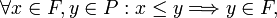
(D.h. alle (mit x in Relation stehenden) Elemente, die größer als x sind, sind Teil des Filters.) - F ist nach unten gerichtet:
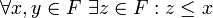 und
und 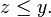
(D.h. F ist bzgl. der Umkehrrelation der betrachteten Halbordnung gerichtet.)
Ein Filter heißt echter Filter, wenn er nicht ganz (also ungleich) P ist.
Jeder Filter auf einer halbgeordneten Menge P ist Element der Potenzmenge von P. Die Menge der auf derselben halbgeordneten Menge definierten Filter wird durch die Inklusionsrelation ihrerseits halbgeordnet. Sind F1 und F2 Filter auf derselben halbgeordneten Menge P, so heißt F2 feiner als F1 (F1 gröber als F2), wenn
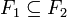 . Ein maximal feiner echter Filter heißt Ultrafilter.
. Ein maximal feiner echter Filter heißt Ultrafilter.Filter in Verbänden
Während diese Definition von "Filter" die allgemeinste für beliebige halbgeordnete Mengen ist, wurden Filter ursprünglich für Verbände definiert. In diesem Spezialfall ist ein Filter eine nichtleere Teilmenge F des Verbandes
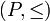 , die eine Oberhalb-Menge ist und abgeschlossen unter endlichen Infima, d.h. für alle
, die eine Oberhalb-Menge ist und abgeschlossen unter endlichen Infima, d.h. für alle 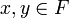 ist auch
ist auch 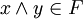 .
.Hauptfilter
Der kleinste Filter, der ein vorgegebenes Element p enthält, ist
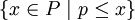 . Filter dieser Form heißen Hauptfilter, und p ein Hauptelement des Filters. Der zu p gehörende Hauptfilter wird als
. Filter dieser Form heißen Hauptfilter, und p ein Hauptelement des Filters. Der zu p gehörende Hauptfilter wird als 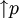 geschrieben.
geschrieben.Primfilter
Ein echter Filter F in einem Verband P mit der Zusatzeigenschaft
heißt Primfilter.
Ideal
Betrachtet man in einer halbgeordneten Menge
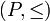 die Umkehrrelation
die Umkehrrelation 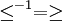 , so ist auch
, so ist auch 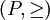 wieder eine halbgeordnete Menge, ebenso erhält man aus einem (distributiven) Verband
wieder eine halbgeordnete Menge, ebenso erhält man aus einem (distributiven) Verband 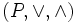 durch Vertauschen der beiden Verbandsverküpfungen Supremum
durch Vertauschen der beiden Verbandsverküpfungen Supremum 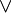 und Infimum
und Infimum 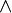 wieder einen (distributiven) Verband. Sind in P ein kleinstes Element 0 und ein größtes Element 1 vorhanden, so werden sie ebenfalls vertauscht. In allen genannten Fällen wird die so durch Dualisierung entstehende Struktur als
wieder einen (distributiven) Verband. Sind in P ein kleinstes Element 0 und ein größtes Element 1 vorhanden, so werden sie ebenfalls vertauscht. In allen genannten Fällen wird die so durch Dualisierung entstehende Struktur als 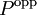 notiert.
notiert.Ein Filter in
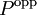 heißt ein Ordnungsideal oder auch kurz Ideal in P.
heißt ein Ordnungsideal oder auch kurz Ideal in P.Beispiel
Wir betrachten in der sog. punktierten komplexen Ebene
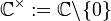 die Teilmengen
die Teilmengen 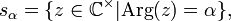 für
für 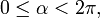 der (offenen) Strahlen aus der Null (kurz: Nullstrahlen). Auf
der (offenen) Strahlen aus der Null (kurz: Nullstrahlen). Auf 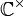 definieren wir nun eine Halbordnung
definieren wir nun eine Halbordnung 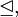 indem wir
indem wir 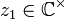 als kleiner-gleich
als kleiner-gleich 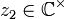 betrachten, falls z1 und z2 auf demselben Strahl liegen und z1 betraglich kleiner-gleich z2 ist. D.h.
betrachten, falls z1 und z2 auf demselben Strahl liegen und z1 betraglich kleiner-gleich z2 ist. D.h.für alle
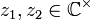 und
und 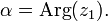
In der halbgeordneten Menge
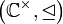 sind nun alle Filter gegeben durch die Nullstrahlen und deren offenen und abgeschlossenen Teilstrahlen
sind nun alle Filter gegeben durch die Nullstrahlen und deren offenen und abgeschlossenen Teilstrahlenfür alle
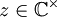 und
und 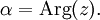 Jeder dieser Filter ist echt. Außerdem folgt aus
Jeder dieser Filter ist echt. Außerdem folgt aus 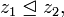 dass
dass 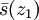 feiner
feiner 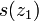 feiner
feiner 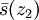 feiner
feiner 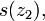 insbesondere ist
insbesondere ist 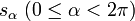 ein maximal-feiner echter Filter und damit ein Ultrafilter. Für jede komplexe Zahl
ein maximal-feiner echter Filter und damit ein Ultrafilter. Für jede komplexe Zahl 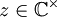 ist der abgeschlossene Strahl
ist der abgeschlossene Strahl 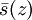 ihr Hauptfilter
ihr Hauptfilter 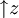 mit z als (einzigem) Hauptelement.
mit z als (einzigem) Hauptelement.Die Ordnungsideale in
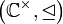 entsprechen den fehlenden Strahlenabschnitten zwischen der Null und dem Beginn jedes Teilstrahls. Ist der Teilstrahl offen, enthält also nicht seinen Aufpunkt, so fehlt auch im entsprechenden Ordnungsideal der Aufpunkt – analog ist er im abgeschlossenen Fall in Teilstrahl und Ideal jeweils enthalten. (Filter und Ordnungsideal sind also nicht disjunkt!) Aus dem Nullstrahl ergibt sich kein entsprechendes Ordnungsideal, da der „fehlende“ Strahlenabschnitt durch die leere Menge gegeben wäre (die kein Filter sein kann). Die Ideale haben also die Form:
entsprechen den fehlenden Strahlenabschnitten zwischen der Null und dem Beginn jedes Teilstrahls. Ist der Teilstrahl offen, enthält also nicht seinen Aufpunkt, so fehlt auch im entsprechenden Ordnungsideal der Aufpunkt – analog ist er im abgeschlossenen Fall in Teilstrahl und Ideal jeweils enthalten. (Filter und Ordnungsideal sind also nicht disjunkt!) Aus dem Nullstrahl ergibt sich kein entsprechendes Ordnungsideal, da der „fehlende“ Strahlenabschnitt durch die leere Menge gegeben wäre (die kein Filter sein kann). Die Ideale haben also die Form: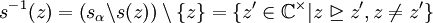 und
und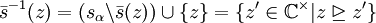
für alle
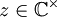 und
und 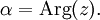
Mengenfilter
Ein wichtiger Spezialfall eines Filters – vor allem in der Topologie – sind Mengenfilter. Man geht in diesem Fall von der durch die Mengeninklusion halbgeordnete Potenzmenge
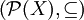 einer beliebigen nichtleeren Mengen X aus. Eine echte Teilmenge
einer beliebigen nichtleeren Mengen X aus. Eine echte Teilmenge 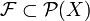 ist genau dann ein Mengenfilter oder Filter, wenn folgende Eigenschaften erfüllt sind
ist genau dann ein Mengenfilter oder Filter, wenn folgende Eigenschaften erfüllt sind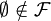 und
und 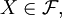
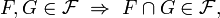
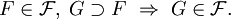
Diese Definition stimmt mit der oben gegebenen für echte Filter in Verbänden überein, da die Potenzmenge von X einen Verband bildet.
- Beispiele für Mengenfilter
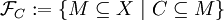 heißt der von
heißt der von 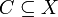 erzeugte Hauptfilter.
erzeugte Hauptfilter.- Ist
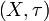 ein topologischer Raum mit Topologie τ, dann heißt
ein topologischer Raum mit Topologie τ, dann heißt 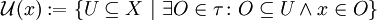 Umgebungsfilter von x.
Umgebungsfilter von x. - Ist S eine unendliche Menge, dann heißt
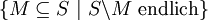 Fréchet-Filter der Menge S.
Fréchet-Filter der Menge S. - Ist
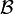 ein nichtleeres Mengensystem von
ein nichtleeres Mengensystem von 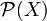 mit folgenden Eigenschaften
mit folgenden Eigenschaften
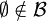 und
und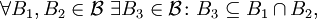
- so heißt
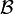 Filterbasis in X. Ein solches Mengensystem erzeugt auf natürliche Weise einen Filter
Filterbasis in X. Ein solches Mengensystem erzeugt auf natürliche Weise einen Filter
- Dieser heißt der von
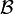 erzeugte Filter.
erzeugte Filter.
- Ist
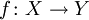 eine Abbildung zwischen zwei nichtleeren Mengen und
eine Abbildung zwischen zwei nichtleeren Mengen und 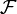 ein Filter auf X, so bezeichnet
ein Filter auf X, so bezeichnet 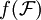 den von der Filterbasis
den von der Filterbasis 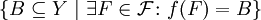 erzeugten Filter. Dieser heißt Bildfilter von f.
erzeugten Filter. Dieser heißt Bildfilter von f.
Anwendungen in der Topologie
In der Topologie ersetzen Filter und Netze die dort i. Allg. unzureichenden Folgen. Man erhält dadurch oft analoge Sätze zu denen in metrischen Räumen.
Ist (X,τ) ein topologischer Raum, dann sagt man, ein Filter
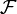 konvergiert gegen ein
konvergiert gegen ein 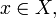 wenn
wenn 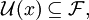 d. h., wenn
d. h., wenn 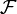 feiner ist als der Umgebungsfilter
feiner ist als der Umgebungsfilter 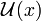 von x. Schreibweise:
von x. Schreibweise: 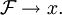
So ist zum Beispiel eine Abbildung
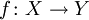 zwischen zwei topologischen Räumen genau dann stetig, wenn für jeden Filter
zwischen zwei topologischen Räumen genau dann stetig, wenn für jeden Filter 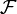 mit
mit 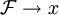 gilt, dass
gilt, dass 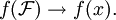 Hier zeigt sich, dass Filter ein durchaus brauchbares Hilfsmittel sind, topologische Eigenschaften zu charakterisieren.
Hier zeigt sich, dass Filter ein durchaus brauchbares Hilfsmittel sind, topologische Eigenschaften zu charakterisieren.Beachte, dass in einem nicht-hausdorffschen Raum ein Filter nicht gegen einen einzelnen Punkt konvergieren muss.
Siehe auch
Literatur
Zu den allgemeinen, ordnungs- und verbandstheoretischen Begriffsbildungen und ihren Anwendungen:
- Niels Schwartz: Spektrale Räume und Spektren in der Algebra. (Skript) PDF-Version, HTML-Version.
Zu den Anwendungen in der mengentheoretischen Topologie:
- Boto v. Querenburg: Mengentheoretische Topologie. 3. Auflage. Springer, Berlin 2001, ISBN 3540677909.
- Thorsten Camps, Stefan Kühling und Gerhard Rosenberger: Einführung in die mengentheoretische und die algebraische Topologie. Heldermann, 2006, ISBN 3-88538-115-X.
- F ist eine Oberhalb-Menge:
Wikimedia Foundation.