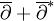- Atiyah-Singer-Indextheorem
-
Der Atiyah-Singer-Indexsatz (Atiyah–Singer index theorem) besagt, dass für einen elliptischen Differentialoperator auf einer kompakten Mannigfaltigkeit der analytische Index (eng verbunden mit der Dimension des Lösungsraums) gleich dem topologischen Index (über topologische Invariante definiert) ist. Viele andere wichtige Sätze wie der Satz von Riemann-Roch sind Spezialfälle. Der Satz hat auch Anwendungen in der theoretischen Physik. Er wurde 1963 von Michael Atiyah und Isadore M. Singer bewiesen. Sie erhielten dafür den Abelpreis 2004.
Inhaltsverzeichnis
Notation
- X ist eine glatte kompakte Mannigfaltigkeit M (ohne Rand).
- E und F sind glatte Vektorbündel über X.
- D ist ein elliptischer Differentialoperator von E auf F. Das heißt in lokalen Koordinaten wirkt er als Differentialoperator, der glatte Schnitte des Vektorbündels E auf solche von F abbildet.
Das Symbol eines Differentialoperators
Falls D ein Differentialoperator der Ordnung n in k Variablen
- x1,...,xk,
ist, ist sein „Symbol“[1] eine Funktion der 2k Variablen
- x1,...,xk,y1,...,yk,
die dadurch gegeben ist, dass man alle Terme von geringerer Ordnung als n weglässt und ∂/∂xi durch yi ersetzt. Das Symbol ist also homogen in den Variablen y vom Grad n. Es ist wohldefiniert, obwohl ∂/∂xi nicht mit xi kommutiert, da nur der höchste Term behalten wurde und Differentialoperatoren nur bis auf niedrigere Terme kommutieren. Der Operator wird elliptisch genannt, falls das Symbol ungleich 0 ist, wenn mindestens ein y ungleich 0 ist.
Beispiel für n=2: Der Laplaceoperator in k Variablen hat das Symbol y12 + ... + yk2, und ist somit elliptisch, da es ungleich 0 ist, wenn einer der y ungleich 0 ist. Die Wellengleichung hat dagegen das Symbol −y12 + ... + yk2, das für k ≥ 2 nicht elliptisch ist. Das Symbol verschwindet hier für einige y ungleich 0.
Das Symbol eines Differentialoperators der Ordnung n auf einer glatten Mannigfaltigkeit X ist ganz ähnlich definiert unter Benutzung lokaler Koordinatenkarten. Es ist eine Funktion des Ko-Tangenten-Bündels von X und ist homogen vom Grad n auf jedem Ko-Tangential-Raum[2]. Allgemeiner ist das Symbol eines Differentialoperators zwischen zwei Vektorbündeln E und F ein Schnitt des pullback des Bündels
- Hom(E, F)
zum Kotangentialraum von X. Der Differentialoperator heißt elliptisch wenn das Element von Hom(Ex, Fx) für alle Kotangential-Vektoren ungleich 0 bei jedem Punkt x von X invertierbar ist.
Eine wichtige Eigenschaft elliptischer Operatoren ist, dass sie fast invertierbar sind, was eng damit verbunden ist dass ihre Symbole fast invertierbar sind. Genauer: ein elliptischer Operator D auf einer kompakten Mannigfaltigkeit hat eine (nicht eindeutige) Pseudoinverse D′ so dass DD′ − 1 und D′D − 1 beide kompakte Operatoren sind. Eine wichtige Folge ist, dass der Kern von D endlichdimensional ist, da alle Eigenräume kompakter Operatoren endlichdimensional sind. [3]
Der analytische Index
Da der elliptische Differentialoperator D ein Pseudoinverses hat, ist er ein Fredholmoperator. Jeder Fredholmoperator hat einen Index, definiert als Differenz der (endlichen) Dimensionen der Kerne von D (also der Lösungen von Df = 0) und der Ko-Kerne von D (die Einschränkungen der rechten Seite von inhomogenen Gleichungen wie Df = g, oder äquivalent: der Kern des adjungierten Operators D*), also
- Index(D) = Dim Ker(D) − Dim Coker(D) = Dim Ker(D) − Dim Ker(D*).
Dies wird der analytische Index von D genannt.
Beispiel für n=1: Angenommen die Mannigfaltigkeit sei ein Kreis (als
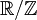 gedacht), und D ist der Operator d/dx − λ für eine komplexe Konstante λ (das einfachste Beispiel eines elliptischen Operators). Dann ist der Kern der von den Termen der Form
gedacht), und D ist der Operator d/dx − λ für eine komplexe Konstante λ (das einfachste Beispiel eines elliptischen Operators). Dann ist der Kern der von den Termen der Form 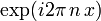 , mit
, mit 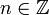 , und 0 in den anderen Fällen, aufgespannte Raum. Der Kern des adjungierten Operators ist ein ähnlicher Raum, nur wird λ durch sein komplex-konjugiertes ersetzt. D hat damit Index 0. Dieses Beispiel zeigt, dass Kern und Ko-Kern eines elliptischen Operators unstetig springen können falls man den elliptischen Operator so variiert, dass die oben erwähnten Terme erfasst werden. Es gibt also keine schöne Formel, die ihre Dimensionen durch topologische Größen ausdrückt.
, und 0 in den anderen Fällen, aufgespannte Raum. Der Kern des adjungierten Operators ist ein ähnlicher Raum, nur wird λ durch sein komplex-konjugiertes ersetzt. D hat damit Index 0. Dieses Beispiel zeigt, dass Kern und Ko-Kern eines elliptischen Operators unstetig springen können falls man den elliptischen Operator so variiert, dass die oben erwähnten Terme erfasst werden. Es gibt also keine schöne Formel, die ihre Dimensionen durch topologische Größen ausdrückt.Da die Sprünge in den Dimensionen von Kern und Ko-Kern aber gleich sind, ändert sich ihre Differenz, der Index, stetig und kann im Indexsatz durch topologische Größen ausgedrückt werden.
Topologischer Index
Der topologische Index eines elliptischen Differentialoperators D zwischen glatten Vektorbündeln E und F auf einer n-dimensionalen kompakten Mannigfaltigkeit X ist durch
- ch(D)Td(X)[X],
gegeben, dem Wert der höchstdimensionalen Komponente der gemischten Kohomologieklasse (mixed cohomology class) ch(D)Td(X) auf der fundamentalen Homologieklasse von X. Dabei ist
- Td(X) die Todd-Klasse auf X. Ferner ist
- ch(D) gleich φ−1(ch(d(E,F, σ(D)), mit folgenden Größen:
- φ, dem Thom-Isomorphismus von Hk(X,Q) nach Hn+k(B(X)/S(X),Q)
- B(X), dem Einheitsball-Bündel des Kotangenten-Bündels von X, und dessen Rand S(X) sowie der Projektion auf X, p .
Schließlich sind
- ch der Chern-Charakter der K-Theorie K(X) auf dem rationalen Kohomologiering H(X,Q) und
- d(p*E,p*F, σ(D)) das Differenz-Element ( "difference element") von K(B(X)/S(X)) zu zwei Vektorbündeln p*E und p*F auf B(X) und einem Isomorphismus σ(D) zwischen ihnen auf dem Unterraum S(X), und
- σ(D) das Symbol von D .
Eine andere Methode der Definition des topologischen Index nutzt systematisch die K-Theorie. Wenn X eine kompakte Untermannigfaltigkeit von Y ist gibt es eine pushforward-Operation von K(TX) nach K(TY). Der topologische Index eines Elements von K(TX) ist als Bild dieser Operation definiert, wobei Y ein euklidischer Raum ist, für den K(TY) auf natürliche Weise mit den ganzen Zahlen Z identifiziert werden kann. Der Index ist unabhängig von der Einbettung von X in den euklidischen Raum.
Der Atiyah-Singer-Indexsatz
D sei wieder ein elliptischer Differentialoperator zwischen zwei Vektorbündeln E und F über einer kompakten Mannigfaltigkeit X.
Das Index-Problem besteht in folgender Aufgabe: Zu berechnen ist der analytische Index von D einzig unter Benutzung der Symbole und von topologischen Invarianten der Mannigfaltigkeit und der Vektorbündel. Der Atiyah-Singer Indexsatz löst dieses Problem und besagt:
- Der analytische Index von D ist gleich dem topologischen Index.
Trotz seiner komplexen Formulierung kann der topologische Index im Allgemeinen gut berechnet werden, im Gegensatz zum analytischen Index[4]. Viele wichtige Invarianten der Mannigfaltigkeit (wie die Signatur) können als Index bestimmter Differentialoperatoren und damit durch topologische Größen ausgedrückt werden.
Obwohl der analytische Index schwer zu berechnen ist, ist er zumindest eine ganze Zahl, während der topologische Index nach Definition eine rationale Zahl ist und die „Ganzheit“ keineswegs offensichtlich ist. Der Indexsatz macht so auch für die Topologie tiefliegende Aussagen.
Der Index eines elliptischen Operators verschwindet offensichtlich falls der Operator selbstadjungiert ist. Er verschwindet auch bei Mannigfaltigkeiten X ungerader Dimension, es gibt aber auch elliptische Pseudodifferentialoperatoren, deren Index nicht in ungeraden Dimensionen verschwindet.
Beispiele
Die Euler-Poincaré-Charakteristik
X sei kompakt und orientierbar. E sei die Summe der geraden äußeren Produkte des Kotangenten-Bündels, F die Summe der ungeraden äußeren Produkte, D sei d + d*, eine Abbildung von E nach F. Dann ist der topologische Index von D die Euler-Poincaré-Charakteristik von M und der analytische Index ist die alternierende Summe der Dimensionen der de Rham-Kohomologiegruppen.
Das Theorem von Hirzebruch-Riemann-Roch
X sei eine komplexe Mannigfaltigkeit mit einem komplexen Vektorbündel V. Die Vektorbündel E und F seien die Summe der Bündel der Differentialformen mit Koeffizienten in V vom Typ (0,i), wobei i gerade oder ungerade ist. Der Differentialoperator D sei die Summe
eingeschränkt auf E (Dolbeault-Operator). Dann ist der analytische Index von D die holomorphe Euler-Poincaré-Charakteristik von V:
- index(D) = Σ(−1)p dim Hp(X,V)
Der topologische Index von D ist durch
- index(D) = ch(V)Td(X)[X],
gegeben als Produkt des Chern-Charakters von V und der Todd-Klasse von X, berechnet auf der Fundamentalklasse von X.
Gleichsetzung von topologischem und analytischem Index liefert das Hirzebruch-Riemann-Roch Theorem, das den Satz von Riemann-Roch verallgemeinert. Tatsächlich bewies Hirzebruch den Satz nur für projektive komplexe Mannigfaltigkeiten X, in obiger Form gilt er allgemein für komplexe Mannigfaltigkeiten.
Diese Ableitung des Hirzebruch-Riemann-Roch Theorems kann auch „natürlicher“ unter Verwendung des Indextheorems für elliptische Komplexe statt für elliptische Operatoren abgeleitet werden. Der Komplex sei
- 0→V→V⊗Λ0,1T*(X)→V⊗Λ0,2T*(X)...
mit dem Differential
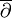 . Dann ist die ite Kohomologiegruppe gerade die kohärente Kohomologiegruppe Hi(X, V), so dass der analytische Index dieses Komplexes die holomorphe Euler-Charakteristik Σ (−1)i dim(Hi(X, V)) ist. Wie zuvor ist der topologische Index ch(W)Td(X)[X].
. Dann ist die ite Kohomologiegruppe gerade die kohärente Kohomologiegruppe Hi(X, V), so dass der analytische Index dieses Komplexes die holomorphe Euler-Charakteristik Σ (−1)i dim(Hi(X, V)) ist. Wie zuvor ist der topologische Index ch(W)Td(X)[X].Hirzebruchs Signatur-Satz
Der Signatur-Satz von Hirzebruch besagt, dass die Signatur einer kompakten glatten Mannigfaltigkeit X der Dimension 4k durch das L-Geschlecht von X gegeben ist. Das folgt aus dem Atiyah-Singer-Indexsatz angewandt auf folgenden Signatur-Operator.
Die Bündel E und F sind durch die +1- und −1-Eigenräume des Operators auf dem Bündel der Differentialformen von X gegeben. Er operiert auf den k-Formen als
- ik(k−1)
multipliziert mit dem *-Operator (Hodge-Dualitätsoperator). Der Operator D ist
- d + d*
eingeschränkt auf E, wobei d die äußere Ableitung nach Cartan und d* ihre adjungierte ist.
Der analytische Index von D ist die Signatur der Mannigfaltigkeit X, und ihr topologischer Index ist das L-Geschlecht von X, folglich sind beide gleich.
Das Â-Geschlecht und der Satz von Rochlin
Das Â-Geschlecht ist eine rationale Zahl definiert für eine beliebige Mannigfaltigkeit, aber im Allgemeinen keine ganze Zahl. Armand Borel und Friedrich Hirzebruch zeigten, dass sie für Spin-Mannigfaltigkeiten ganz ist und gerade, falls zusätzlich die Dimension gleich 4 mod 8 ist. Das lässt sich aus dem Indexsatz folgern, der dem Â-Geschlecht für Spin-Mannigfaltigkeiten den Index eines Diracoperators zuweist. Der Extrafaktor 2 in den Dimensionen, die mod 8 vier ergeben, kommt von der quaternionischen Struktur von Kern und Ko-Kern des Diracoperators in diesen Fällen. Als komplexe Vektorräume haben sie somit gerade Dimension, also ist auch der Index gerade.
In der Dimension 4 folgt daraus der Satz von Rochlin, dass die Signatur einer 4 dimensionalen Spin-Mannigfaltigkeit durch 16 teilbar ist, da dort die Signatur gleich dem (-8)-fachen des Â-Geschlechts ist.
Geschichte
Das Indexproblem für elliptische Differentialoperatoren wurde 1959 von Israel Gelfand (On Elliptic Equations, in den Russian Mathematical Surveys, 1960) gestellt. Er bemerkte die Homotopieinvarianz des Index und fragte nach einer Formel für den Index, die nur topologische Invarianten enthält. Weitere Motivationen für den Indexsatz waren das Riemann-Roch-Theorem und seine Verallgemeinerung das Hirzebruch-Riemann-Roch-Theorem sowie der Hirzebruch-Signatursatz. Hirzebruch und Borel hatten wie erwähnt die Ganzzahligkeit des Â-Geschlechts einer Spin-Mannigfaltigkeit bewiesen, und Atiyah schlug vor, dass dies erklärt werden könnte, falls es der Index eines Diracoperators wäre, der in der Mathematik 1961 von Atiyah und Singer „wiederentdeckt“ wurde.
Die erste Ankündigung wurde 1963 publiziert, der dort skizzierte Beweis wurde aber nie publiziert (erschien aber in dem Sammelband von Palais). Der erste veröffentlichte Beweis benutzte statt Kobordismus-Theorie die K-Theorie, die auch für die folgenden Beweise diverser Verallgemeinerungen benutzt wurde.
1973 gaben Atiyah, Raoul Bott und Patodi einen neuen Beweis mit Hilfe der Wärmeleitungsgleichung (Diffusionsgleichung).
1983 gab Ezra Getzler, nach Ideen von Edward Witten und Luis Alvarez-Gaume, einen kurzen Beweis des lokalen Indextheorems für Operatoren, die lokal Diracoperatoren sind (was die meisten Standardfälle umfasst).
Beweistechniken
Pseudodifferentialoperatoren
Während z.B. Differentialoperatoren mit konstanten Koeffizienten im euklidischen Raum Fouriertransformationen der Multiplikationen mit Polynomen sind, sind die entsprechenden Pseudodifferentialoperatoren Fouriertransformationen der Multiplikation mit allgemeineren Funktionen. Viele Beweise des Indexsatzes benutzen solche Pseudodifferentialoperatoren, da es für viele Zwecke „nicht genug“ Differentialoperatoren gibt. Beispielsweise ist die Pseudoinverse eines elliptischen Differentialoperators fast nie ein Differentialoperator, wohl aber ein Pseudodifferentialoperator. Für die meisten Versionen des Indexsatzes gibt es so eine Erweiterung auf Pseudodifferentialoperatoren. Die Beweise werden durch die Verwendung dieser verallgemeinerten Differentialoperatoren flexibler.
Kobordismus
Der ursprüngliche Beweis basierte wie der des Hirzebruch-Riemann-Roch-Theorems durch Hirzebruch 1954 auf der Verwendung der Kobordismentheorie und benutzte außerdem Pseudodifferentialoperatoren.
Die Idee des Beweises war grob wie folgt: Man betrachte den durch die Paare (X,V) erzeugten Ring, wo V ein glattes Vektorbündel auf einer glatten, kompakten, orientierbaren Mannigfaltigkeit X ist. Die Summe und das Produkt in diesem Ring sei durch die disjunkte Vereinigung und das Produkt von Mannigfaltigkeiten gegeben (mit entsprechenden Operationen auf den Vektorbündeln). Jede Mannigfaltigkeit, die Rand einer Mannigfaltigkeit ist, verschwindet. Das Vorgehen ist wie in der Kobordismentheorie, nur dass hier die Mannigfaltigkeiten auch Vektorbündel tragen. Analytischer und Topologischer Index werden als Funktionen auf diesem Ring mit Werten in den ganzen Zahlen interpretiert. Nachdem man überprüft hat, ob die so interpretierten Indices Ring-Homomorphismen sind, muss man ihre Gleichheit nur noch für die Generatoren des Rings beweisen. Diese ergeben sich aus Rene Thoms Kobordismentheorie, z.B. komplexe Vektorräume mit dem trivialen Bündel und bestimmte Bündel über Sphären gerader Dimension. Der Indexsatz muss damit nur noch auf relativ einfachen Mannigfaltigkeiten betrachtet werden.
K-Theorie
Der erste veröffentlichte Beweis von Atiyah und Singer nutzte K-Theorie statt Kobordismen. Sei i eine beliebige Inklusion kompakter Mannigfaltigkeiten von X nach Y. Dann kann man eine pushforward Operation i! von elliptischen Operatoren auf X nach elliptischen Operatoren auf Y definieren, die den Index erhält. Nimmt man Y als in X eingebettete Sphäre reduziert sich der Indexsatz auf den Fall von Sphären. Falls Y eine Sphäre ist und X ein in Y eingebetteter Punkt, dann ist jeder elliptische Operator auf Y unter i! das Bild eines elliptischen Operators auf dem Punkt. Das reduziert den Indexsatz auf den Fall eines Punktes, wo er trivial ist.
Wärmeleitungsgleichung
Atiyah, Raoul Bott und Vijay Kumar Patodi gaben einen neuen Beweis des Indexsatzes unter Verwendung der Wärmeleitungsgleichung
Wenn D ein Differentialoperator mit Adjungierter D* ist, sind D*D und DD* selbstadjungierter Operatoren, deren nicht verschwindende Eigenwerte dieselbe Vielfachheit besitzen. Ihre Eigenräume zum Eigenwert null können aber verschiedene Vielfachheit besitzen, da diese die Dimensionen der Kerne von D und D* sind. Der Index von D ist daher durch
- Index(D) = dim Ker(D) − dim Ker(D*) = Tr(e−tD*D) − Tr(e−tDD*)
gegeben, für beliebige positive t. Die rechte Seite der Gleichung ist durch die Spur der Differenz der Kerne von zwei Wärmeleitungsoperatoren gegeben. Ihre asymptotische Entwicklung für kleine positive t kann genutzt werden, um den Grenzwert t gegen 0 zu bestimmen und so einen Beweis des Atiyah-Singer-Indexsatzes zu liefern. Der Grenzwert kleiner t ist auf den ersten Blick ziemlich kompliziert, da sich aber viele der Terme aufheben können die führenden Terme explizit angegeben werden. Der tiefere Grund dafür, dass sich viele der Terme aufheben, wurde später durch die Supersymmetrie geliefert.
Verallgemeinerungen
- Statt mit elliptischen Operatoren zwischen Vektorbündeln, ist es manchmal vorteilhafter mit einem elliptischen Komplex von Vektorbündeln zu arbeiten:
-
- 0 → E0 → E1 →E2 → ... → Em →0
Der Unterschied liegt darin, dass die Symbole nun eine exakte Sequenz bilden (außerhalb der Null-Sektion). Im Fall von genau zwei Bündeln (ungleich Null) im Komplex folgt daraus, dass das Symbol außerhalb des Null-Schnittes ein Isomorphismus ist, so dass ein elliptischer Komplex mit 2 Termen im Wesentlichen das gleiche wie ein elliptischer Operator zwischen zwei Vektorbündeln ist. Umgekehrt kann der Indexsatz eines elliptischen Komplexes leicht auf den Indexsatz eines elliptischen Operators reduziert werden. Die beiden Vektorbündel sind durch die Summe der geraden oder ungeraden Terme im Komplex gegeben, und der elliptische Operator ist die Summe der Operatoren des elliptischen Komplexes und seiner Adjungierten, eingeschränkt auf die Summe der geraden Bündel.
- Hat die Mannigfaltigkeit einen Rand, muss das Definitionsgebiet des elliptischen Operators eingeschränkt werden um einen endlichen Index sicherzustellen. Diese Zusatzbedingungen können lokal sein und das Verschwinden der Schnitte (der Vektorbündel) auf dem Rand fordern, oder komplexere globale Bedingungen, die z.B. das Erfüllen bestimmter Differentialgleichungen durch die Schnitte fordern. Atiyah und Bott untersuchten den lokalen Fall, zeigten aber auch, dass viele interessante Operatoren wie der Signaturoperator keine lokalen Randbedingungen erlauben. Atiyah, Patodi und Singer führten für diese Fälle globale Randbedingungen ein, die dem Anhängen eines Zylinders an den Rand der Mannigfaltigkeit entsprechen und den Definitionsbereich auf solche Schnitte einschränkten, die entlang des Zylinders quadratintegrabel sind. Die Sichtweise wurde von Melrose in seinem Beweis des Atiyah-Patodi-Singer-Indexsatzes verwendet.
- Statt eines elliptischen Operators kann man ganze Familien betrachten, parametrisiert durch einen Raum Y. In diesem Fall ist der Index ein Element der K-Theorie von Y statt einer ganzen Zahl. Sind die Operatoren reell, ist der Index in der reellen K-Theorie von Y, was gegenüber der komplexen K-Theorie manchmal einige Zusatzinformationen über die Mannigfaltigkeit liefert.
- Gibt es eine auf der kompakten Mannigfaltigkeit X erklärte Wirkung einer Gruppe G, die mit dem elliptischen Operator kommutiert, wird die gewöhnliche K-Theorie durch Äquivariante K-Theorie ersetzt (Atiyah, Bott). Man erhält hier Verallgemeinerungen des Lefschetz-Fixpunktsatzes, wobei die Fixpunkte sich auf die unter G invarianten Untermannigfaltigkeiten beziehen.
- Atiyah zeigte auch, wie man den Indexsatz auf einige nicht-kompakte Mannigfaltigkeiten erweitern kann, falls auf ihnen diskrete Gruppen mit kompaktem Quotienten operieren. Der Kern des elliptischen Operators ist in diesem Fall meist unendlich dimensional, aber man kann einen endlichen Index unter Benutzung der Dimension eines Moduls über einer Von-Neumann-Algebra erhalten. Im Allgemeinen ist dieser Index reell statt ganzzahlig. Dieses L2-Indextheorem wurde von Atiyah und Wilfried Schmid dazu benutzt, Sätze über die diskreten Serien in der Darstellungstheorie halbeinfacher Liegruppen neu abzuleiten (Astérisque Bd. 32, Nr.3, 1976, S. 43-72).
Zitate
"Wissenschaftler beschreiben die Welt durch Größen und Kräfte, die in Raum und Zeit veränderlich sind. Die Naturgesetze werden oft durch Formeln für deren Veränderungsrate ausgedrückt, Differentialgleichungen genannt. Solche Formeln können einen „Index“ haben, die Zahl der Lösungen der Formeln minus der Zahl der Beschränkungen, die diese den zu berechnenden Grössen auferlegen. Der Atiyah-Singer-Indexsatz berechnet diesen Index aus der Geometrie des zugrundeliegenden Raumes. Ein einfaches Beispiel liefert M.C. Eschers berühmtes paradoxes Bild „Aufsteigen und Absteigen“, in dem die Leute zwar die ganze Zeit aufsteigen, sich aber dennoch im Kreis um den Schlosshof bewegen. Der Indexsatz hätte ihnen gesagt, dass das unmöglich ist."[5]
Literatur
- Israel Gelfand On elliptic equations, Russian Math.Surveys Bd.15, 1960, s.113 (oder Gelfand Collected works, Bd.1)
- Atiyah Collected works, Bd.3 (Abdruck der unten zitierten Arbeiten)
- Atiyah, Singer: The index of elliptic operators on compact manifolds, Bulletin American Mathematical Society Bd.69, 1963, S.322 (Ankündigung)
- dies.: The index of elliptic operators I Annals of Mathematics Bd.87, 1968, S.484 (Beweis mit K-Theorie)
- dies. The index of elliptic operators III, ibid. S.546 (Kohomologie statt K-Theorie)
- Atiyah, Graeme Segal: The index of elliptic operators II, ibid. S.531 (mit equivarianter K-Theorie als eine Art Lefschetz Fixpunktsatz)
- Atiyah, Singer The index of elliptic operators IV, Annals of Math. Bd.93, 1971, S.119 (mit Familien von Operatoren)
- dies. The index of elliptic operators V, ibid. S.139 (reelle statt komplexe Operatoren)
- Richard Palais (Hrsg.) Seminar on the Atiyah-Singer-Indextheorem, Princeton, Annals of Mathematical Studies Bd.57 (enthält Kobordismus Beweis)
- Atiyah, Bott A Lefschetz fixed point formula for elliptic complexes, Teil 1,2, Annals of Mathematics, Bd.86, 1967, S.374, Bd.88, 1968, S.451
- Ezra Getzler Pseudodifferential operators on supermanifolds and the Atiyah-Singer-Indextheorem, Communications Math.Physics, Bd.92, 1983, S.163
- ders. A short proof of the local Atiyah-Singer-Indextheorem, Topology Bd.25, 1988, S.111-117
- ders., Nicole Berline, Michèle Vergne Heat Kernels and Dirac Operators, Springer ISBN 3540200622 (Beweis mit Diffusionsgleichung und Supersymmetrie).
- J.Roe Elliptic operators, topology and asymptotic methods, Chapman and Hall 1999
- Bernhelm Booss Topologie und Analysis- Einführung in die Atiyah-Singer-Indexformel, Springer 1977
Weblinks
- Gilkey Invariance Theory, the Heat Equation, and the Atiyah–Singer Theorem, online Buch, Wärmeleitungsgleichungs-Methode, englisch
- Richard Melrose The Atiyah-Patodi-Singer Index Theorem, online Buch, englisch.
- Wassermann, Vorlesungen über das Indextheorem, englisch
- Interview mit Atiyah, Singer, Notices AMS 2005, pdf, englisch
Einzelnachweise
- ↑ Im Folgenden steht das Wort für den hier definierten technischen Ausdruck
- ↑ Im Allgemeinen transformieren Differentialoperatoren auf ziemliche komplizierte Weise bei Koordinatentransformationen, aber die Terme höchster Ordnung verhalten sich wie Tensoren, so dass wir hier wohldefinierte homogene Funktionen in den Kotangentialräumen erhalten, die unabhängig von den lokalen Karten sind
- ↑ Die Pseudoinverse eines elliptischen Differentialoperators ist fast nie ein Differentialoperator, aber ein elliptischer Pseudo-Differentialoperator.
- ↑ Kern und Ko-Kern sind im Allgemeinen sehr schwer zu berechnen, nach dem Indexsatz gibt es aber relativ einfache Formel für die Differenz der Dimensionen
- ↑ Aus der offiziellen Würdigung für Atiyah und Singer zum Abelpreis 2004.
Wikimedia Foundation.