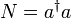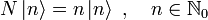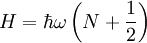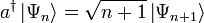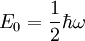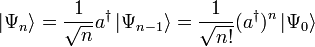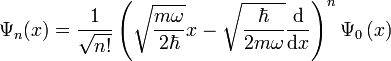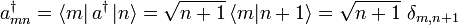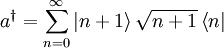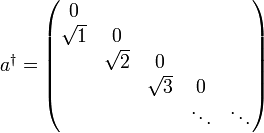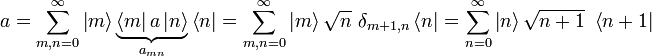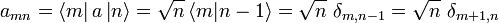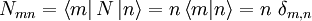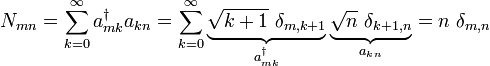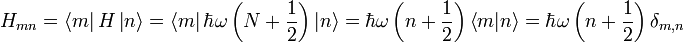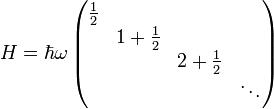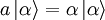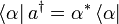- Auf- und Absteigeoperator
-
Die Erzeugungs- und Vernichtungsoperatoren sind der Kern einer eleganten Lösung der Schrödingergleichung des harmonischen Oszillators. Diese Operatoren können auch dazu benutzt werden, gewisse Probleme mit quantenmechanischem Drehimpuls einfacher zu lösen. Ferner finden die Erzeugungs- und Vernichtungsoperatoren Verwendung bei der Quantisierung von Feldern (der sogenannten zweiten Quantisierung oder Besetzungszahl-Darstellung).
Es gibt eine Vielzahl alternativer Bezeichnungen wie Leiteroperatoren, Kletteroperatoren, Aufsteige- und Absteigeoperatoren sowie Hebe- und Senkoperatoren. Statt „Erzeugungsoperator“ wird manchmal auch Erschaffungsoperator verwendet. Im deutschsprachigen Raum werden darüber hinaus auch die Operatoren σ + und σ − , die die Zustände eines Atoms ändern, als Erzeugungs- bzw. Vernichtungsoperatoren bezeichnet.
Das Problem des harmonischen Oszillators in der Quantenmechanik lässt sich mithilfe der Methode der Erzeugungs- und Vernichtungsoperatoren behandeln, die auch algebraische Methode genannt wird. Sie wurde hauptsächlich von Paul Dirac entwickelt. Für diesen Lösungsweg definiert man zwei Operatoren
 und
und 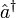 , die einem Oszillator jeweils ein Energiequant
, die einem Oszillator jeweils ein Energiequant 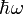 entziehen oder hinzufügen. Man nennt sie deswegen Vernichtungs- und Erzeugungsoperator
entziehen oder hinzufügen. Man nennt sie deswegen Vernichtungs- und ErzeugungsoperatorDas Zirkumflex über dem a symbolisiert, dass es sich dabei um einen Operator handelt. Damit gelten nicht dieselben Rechenregeln wie für Skalare, denn die Reihenfolge von Operatoren lässt sich beispielsweise im Allgemeinen nicht vertauschen. Im Folgenden wird auf das Zirkumflex zugunsten der Übersichtlichkeit verzichtet. Alle lateinischen Großbuchstaben, mit Ausnahme des E, sind Operatoren.
Inhaltsverzeichnis
Definition
Man definiert den Erzeugungsoperator
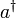 und den dazu adjungierten Vernichtungsoperator
und den dazu adjungierten Vernichtungsoperator 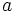 über folgende Vertauschungsrelationen mit dem Besetzungszahloperator
über folgende Vertauschungsrelationen mit dem Besetzungszahloperator 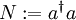 :
:Der Besetzungszahloperator N ist ein hermitescher Operator und hat daher reelle Eigenwerte n. Die zugehörige Eigenwertgleichung lautet, wobei
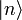 Fock-Zustände sind:
Fock-Zustände sind:Die Besetzungszahl n ist eine nichtnegative ganze Zahl, also
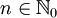 . Bei Fermionen ergibt sich hier noch eine Einschränkung auf die Werte 0 und 1.
. Bei Fermionen ergibt sich hier noch eine Einschränkung auf die Werte 0 und 1.Durch Anwendung von
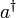 bzw. a auf den Zustand
bzw. a auf den Zustand 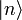 erhält man den darüber- bzw. den darunterliegenden Zustand:
erhält man den darüber- bzw. den darunterliegenden Zustand:Die Konstanten
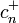 und
und  sind davon abhängig, ob a und
sind davon abhängig, ob a und 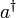 die Kommutator- oder Antikommutatior-Vertauschungsrelation erfüllen.
die Kommutator- oder Antikommutatior-Vertauschungsrelation erfüllen.Details
Im Folgenden werden verschiedene Eigenschaften von N abgeleitet. Die Eigenzustände
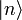 seien normiert.
seien normiert.- Der Besetzungszahloperator ist hermitesch, also selbstadjungiert:
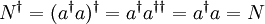
- Somit hat N reelle Eigenwerte, die Besetzungszahlen n.
- Die Eigenwerte sind nicht negativ:
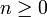
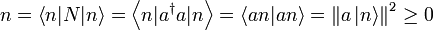
- Die Ungleichung folgt aus der Tatsache, dass die Norm eines Vektors nicht-negativ ist.
- Der kleinste Eigenwert ist 0
- Der Zustand
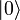 ist ein Vektor im Hilbertraum und darf nicht mit dem Nullvektor verwechselt werden, sondern wird lediglich mit der Zahl 0 nummeriert.
ist ein Vektor im Hilbertraum und darf nicht mit dem Nullvektor verwechselt werden, sondern wird lediglich mit der Zahl 0 nummeriert. 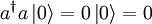 und
und 
- Wegen
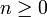 muss gelten:
muss gelten: 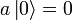 . Wendet man also auf den niedrigsten Zustand den Absteigeoperator an, so erhält man den Nullvektor. Dies lässt sich aber nicht umkehren: Durch Anwendung von
. Wendet man also auf den niedrigsten Zustand den Absteigeoperator an, so erhält man den Nullvektor. Dies lässt sich aber nicht umkehren: Durch Anwendung von 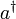 auf den Nullvektor erhält man nicht den Grundzustand sondern wieder den Nullvektor.
auf den Nullvektor erhält man nicht den Grundzustand sondern wieder den Nullvektor.
- Die Eigenwerte sind ganzzahlig:
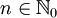
- Angenommen die Eigenwerte wären nicht ganzzahlig, so lassen sich ausgehend von einem Eigenzustand durch mehrmaliges Anwendung des Absteigeoperators Eigenzustände finden, die negative Eigenwerte besitzen. Dies ist aber ein Widerspruch zur Bedingung
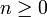 . Bei ganzzahligen Eigenwerten erreicht man irgendwann den Grundzustand und durch nochmaliges Anwenden den Nullvektor; ab hier bricht automatisch die Leiter ab.
. Bei ganzzahligen Eigenwerten erreicht man irgendwann den Grundzustand und durch nochmaliges Anwenden den Nullvektor; ab hier bricht automatisch die Leiter ab.
- Ist n Eigenwert, dann auch n + 1
![Na^{\dagger}\left|n\right\rangle =\left(a^{\dagger}N+[N,a^{\dagger}]\right)\left|n\right\rangle =\left(a^{\dagger}N+a^{\dagger}\right)\left|n\right\rangle =a^{\dagger}\left(N+1\right)\left|n\right\rangle =a^{\dagger}\left(n+1\right)\left|n\right\rangle =\left(n+1\right)a^{\dagger}\left|n\right\rangle](/pictures/dewiki/98/b9ce56974880bc7782bed2ab6698bd47.png)
- Wenn
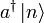 ungleich dem Nullvektor ist, erhält man somit einen neuen Eigenwert (n + 1).
ungleich dem Nullvektor ist, erhält man somit einen neuen Eigenwert (n + 1). 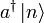 ist also Eigenzustand zu N mit Eigenwert (n + 1) und somit proportional zu
ist also Eigenzustand zu N mit Eigenwert (n + 1) und somit proportional zu 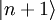 :
: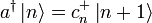
- Ist n > 0 Eigenwert, dann auch n − 1
![Na\left|n\right\rangle =\left(aN+\left[N,a\right]\right)\left|n\right\rangle =\left(aN-a\right)\left|n\right\rangle =a\left(N-1\right)\left|n\right\rangle =a\left(n-1\right)\left|n\right\rangle =\left(n-1\right)a\left|n\right\rangle](/pictures/dewiki/50/22b74c91d4809a8502d8c1cdd425f1e7.png)
- Wenn
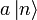 ungleich dem Nullvektor ist, erhält man somit einen neuen Eigenwert (n − 1)
ungleich dem Nullvektor ist, erhält man somit einen neuen Eigenwert (n − 1) 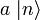 ist also Eigenzustand zu N mit Eigenwert (n − 1) und somit proportional zu
ist also Eigenzustand zu N mit Eigenwert (n − 1) und somit proportional zu 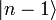 :
: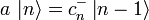
Bosonische Kletteroperatoren
Im bosonischen Fall erfüllen a und
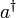 die Kommutator-Vertauschungsrelationen:
die Kommutator-Vertauschungsrelationen:Somit
Im bosonischen Fall können die Besetzungszahlen n beliebig groß werden:
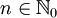 .
.Details
- Zunächst ist zu prüfen, ob die obigen Voraussetzungen erfüllt werden:
- Mit
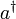 lässt sich der nächste über
lässt sich der nächste über 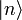 liegende Zustand konstruieren
liegende Zustand konstruieren 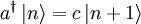 . Der Faktor c ergibt sich aus folgender Rechnung mit dem Kommutator
. Der Faktor c ergibt sich aus folgender Rechnung mit dem Kommutator 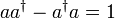 :
:
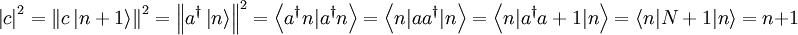
 , die Phase φ kann aber vernachlässigt werden, sodass
, die Phase φ kann aber vernachlässigt werden, sodass 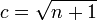 .
.
- Mit a lässt sich der unter
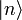 liegende Zustand konstruieren
liegende Zustand konstruieren 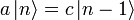 . Der Faktor c ergibt sich aus folgender Rechnung:
. Der Faktor c ergibt sich aus folgender Rechnung:
- Alle Eigenzustände lassen sich vom Grundzustand ausgehend konstruieren:
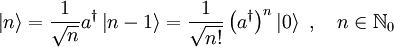
- Auf diese Weise erhält man einen vollständigen diskreten Satz von Eigenzuständen
Fermionische Kletteroperatoren
Im fermionischen Fall erfüllen a und
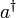 die Anti-Kommutator-Vertauschungsrelationen:
die Anti-Kommutator-Vertauschungsrelationen:Somit
Im fermionischen Fall können die Besetzungszahlen n nur die Werte 0 oder 1 annehmen.
Details
- Mit
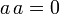 und
und  ist N2 = N:
ist N2 = N:
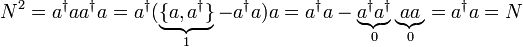
- Der Besetzungszahloperator hat also nur die Eigenwerte 0 und 1 und die Eigenzustände
 und
und 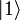 :
: 
- Zunächst ist zu prüfen, ob die obigen Voraussetzungen erfüllt werden:
- Mit
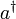 lässt sich der nächste über
lässt sich der nächste über 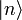 liegende Zustand konstruieren
liegende Zustand konstruieren 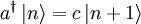 . Der Faktor c ergibt sich aus folgender Rechnung mit dem Anti-Kommutator
. Der Faktor c ergibt sich aus folgender Rechnung mit dem Anti-Kommutator 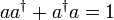 :
:
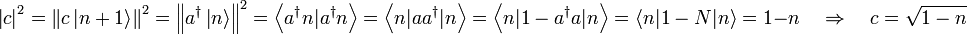
- Da n nur 0 oder 1 sein kann, ist
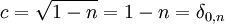 (dabei ist δi,j das Kronecker-Delta).
(dabei ist δi,j das Kronecker-Delta).
- Mit a lässt sich der unter
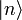 liegende Zustand konstruieren
liegende Zustand konstruieren 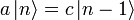 . Der Faktor c ergibt sich aus folgender Rechnung:
. Der Faktor c ergibt sich aus folgender Rechnung:
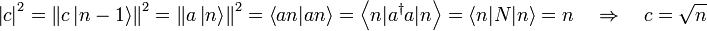
- Da n nur 0 oder 1 sein kann, ist
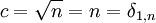 .
.
- Alle Eigenzustände lassen sich vom Grundzustand ausgehend konstruieren:
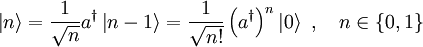
- Auf diese Weise erhält man einen vollständigen diskreten Satz von Eigenzuständen
Beispiel für bosonische Kletteroperatoren: Harmonischer Oszillator
Der Hamiltonoperator H des harmonischen Oszillators lautet
P Impulsoperator, Q Ortsoperator, m Masse, ω Eigenfrequenz
Im Folgenden ist die stationäre Schrödingergleichung zu lösen:
En Energieeigenwert,
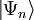 Energieeigenzustand
EnergieeigenzustandHamiltonoperator umformen
Der Hamiltonoperator lässt sich umformen:
Es werden zwei neue Operatoren definiert:
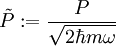 und
und 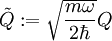
Der Hamiltonoperator ausgedrückt mit den neuen Operatoren:
Man versucht nun, den Inhalt der Klammer als Produkt zu schreiben, also (i ist die imaginäre Einheit)
Da aber u und v Operatoren sind, die nicht vertauschen, gilt hier das letzte Gleichheitszeichen nicht. Um zwei Operatoren miteinander zu vertauschen, ist der Kommutator vonnöten:
![\tilde{Q}\tilde{P}=\tilde{P}\tilde{Q}-\left[ \tilde{P},\tilde{Q} \right]](/pictures/dewiki/97/a27d96413b9c979d89f451c2b2072cec.png)
Der Kommutator
![\left[ \tilde{Q},\tilde{P} \right]](/pictures/dewiki/102/fafc0ccc8db8a10afbbe4d3a32b2ba56.png) kann auf den Kommutator der ursprünglichen Operatoren Q und P zurückgeführt werden:
kann auf den Kommutator der ursprünglichen Operatoren Q und P zurückgeführt werden:Der Hamiltonoperator sieht nun folgendermaßen aus:
Jetzt werden die beiden Leiteroperatoren definiert:
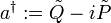 Erzeugungsoperator
Erzeugungsoperator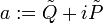 Vernichtungsoperator
Vernichtungsoperator
Häufig werden sie auch als a+ und a- geschrieben. Man beachte, dass die Leiteroperatoren nicht hermitesch sind, da
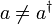 .
.Die Leiteroperatoren ausgedrückt durch Ortsoperator Q und Impulsoperator P:
Mit den Leiteroperatoren schreibt sich der Hamiltonoperator:
Eigenschaften der Erzeuger und Vernichter
Zu bestimmen ist noch der Kommutator aus den beiden Leiteroperatoren:
Da außerdem
![[a,a]=[a^{\dagger},a^{\dagger}]=0](/pictures/dewiki/97/a6508c240ed420c24d2a75e7407a9431.png) gilt, handelt es sich bei den Kletteroperatoren des harmonischen Oszillators um bosonische Kletteroperatoren. Somit gelten alle obigen Eigenschaften für bosonische Kletteroperatoren.
gilt, handelt es sich bei den Kletteroperatoren des harmonischen Oszillators um bosonische Kletteroperatoren. Somit gelten alle obigen Eigenschaften für bosonische Kletteroperatoren.Das Produkt
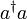 definiert den Besetzungszahloperator:
definiert den Besetzungszahloperator:Der Besetzungszahloperator N ist ein hermitescher Operator und hat daher reelle Eigenwerte, die Besetzungszahlen n. Die Eigenzustände sind Fock-Zustände oder Besetzungszahlzustände. Die zugehörige Eigenwertgleichung lautet:
Lösung des Eigenwertproblems
Der Hamiltonoperator lässt sich durch den Besetzungszahloperator ausdrücken:
Das Eigenwertproblem
 lässt sich auf die Eigenwertgleichung des Besetzungszahloperators
lässt sich auf die Eigenwertgleichung des Besetzungszahloperators 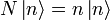 zurückführen.
zurückführen.Die Eigenzustände von N sind auch Eigenzustände von H, da
![\left[ H,N \right]=0](/pictures/dewiki/56/814a91ce2c6f3d1c9f3ccd174d434fbb.png) . Die Eigenwerte des Hamiltonoperators ergeben sich aus den Eigenwerten des Besetzungszahloperators N:
. Die Eigenwerte des Hamiltonoperators ergeben sich aus den Eigenwerten des Besetzungszahloperators N: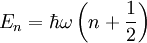 und
und 
Eine besonders wichtige Eigenschaft der Kletteroperatoren ist diese:
Ist
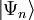 eine Lösung der Schrödingergleichung für die Energie En, so ist
eine Lösung der Schrödingergleichung für die Energie En, so ist 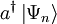 eine Lösung für die Energie
eine Lösung für die Energie  und
und 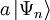 eine Lösung für die Energie
eine Lösung für die Energie 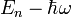 . Das bedeutet, dass man aus einer Lösung alle Lösungen erhalten kann, indem man einfach den Erzeugungs- oder Vernichtungsoperator auf diese Lösung anwendet. Dadurch wird eine neue Lösung für das benachbarte Energieniveau erzeugt, das um die Energie
. Das bedeutet, dass man aus einer Lösung alle Lösungen erhalten kann, indem man einfach den Erzeugungs- oder Vernichtungsoperator auf diese Lösung anwendet. Dadurch wird eine neue Lösung für das benachbarte Energieniveau erzeugt, das um die Energie 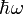 verschoben ist.
verschoben ist.Da der Besetzungszahloperator keine negativen Eigenwerte hat, können auch keine negativen Energieeigenwerte existieren. Es gibt also für die minimale Besetzungszahl n = 0 eine Lösung
 , die auf einem minimalen Energieniveau sitzt (Nullpunktsenergie):
, die auf einem minimalen Energieniveau sitzt (Nullpunktsenergie):Im Zustand
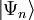 setzt sich die Energie
setzt sich die Energie 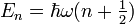 zusammen aus der Nullpunktsenergie
zusammen aus der Nullpunktsenergie 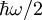 und n Energiequanten der Größe
und n Energiequanten der Größe 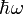 . Die Wirkung von
. Die Wirkung von 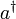 überführt das System in einen Zustand mit der um
überführt das System in einen Zustand mit der um 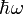 erhöhten Energie. Dies kann man als Erzeugung eines zusätzlichen Energiequants interpretieren, was den Namen Erzeugungsoperator verständlich macht. Analog überführt der Operator a das System in einen um ein Energiequant reduzierten Zustand. Es wird also ein Energiequant vernichtet, deswegen Vernichtungsoperator. Die Eigenwerte des Operators N geben an, wieviele Energiequanten in einem Eigenzustand angeregt sind. Die Besetzung eines Zustandes mit n Energiequanten erklärt den Namen Besetzungszahloperator.
erhöhten Energie. Dies kann man als Erzeugung eines zusätzlichen Energiequants interpretieren, was den Namen Erzeugungsoperator verständlich macht. Analog überführt der Operator a das System in einen um ein Energiequant reduzierten Zustand. Es wird also ein Energiequant vernichtet, deswegen Vernichtungsoperator. Die Eigenwerte des Operators N geben an, wieviele Energiequanten in einem Eigenzustand angeregt sind. Die Besetzung eines Zustandes mit n Energiequanten erklärt den Namen Besetzungszahloperator.Eigenfunktionen in Ortsdarstellung
Wendet man also auf den niedrigsten Zustand den Absteigeoperator an, so erhält man den Nullvektor
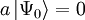 . Dies lässt sich aber nicht umkehren: Durch Anwendung von
. Dies lässt sich aber nicht umkehren: Durch Anwendung von 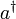 auf den Nullvektor erhält man nicht den Grundzustand sondern wieder den Nullvektor
auf den Nullvektor erhält man nicht den Grundzustand sondern wieder den Nullvektor 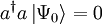 . Dies liefert eine Gleichung für den Grundzustand:
. Dies liefert eine Gleichung für den Grundzustand:In der Ortsdarstellung kann man obige Operatorgleichung als Differentialgleichung darstellen und lösen:
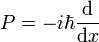 und Q = x
und Q = x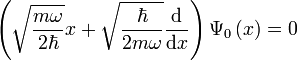 liefert normiert
liefert normiert 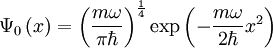
Durch Anwendung des Aufsteigeoperators auf die Lösung des Grundzustands erhält man alle höheren Eigenfunktionen:
In Ortsdarstellung erhält man somit:
Matrixdarstellung bosonischer Kletteroperatoren
Die Eigenzustände des Besetzungszahloperators
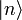 bilden ein vollständiges Orthonormalsystem. Mit Hilfe dieser Hilbertraumbasis soll nun eine Matrixdarstellung der Leiteroperatoren ermittelt werden. Man beachte, dass hier alle Indizes von 0 (nicht von 1) bis unendlich laufen. Die Eigenzustände lassen sich als Vektoren darstellen:
bilden ein vollständiges Orthonormalsystem. Mit Hilfe dieser Hilbertraumbasis soll nun eine Matrixdarstellung der Leiteroperatoren ermittelt werden. Man beachte, dass hier alle Indizes von 0 (nicht von 1) bis unendlich laufen. Die Eigenzustände lassen sich als Vektoren darstellen: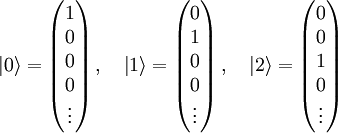 usw.
usw.
Die Vollständigkeit dieser Basis liefert eine Darstellung des Einheitsoperators:
Erzeugungsoperator
Vor und nach dem Erzeugungsoperator wird eine 1 (Einheitsoperator) eingeschoben:
Das Matrixelement berechnet sich zu
Der Erzeugungsoperator dargestellt durch die Basisvektoren
Somit ergibt sich die Matrixdarstellung des Erzeugungsoperators bzgl. der Besetzungseigenbasis (alle nicht angegebenen Elemente sind gleich 0):
Vernichtungsoperator
Durch analoge Rechnung erhält man für den Vernichtungsoperator:
Dabei wurde das Matrixelement schon eingesetzt:
Matrixdarstellung des Vernichtungsoperators bzgl. der Besetzungseigenbasis:
Man erkennt, dass die Matrix
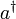 genau die transponierte von a ist. Dies ist verständlich, da die beiden Operatoren zueinander adjungiert (= transponiert + komplex konjugiert) sind.
genau die transponierte von a ist. Dies ist verständlich, da die beiden Operatoren zueinander adjungiert (= transponiert + komplex konjugiert) sind.Besetzungszahloperator
Matrixelement des Besetzungszahloperators bzgl. der Besetzungseigenbasis:
alternativ mit den Leiteroperatoren:
Matrixdarstellung des Besetzungszahloperators bzgl. der Besetzungseigenbasis:
Hamiltonoperator des harmonischen Oszillators
Matrixelement des Hamiltonoperators für den harmonischen Oszillator bzgl. der Besetzungseigenbasis bzw. der Energieeigenbasis:
Matrixdarstellung des Hamiltonoperators für den harmonischen Oszillator bzgl. der Besetzungseigenbasis bzw. der Energieeigenbasis:
Da die Operatoren N und H hermitesch sind, folgt dass die zugehörigen Matrizen bzgl. der Eigenbasen symmetrisch sind.
Eigenzustände bosonischer Kletteroperatoren
Die Eigenzustände des Vernichtungsoperators sind die kohärenten Zustände
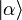 . Der Vernichtungsoperator a erfüllt folgende Eigenwertgleichung:
. Der Vernichtungsoperator a erfüllt folgende Eigenwertgleichung:Der Erzeugungsoperator erfüllt folgende Eigenwertgleichung, mit einem Linkseigenzustand (Bra-Eigenzustand):
Der Vernichtungsoperator a kann im Gegensatz zum Erzeugungsoperator
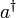 Rechtseigenzustände (Ket-Eigenzustände) besitzen. Der Erzeugungsoperator erhöht die minimale Teilchenzahl eines Zustandes im Fockraum um eins; der damit entstandene Zustand kann also nicht der ursprüngliche sein. Dagegen verringert der Vernichtungsoperator die maximale Teilchenzahl um eins; da ein Zustand im Fockraum aber Komponenten aller Teilchenzahlen (auch beliebig hoher Teilchenzahlen) beinhalten kann, ist damit nicht verboten, dass a Eigenzustände besitzt. Dies sind die kohärenten Zustände.
Rechtseigenzustände (Ket-Eigenzustände) besitzen. Der Erzeugungsoperator erhöht die minimale Teilchenzahl eines Zustandes im Fockraum um eins; der damit entstandene Zustand kann also nicht der ursprüngliche sein. Dagegen verringert der Vernichtungsoperator die maximale Teilchenzahl um eins; da ein Zustand im Fockraum aber Komponenten aller Teilchenzahlen (auch beliebig hoher Teilchenzahlen) beinhalten kann, ist damit nicht verboten, dass a Eigenzustände besitzt. Dies sind die kohärenten Zustände.Der kohärente Zustand
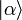 ergibt sich als Linearkombination von allen Zuständen fester Teilchenzahl
ergibt sich als Linearkombination von allen Zuständen fester Teilchenzahl 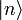 nach:
nach:Dabei ist α eine nichtverschwindende komplexe Zahl, die den kohärenten Zustand vollständig definiert.
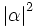 ist der Erwartungswert der Besetzungszahl des kohärenten Zustandes. Kohärente Zustände haben minimale Unschärfe und bleiben bei Zeitentwicklung kohärent. Mit ihnen lässt sich die elektromagnetische Welle einer Laser-Mode am besten beschreiben.
ist der Erwartungswert der Besetzungszahl des kohärenten Zustandes. Kohärente Zustände haben minimale Unschärfe und bleiben bei Zeitentwicklung kohärent. Mit ihnen lässt sich die elektromagnetische Welle einer Laser-Mode am besten beschreiben.Literatur
- Cohen-Tannoudji, Diu, Laloe: Quantenmechanik 1/2. de Gruyter, Berlin
- Nolting: Grundkurs theoretische Physik. Bd.5/1 : Quantenmechanik. Springer, Berlin
Siehe auch
Wikimedia Foundation.

![[N,a]=-a\ ,\quad[N,a^{\dagger}]=a^{\dagger}](/pictures/dewiki/50/207e33c14963149a693bf188c968dd42.png)
![[a,a^{\dagger}]=1\ ,\quad[a,a]=[a^{\dagger},a^{\dagger}]=0](/pictures/dewiki/54/6690d663a85050d2a0be5c651864eeea.png)

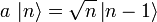
![[N,a]=[a^{\dagger}a,a]=\underbrace{[a^{\dagger},a]}_{-1}a+a^{\dagger}\underbrace{[a,a]}_{0}=-a](/pictures/dewiki/49/1f1d82030b9dd5b02ebdc9be2aa9e0e6.png)
![[N,a^{\dagger}]=[a^{\dagger}a,a^{\dagger}]=\underbrace{[a^{\dagger},a^{\dagger}]}_{0}a+a^{\dagger}\underbrace{[a,a^{\dagger}]}_{1}=a^{\dagger}](/pictures/dewiki/102/fb5aa76c01275d359da82a6450f306f4.png)
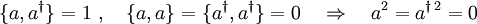

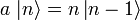
![[N,a]=[a^{\dagger}a,a]=\underbrace{[a^{\dagger},a]}_{2a^{\dagger}a-\{a,a^{\dagger}\}}a+a^{\dagger}\underbrace{[a,a]}_{0}=2a^{\dagger}\underbrace{aa}_{0}-\underbrace{\{a,a^{\dagger}\}}_{1}a=-a](/pictures/dewiki/101/ee52e3c5388c89e5f6ca1a110c1bde05.png)
![[N,a^{\dagger}]=[a^{\dagger}a,a^{\dagger}]=\underbrace{[a^{\dagger},a^{\dagger}]}_{0}a+a^{\dagger}\underbrace{[a,a^{\dagger}]}_{\{a,a^{\dagger}\}-2a^{\dagger}a}=a^{\dagger}\underbrace{\{a,a^{\dagger}\}}_{1}-2\underbrace{a^{\dagger}a^{\dagger}}_{0}a=a^{\dagger}](/pictures/dewiki/53/535bf1fc884ab26202acf17038ec8011.png)
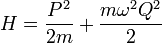

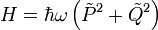
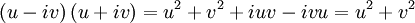
![\begin{array}{rcl}
H & = & \hbar\omega\left(\tilde{Q}^{2}+\tilde{P}^{2}\right)\\
& = & \hbar\omega\left(\tilde{Q}^{2}+\tilde{P}^{2}+i\left[\tilde{Q},\tilde{P}\right]-i\left[\tilde{Q},\tilde{P}\right]\right)\\
& = & \hbar\omega\left(\tilde{Q}^{2}+\tilde{P}^{2}+i\tilde{Q}\tilde{P}-i\tilde{P}\tilde{Q}-i\left[\tilde{Q},\tilde{P}\right]\right)\\
& = & \hbar\omega\left((\tilde{Q}-i\tilde{P})(\tilde{Q}+i\tilde{P})-i\left[\tilde{Q},\tilde{P}\right]\right)\end{array}](/pictures/dewiki/98/b78a06ecc8c2d0685a897278340cb255.png)
![\left[\tilde{Q},\tilde{P}\right]=\sqrt{\frac{m\omega}{2\hbar}}\frac{1}{\sqrt{2\hbar m\omega}}\underbrace{\left[Q,P\right]}_{i\hbar}=\frac{i}{2}](/pictures/dewiki/98/b0cc1047b53bba2085a35183bb0953ec.png)
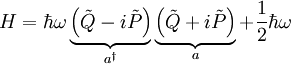
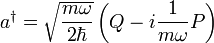
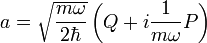
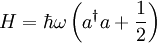
![\left[ a,a^{\dagger } \right]=aa^{\dagger }-a^{\dagger }a=\left( \tilde{Q}+i\tilde{P} \right)\left( \tilde{Q}-i\tilde{P} \right)-\left( \tilde{Q}-i\tilde{P} \right)\left( \tilde{Q}+i\tilde{P} \right)=2i\left( \tilde{P}\tilde{Q}-\tilde{Q}\tilde{P} \right)=2i\underbrace{\left[ \tilde{P},\tilde{Q} \right]}_{-i/2}=1](/pictures/dewiki/49/17e13bb92748ee0e5ff25d8b0d3db81d.png)