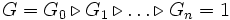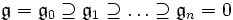- Auflösbar
-
In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen, surjektiv), kann aber auch ein Substantiv involvieren (z. B. vom Grad 3). Dieses Glossar soll insbesondere in Fällen, in denen ein und dasselbe Attribut auf Objekte ganz verschiedenen Typs (vgl. dazu: Hierarchie mathematischer Strukturen) angewandt wird, zur schnellen Orientierung dienen, Querverbindungen aufzeigen und vor möglichen Verwechslungen bewahren.
A
abelsch
- Eine Gruppe heißt abelsch (nach Niels Henrik Abel), wenn die Gruppenverknüpfung kommutativ ist.
- Eine Körpererweiterung heißt abelsche Erweiterung, wenn sie eine Galoiserweiterung mit abelscher Galoisgruppe ist.
- Eine Projektion e einer von-Neumann-Algebra A heißt abelsch, wenn eAe kommutativ ist.
abgeschlossen
- In der abstrakten Algebra heißt eine Menge abgeschlossen bezüglich einer auf ihren Elementen definierten Operation (z. B. einer zweistelligen Verknüpfung), wenn das Ergebnis der Operation, angewandt auf beliebige Elemente der Menge, wieder ein Element dieser Menge ist.
- Eine Teilmenge eines topologischen Raums heißt abgeschlossen, wenn ihr Komplement eine offene Menge ist.
- Siehe auch das Stichwort algebraisch abgeschlossen.
- In der Funktionalanalysis heißt ein Operator abgeschlossen, wenn sein Graph abgeschlossen ist.
abundant
Eine natürliche Zahl x heißt abundant, wenn ihre echte Teilersumme (die Summe aller Teiler ohne die Zahl selbst) größer ist als die Zahl x selbst. Vergleiche die Attribute defizient und vollkommen in diesem Glossar.
abzählbar
- Eine Menge bezeichnet man als abzählbar (oder abzählbar unendlich), wenn sie mit der Menge der natürlichen Zahlen gleichmächtig ist. Je nach Definition können auch endliche Mengen abzählbar heißen. Mächtigere Mengen heißen überabzählbar.
adaptiert
- Ein stochastischer Prozess
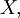 der auf einem Wahrscheinlichkeitsraum
der auf einem Wahrscheinlichkeitsraum 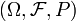 mit zugehöriger Filtrierung
mit zugehöriger Filtrierung 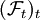 definiert ist, heißt adaptiert, wenn die Zufallsvariable
definiert ist, heißt adaptiert, wenn die Zufallsvariable 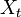 für jedes
für jedes 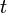
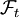 -messbar ist.
-messbar ist.
adjungiert
- In der linearen Algebra heißt ein Endomorphismus g eines (euklidischen oder unitären, also mit einem Skalarprodukt < , > ausgestatteten) k-Vektorraums W adjungiert zu einem Endomorphismus f eines (ebenfalls euklidischen oder unitären) k-Vektorraums V, falls für alle v in V und alle w in W gilt:
-
- <fv, w> = <v, gw>.
- Im Fall endlichdimensionaler Vektorräume entspricht dem adjungierten Endomorphismus die transponierte Matrix (im Fall einer Bilinearform) bzw. die konjugiert-transponierte Matrix (im Fall einer Sesquilinearform). Ist ein Endomorphismus gleich seinem adjungierten Endomorphismus, so heißt er selbstadjungiert oder symmetrisch (für Bilinearformen) bzw. hermitesch (für Sesquilinearformen).
- Siehe auch: Adjungierte Matrix, Adjungierter Operator
- In der Kategorientheorie heißen Paare (F: C → D, G: D → C) von Funktoren zwischen Kategorien C und D adjungiert, wenn für alle Objekte X von C und Y von D gilt:
-
- MorD(FX, Y) = MorC(X, GY).
- siehe auch: Adjunktion (Kategorientheorie)
- Nicht mit den ersten beiden genannten Begriffen verwandt ist die Adjunktion von Unbestimmten zu einem Körper oder Ring, siehe Adjunktion (Algebra)
- In der Theorie der Liegruppen bzw. algebraischen Gruppen nennt man die Konjugationsdarstellung der Gruppe auf ihrer Liealgebra, die im Fall von Matrizengruppen durch
-
- gegeben ist, die adjungierte Darstellung.
- In der Theorie der Liealgebren ist die adjungierte Darstellung die Darstellung der Liealgebra auf sich selbst, die durch die Lieklammer gegeben ist:
affin
- Eine Funktion der Form f(x) = ax + b heißt affin-linear, siehe auch affine Abbildung.
- Ein affiner Raum ist ein „Vektorraum ohne Ursprung“, d. h. es gibt zu je zwei Punkten A,B einen Vektor
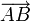 , so dass die Verschiebung um diesen Vektor A auf B abbildet. Die Menge dieser Verschiebungen bildet einen Vektorraum, aber im affinen Raum selbst gibt es keinen ausgezeichneten Punkt wie den Ursprung eines Vektorraums. Beispielsweise sind Geraden und Ebenen im Anschauungsraum affine Räume.
, so dass die Verschiebung um diesen Vektor A auf B abbildet. Die Menge dieser Verschiebungen bildet einen Vektorraum, aber im affinen Raum selbst gibt es keinen ausgezeichneten Punkt wie den Ursprung eines Vektorraums. Beispielsweise sind Geraden und Ebenen im Anschauungsraum affine Räume. - S. auch affine Ebene.
- Ein Koordinatensystem ist affin, wenn die Koordinatenachsen durch Geraden gebildet werden, siehe Affine Koordinaten
- Ein affines Schema ist ein Schema, das isomorph zum Spektrum eines Ringes ist. Ein Spezialfall ist:
- Eine affine algebraische Varietät ist eine algebraische Varietät, die sich als abgeschlossene Menge in einen affinen Raum einbetten lässt.
- Eine Inzidenzstruktur oder ein Blockplan heißen affin, wenn sie über einen Parallelismus verfügen, bei dem sich je zwei Blöcke in einer konstanten Zahl von Punkten schneiden.
ähnlich
- In der Geometrie sind zwei Figuren ähnlich, wenn sie durch Verschiebung, Drehung, Spiegelung und isotrope Streckung (oder Dilatation) ineinander überführt werden können. Ähnlichkeit erweitert also Kongruenz (Geometrie) um die Möglichkeit der Streckung.
- In der linearen Algebra heißen zwei quadratische Matrizen A und B ähnlich, wenn sie dieselbe lineare Abbildung bei Verwendung unterschiedlicher Basen beschreiben. Sie lassen sich durch eine invertierbare Matrix S ineinander überführen, A = S B S−1. Ähnlichkeit ist hier ein Spezialfall von Äquivalenz.
- Ordnungstreue bjiektive Abbildungen heißen ähnlich.
algebraisch
- Eine algebraische Gleichung entsteht durch Nullsetzen einer ganzrationalen Funktion (oder „Polynomfunktion“) f. Ihre Lösungen sind die Nullstellen von f.
- Eine Funktion heißt algebraisch, wenn alle Paare aus Punkt und Funktionswert Lösungen derselben algebraischen Gleichung sind. Andernfalls heißt die Funktion transzendent.
- In der Funktionentheorie heißt eine hebbare Singularität auch algebraisch.
- Eine komplexe Zahl heißt algebraisch, wenn sie Nullstelle eines Polynoms mit rationalen Koeffizienten ist. Die Menge (genauer: Der Körper) der algebraischen Zahlen bildet den algebraischen Abschluss der Menge
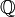 (der rationalen Zahlen).
(der rationalen Zahlen). - Ein Element einer Körpererweiterung heißt algebraisch, wenn es Nullstelle eines Polynoms mit Koeffizienten aus dem zu erweiternden Körper ist, siehe algebraisches Element.
algebraisch abgeschlossen
- Ein Körper K heißt algebraisch abgeschlossen, wenn jedes Polynom vom Grad ≥ 1 mit Koeffizienten aus K eine Nullstelle in K hat. Dann zerfällt in K jedes Polynom in lineare Faktoren (vom Grad 1). Der Körper der komplexen Zahlen ist algebraisch abgeschlossen, der der reellen Zahlen nicht. Siehe auch algebraischer Abschluss.
alternierend
Die Grundbedeutung von alternierend ist „abwechselnd“. In vielen Fällen sind damit abwechselnde Vorzeichen gemeint.
- Die alternierende Quersumme einer natürlichen Zahl in Dezimaldarstellung erhält man, indem man, von rechts nach links, die Ziffern abwechselnd subtrahiert und addiert.
- Die alternierende harmonische Folge ist die Folge der Zahlen
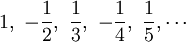
- Eine alternierende Reihe ist eine Reihe, bei der die Reihenglieder abwechselnd positiv und negativ sind. Ein einfaches Beispiel einer alternierenden Reihe ist die aus der alternierenden harmonischen Folge gebildete (alternierende harmonische) Reihe.
- Eine alternierende Multilinearform ist eine Multilinearform, die ihr Vorzeichen wechselt, wenn man zwei beliebige Argumente vertauscht.
- Die alternierende Gruppe An ist die Gruppe der geraden Permutationen einer n-elementigen Menge.
- In der Graphentheorie ist ein alternierender Pfad (bezüglich einer Paarung) ein Pfad, dessen Kanten abwechselnd zur Paarung und nicht zur Paarung gehören.
analytisch
- In der Theorie analytischer Funktionen heißt eine Menge analytisch, wenn sie als Nullstellengebilde von analytischen Funktionen darstellbar ist.
- In der Deskriptiven Mengenlehre heißt eine Teilmenge eines Polnischen Raums (z. B.
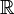 oder
oder 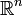 ) analytisch, wenn sie das Bild einer Borel-Menge unter einer stetigen Abbildung ist.
) analytisch, wenn sie das Bild einer Borel-Menge unter einer stetigen Abbildung ist. - In der Funktionentheorie heißt eine Funktion einer oder mehrerer komplexer Veränderlicher analytisch, wenn sie lokal durch eine konvergente Potenzreihe gegeben ist. Das ist (im Gegensatz zur reellen Analysis) äquivalent dazu, dass die Funktion beliebig oft komplex differenzierbar ist, und das wiederum ist (erneut im Gegensatz zur reellen Analysis) äquivalent dazu, dass die Funktion stetig und differenzierbar, also holomorph oder regulär ist. Tatsächlich werden in der Funktionentheorie, das heißt in der komplexen Analysis, die Begriffe analytisch, holomorph und regulär äquivalent gebraucht.
- Auch in der reellen Analysis heißt eine Funktion analytisch wenn sie lokal durch eine Potenzreihe gegeben ist.
- Die Lösung eines Problems wird als analytisch bezeichnet, wenn sie – im Gegensatz zu numerischen Lösungen – in Form von bekannten Funktionen, Konstanten etc. angeschrieben werden kann.
antisymmetrisch
- Eine Relation R heißt antisymmetrisch, wenn aus xRy und yRx folgt, dass x und y gleich sind. Dies ist eine der definierenden Eigenschaften einer partiellen Ordnung.
- Eine multilineare Abbildung heißt antisymmetrisch, wenn ihr Wert beim Vertauschen zweier ihrer Argumente das Vorzeichen wechselt.
äquidistant
bedeutet gleich weit entfernt.
äquivalent
- Zwei Aussagen heißen äquivalent, wenn sie unter gleichen Voraussetzungen denselben Wahrheitswert haben. Insbesondere heißen zwei Gleichungen mit einer oder mehreren Unbekannten äquivalent, wenn sie dieselbe Lösungsmenge haben.
- Zwei Elemente einer Menge heißen äquivalent, wenn sie in der gleichen Äquivalenzklasse bezüglich einer Äquivalenzrelation liegen.
- In der linearen Algebra heißen zwei m×n Matrizen A und B äquivalent, wenn es invertierbare Matrizen S und T gibt, sodass A = S·B·T. Äquivalente Matrizen beschreiben bezüglich geeigneter Basen die gleiche lineare Abbildung; Matrizen sind genau dann äquivalent, wenn sie den gleichen Rang haben. Falls die äquivalenten Matrizen A und B quadratisch sind (m=n) und T=S−1 gewählt werden kann, sind A und B sogar ähnlich.
- Zwei Darstellungen heißen äquivalent, wenn sie bis auf Basenwechsel aus den gleichen linearen Abbildungen bestehen.
assoziativ
- Eine zweistellige Verknüpfung * heißt assoziativ, wenn für alle Elemente a, b und c der Grundmenge stets die Gleichung a*(b*c) = (a*b)*c gilt. Die Assoziativität der Verknüpfung erlaubt, die Klammern wegzulassen und einfach a*b*c zu schreiben.
Eine Menge A und eine zweistellige Verknüpfung * auf A, deren Ergebnisse alle in A liegen, wird als Magma bezeichnet. Ist diese Verknüpfung darüber hinaus auch assoziativ spricht man von einer Halbgruppe.
asymmetrisch
- Eine Relation R heißt asymmetrisch, wenn aus xRy stets nicht yRx folgt. Insbesondere gilt nicht xRx. Dies ist eine der Eigenschaften einer strikten partiellen Ordnung.
auflösbar
-
- von Normalteilern gibt, deren Quotienten (auch „Faktorgruppen“) Gk/Gk+1 abelsch sind.
- Eine Liealgebra heißt auflösbar, wenn es eine absteigende Folge
-
- von Idealen gibt (d. h.
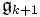 soll ein Ideal in
soll ein Ideal in 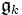 sein), deren Quotienten abelsch sind.
sein), deren Quotienten abelsch sind.
ausgeartet
- Eine bilineare Abbildung b (eine Bilinearform) heißt ausgeartet, wenn es einen Vektor x ≠ 0 gibt, der für jeden Vektor y die Gleichung b(x, y) = 0 erfüllt. Für das Gegenteil gibt es die Begriffe regulär oder perfekt, meist sagt man aber schlicht „nicht ausgeartet“.
B
befreundet
- Ein Paar natürlicher Zahlen heißt befreundet, wenn die Summe der echten Teiler der einen Zahl die jeweils andere ergibt. Beispiel: 220 und 284 (1+2+4+5+10+11+20+22+44+55+110 = 284, 1+2+4+71+142 = 220). Siehe befreundete Zahl.
beschränkt
- Eine Teilmenge U eines metrischen Raums (X,d) heißt beschränkt, wenn es eine positive reelle Zahl c gibt, sodass der Abstand zweier Elemente von U stets kleiner oder gleich c ist, wenn also die Abstände in U beschränkt sind.
- Als Spezialfall davon heißt eine Menge U reeller Zahlen beschränkt, wenn es zwei reelle Zahlen a und b gibt, sodass U eine Teilmenge des abgeschlossenen Intervalls [a,b] ist.
- Eine Funktion heißt beschränkt, wenn ihr Bildbereich eine beschränkte Menge ist.
- Ein linearer Operator zwischen normierten Räumen heißt beschränkter Operator, wenn er stetig ist.
- Eine stark stetige Halbgruppe heißt beschränkt, wenn die Menge der zugehörigen Operatoren eine norm-beschränkte Menge ist.
bijektiv
- Eine Funktion heißt bijektiv oder umkehrbar eindeutig (engl.: bijective oder one-to-one and onto), wenn sie injektiv und surjektiv ist, also verschiedenen Elementen der Definitionsmenge verschiedene Elemente der Wertemenge zuordnet, wobei jedes Element der Wertemenge erreicht wird. Bijektive Funktionen sind invertierbar. Ein bijektiver Homomorphismus heißt Isomorphismus.
bilinear
- Eine Funktion f: V×W → X zu gegebenen Vektorräumen heißt bilinear, wenn sie bei festgehaltenem ersten Argument linear im zweiten Argument und bei festgehaltenem zweiten linear im ersten Argument ist. Wenn W=V ist und X der dem Vektorraum unterliegende Körper, heißt f Bilinearform. Über dem Körper der komplexen Zahlen betrachtet man oft sesquilineare statt bilinearer Funktionen.
bivariat
- Eine Funktion ist bivariat, wenn sie genau zwei unbestimmte Variablen enthält (z. B. 3x2y + y2x − x2y3).
- Die gemeinsame Verteilung zweier Zufallsvariablen ist bivariat (s. Hauptartikel: Bivariate Verteilung).
C
chaotisch
Als mathematischer Begriff (s. Chaostheorie) Ausdruck eines schlecht gestellten (engl. „ill posed“) inversen Problems. Mittels einfacher, meist sogar deterministischer Regeln kann ein komplexes Objekt erzeugt werden, jedoch ist der Rückschluss vom Objekt auf die erzeugenden Regeln nicht oder nur schlecht möglich.
charakteristisch
- In der Mengenlehre hat die charakteristische Funktion einer Teilmenge, auch Indikatorfunktion genannt, den Wert 1 auf der Teilmenge und 0 außerhalb.
- Charakteristisches Polynom und charakteristische Gleichung einer Matrix oder eines Operators, siehe Eigenvektor.
- In der Gruppentheorie ist eine charakteristische Untergruppe einer Gruppe G eine Untergruppe H, die unter jedem Automorphismus von G fest bleibt. Das heißt, eine Untergruppe H von G heißt charakteristisch, wenn für jeden Automorphismus (d. h. bijektiven Gruppenhomomorphismus von G nach G) f gilt, dass f(H) gleich H ist.
D
definit
- Siehe positiv definit und negativ definit.
defizient
Eine natürliche Zahl heißt defizient, wenn ihre echte Teilersumme (die Summe aller Teiler ohne die Zahl selbst) kleiner ist als die Zahl selbst. Vergleiche auch die Attribute abundant und vollkommen in diesem Glossar.
diagonaldominant
Eine Matrix heißt diagonaldominant, falls das Zeilensummenkriterium erfüllt ist, d. h. falls der Betrag jedes Diagonalelementes größer ist als die Summe der Beträge der restlichen jeweiligen Zeilenelemente.
diagonalisierbar
- Eine Matrix A heißt diagonalisierbar, wenn es eine invertierbare Matrix S gibt, sodass
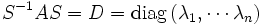 eine Diagonalmatrix ist (Die Matrizen A und D sind ähnlich). Dies ist beispielsweise dann der Fall, wenn das Charakteristische Polynom in Linearfaktoren zerfällt und die algebraischen gleich den geometrischen Vielfachheiten der Eigenwerte sind.
eine Diagonalmatrix ist (Die Matrizen A und D sind ähnlich). Dies ist beispielsweise dann der Fall, wenn das Charakteristische Polynom in Linearfaktoren zerfällt und die algebraischen gleich den geometrischen Vielfachheiten der Eigenwerte sind.
dicht
- Eine Teilmenge M liegt dicht in einem topologischen Raum R, wenn es keine abgeschlossene Teilmenge von R außer R selbst gibt, die M enthält. Mit anderen Worten, M ist dicht (in R), wenn der Abschluss von M mit R übereinstimmt. Beispiel: die Menge der rationalen Zahlen Q liegt dicht in der Menge der reellen Zahlen R (und macht diese dadurch separabel).
- Die Teilordnung S einer geordneten Menge M heißt dicht, wenn es zu jedem x und y aus M mit x < y ein z aus S gibt, sodass x < z < y ist. Beispiel: die übliche Ordnung der rationalen oder der reellen Zahlen ist dicht. Siehe Ordnungstopologie.
differenzierbar
- Die Funktion f heißt differenzierbar an der Stelle x0, falls der Limes des Differenzenquotienten an der Stelle x0 existiert.
Dimension
- In der linearen Algebra ist die Dimension eines Vektorraums die Anzahl seiner Basisvektoren, also die minimale Ordnung eines Erzeugendensystems. Diese Dimension heißt, falls unendlich, auch Hamel-Dimension.
- Die Dimension einer Mannigfaltigkeit ist die Anzahl der Koordinaten in einem lokalen Koordinatensystem. Dass eine Mannigfaltigkeit eine eindeutige Dimension hat, ist gesichert, wenn sie zusammenhängt.
- Die Hausdorff-Dimension kann nichtganzzahlig sein und wird zur Beschreibung von Fraktalen verwandt.
disjunkt
- Zwei Mengen heißen disjunkt, wenn sie kein gemeinsames Element besitzen.
diskret
- Eine Teilmenge M der reellen Zahlen heißt diskret, wenn es zu jedem Element
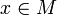 ein offenes Intervall gibt, das x enthält, aber außer x kein weiteres Element von M.
ein offenes Intervall gibt, das x enthält, aber außer x kein weiteres Element von M. - Eine von-Neumann-Algebra vom Typ I wird diskret genannt.
- Eine Zufallsvariable
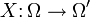 heißt diskret, wenn sie nur endlich viele oder abzählbar unendlich viele Werte annimmt.
heißt diskret, wenn sie nur endlich viele oder abzählbar unendlich viele Werte annimmt.
dual
- Sei V ein Vektorraum über einem Körper K. Dann heißt der Vektorraum V*:=HomK(V,K), der die linearen Abbildungen von V nach K enthält, dual zu V (Dualraum).
- In einer Booleschen Algebra entsteht eine duale Aussage, wenn man alle Elementaraussagen negiert, 0 mit 1 und ∧ mit ∨ vertauscht, und die gesamte Aussage negiert.
- Analog dazu geht ein komplementärer Verband (z. B. eine Mengenalgebra) in sein duales Gegenstück über, wenn man die beiden inneren Verknüpfungen miteinander vertauscht und jedes Element durch sein Komplement ersetzt.
- Zu einer lokalkompakten abelschen Gruppe betrachtet man die Dualgruppe.
- Eine duale C*-Algebra ist eine C*-Algebra kompakter Operatoren.
E
echt
- Eine Teilmenge heißt echt, wenn sie nicht identisch ist mit der Grundmenge.
- Ein Teiler bzw. Faktor einer natürlichen Zahl heißt echt, wenn er kleiner als die Zahl selbst ist. Die Menge der echten Teiler einer Zahl ist somit die Menge der Teiler ohne die Zahl selbst.
- Projektionen und von-Neumann-Algebren können die Eigenschaft echt unendlich haben, wie in der Typklassifikation von von-Neumann-Algebren erläutert.
eigentlich
- Eine Abbildung zwischen topologischen Räumen heißt eigentlich, wenn unter ihr alle Urbilder kompakter Mengen wieder kompakt sind.
eindeutig
- In älterer Literatur heißt eine injektive Abbildung eindeutig.
- das Gegenteil von mehrdeutig.
- Nach moderner Auffassung sind Abbildungen („Funktionen“) nach Definition eindeutig. Was früher „mehrdeutige Funktion“ genannt wurde, ist heutzutage eine Relation, aber keine Funktion.
eineindeutig
- Von der Verwendung dieses veralteten Attributs ist abzuraten, da es uneinheitlich verwendet wurde: überwiegend in der Bedeutung bijektiv, zuweilen aber auch in der Bedeutung injektiv.
einfach
- Eine Gruppe heißt einfach, wenn sie mindestens zwei Elemente und keinen nichttrivialen Normalteiler besitzt. Die Menge {e}, die nur das Einselement enthält, und die Gruppe selbst werden als triviale Normalteiler angesehen. Siehe auch Einfache Gruppe.
- Ein Modul heißt einfach, wenn er keine echten Untermoduln hat.
- Ein Ring heißt einfach, wenn er keine nichttrivialen zweiseitigen Ideale besitzt. Ist R nicht-kommutativ, so ist die Einfachheit von R als links-R-Modul restriktiver als die ringtheoretische Einfachheit.
- Eine Inzidenzstruktur oder ein Blockplan heißen einfach, wenn man ihre Blöcke als Punktmengen und ihre Inzidenzrelation als mengentheoretisches Enthaltensein auffassen kann.
- Eine einfache Funktion ist eine messbare Funktion mit einer abzählbaren Menge von Funktionswerten.
einfach zusammenhängend
- Ein topologischer Raum heißt einfach zusammenhängend, wenn in ihm jede geschlossene Kurve zu einem Punkt zusammengezogen werden kann, d. h. wenn die Fundamentalgruppe trivial ist.
- Äquivalent dazu: Eine offene Menge D heißt (homotop) einfach zusammenhängend, falls jede geschlossene Kurve in D nullhomotop ist.
elliptisch
- In der Geometrie eine Kurve zweiter Ordnung, die Ellipse heißt.
- In der Analysis sind die elliptischen Funktionen eine wichtige Klasse spezieller Funktionen; die einfachsten unter ihnen treten als Umkehrfunktionen elliptischer Integrale auf.
- Eine fundamentale Klasse partieller Differentialgleichungen heißt elliptisch.
- Eine fundamentale Klasse nichteuklidischer Geometrien heißt elliptisch. Sie ist dadurch ausgezeichnet, dass in ihr die Winkelsumme jedes Dreiecks größer als 180 Grad ist.
- Eine elliptische Kurve ist eine singularitätenfreie algebraische Kurve vom Grad 3 in der projektiven Ebene mit einem ausgezeichneten rationalen Punkt. Von besonderem Interesse z. B. für die Faktorisierung natürlicher Zahlen sind aufgrund ihrer einfachen Struktur elliptische Kurven der Form cy2 = x3 + ax + b mit c ≠ 0 und 4a3 + 27b2 ≠ 0.
endlich
- Eine Menge heißt endlich, wenn ihre Mächtigkeit (die Anzahl ihrer Elemente) eine natürliche Zahl ist. Oder äquivalent: wenn keine Bijektion zwischen der Menge und einer ihrer echten Teilmengen existiert.
- Ein Maß heißt endlich, wenn das Maß der Grundmenge Ω des Maßraums eine endliche Zahl ist. Ein Maß heißt σ-endlich, wenn Ω die abzählbare Vereinigung messbarer Mengen endlichen Maßes ist.
- In der Gruppentheorie ist die Unterscheidung zwischen endlichen und unendlichen Gruppen fundamental.
- Projektionen und von-Neumann-Algebren können endlich sein, wie in der Typklassifikation von von-Neumann-Algebren erläutert.
- In der Physik verwendet man das Wort endlich auch, um „von Null verschieden“ zu sagen.
entartet
- Ein einfacher Grenzfall eines eigentlich andersartigen mathematischen Objektes heißt entartet. So ist etwa ein Punkt ein entarteter Kreis (mit Radius 0).
- Eine bilineare Abbildung b (eine Bilinearform) heißt entartet oder ausgeartet, wenn es einen Vektor x ≠ 0 gibt, der für jeden Vektor y die Gleichung b(x, y) = 0 erfüllt. Das Gegenteil wird manchmal mit dem Wort regulär bezeichnet, meist spricht man aber einfach von „nicht entartet“ bzw. „nicht ausgeartet“.
- Ein Eigenwert heißt l-fach entartet, wenn der zugehörige Eigenraum Dimension l > 1 hat.
erwartungstreu
- Eine Schätzfunktion g(θ) heißt erwartungstreu, wenn ihr Erwartungswert unter einer parametrischen Verteilung Pθ für alle θ mit dem zu schätzenden Funktional γ(θ) übereinstimmt.
euklidisch
- Ein euklidischer Raum ist ein reeller affiner Raum mit dem üblichen Skalarprodukt. In einem solchen Raum gelten die Axiome der euklidischen Geometrie. In manchen Kontexten wird nur der dreidimensionale Raum als euklidisch bezeichnet.
- Ein euklidischer Ring ist ein Ring, in dem eine (verallgemeinerte) Division mit Rest vorhanden ist, wie man sie von den ganzen Zahlen kennt.
- Eine Relation R heißt euklidisch, wenn aus xRy und xRz auch yRz folgt.
exakt
- Exakte Differentialgleichungen sind gewöhnliche Differentialgleichungen eines bestimmten Typs.
- Exakte Funktoren werden in der Kategorientheorie untersucht.
- Eine exakte Sequenz ist eine Sequenz, bei der an jeder Stelle Kern und Bild übereinstiimen.
F
faktoriell
- Ein Integritätsring heißt faktoriell, wenn jede von Null verschiedene Nichteinheit eine (bis auf Assoziiertheit und Reihenfolge) eindeutige Zerlegung in irreduzible Elemente besitzt.
fast abgeschlossen
- Eine Menge M heißt bezüglich der Relation R fast R-abgeschlossen, wenn
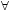 x
x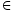 M(
M(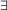 y(xRy)
y(xRy) 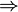
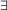 z
z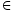 M (xRz)).
M (xRz)).
fast alle
- Man sagt, dass eine Eigenschaft E für fast alle Elemente einer Menge oder Folge gilt, wenn sie für alle bis auf endlich viele gilt. Zum Beispiel gilt für eine konvergente Folge, dass in jeder Umgebung des Grenzwertes fast alle Folgenglieder enthalten sind.
fast überall
- Man sagt, dass eine Eigenschaft E fast überall in einer Menge X gilt, wenn auf X ein Maß definiert ist und die Menge der Punkte, für die die Eigenschaft E nicht gilt, eine Nullmenge ist. Wenn die Menge X Teilmenge eines Euklidischen Raums ist, die Punkte von X also reelle Koordinaten haben, legt man in der Regel das Lebesgue-Maß zugrunde. Siehe Nullmenge für weitere Erklärungen und Beispiele.
fast sicher
- Man sagt, dass ein Ereignis auf einem Wahrscheinlichkeitsraum fast sicher (f. s. oder engl. a. e. für „almost everywhere“) eintritt, wenn dessen Wahrscheinlichkeit 1 beträgt. D. h. das Ereignis tritt fast überall auf dem Wahrscheinlichkeitsraum, als Maßraum betrachtet, ein. Die Definition ist äquivalent zu der Definition von fast überall aus der Maßtheorie.
fein, feiner, feinst
Diese Attribute dienen in der Topologie dem Vergleich verschiedener topologischer Strukturen auf derselben Menge. Siehe Topologischer Raum.
fett
Als fette Menge wird eine Teilmenge eines topologischen Raums X bezeichnet, die nicht mager ist, s. Satz von Baire.
fraktal
In der Mathematik Bezeichnung für Mengen mit gebrochener Hausdorff-Dimension, selbstähnliche Mengen (s. auch IFS-Fraktal) oder selbstähnliche Funktionen; siehe auch Fraktale Dimension.
frei
- Aus nichtleeren Mengen kann man durch geeignete Konstruktionen algebraische Strukturen gewinnen, die gerade nur soviele Eigenschaften haben, wie von den Axiomen der Strukturen gefordert wird. Beispiele sind freies Gruppoid, freie Halbgruppe, freies Monoid, freie Gruppe, freie abelsche Gruppe.
- Ein Modul heißt frei, wenn er eine Basis hat. Eine Basis ist hier ein linear unabhängiges Erzeugendensystem.
G
ganz
- Eine in ganz
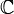 holomorphe Funktion heißt ganze Funktion.
holomorphe Funktion heißt ganze Funktion. - In der Algebra heißt ein Element einer Ringerweiterung B / A ganz, wenn es Nullstelle eines normierten Polynomes mit Koeffizienten aus A ist.
- Als Spezialfall hiervon heißt ein Element einer Körpererweiterung K von
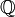 (algebraisch) ganz oder ganzalgebraisch, wenn es Nullstelle eines normierten Polynoms mit Koeffizienten aus
(algebraisch) ganz oder ganzalgebraisch, wenn es Nullstelle eines normierten Polynoms mit Koeffizienten aus 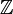 ist.
ist. - Eine Ringerweiterung heißt ganz, wenn alle Elemente ganz sind.
gerade
- Eine Funktion f(x) heißt gerade, wenn f(x) = f(−x) für alle x aus der Grundmenge gilt. Der Graph einer geraden Funktion ist achsensymmetrisch zur y-Achse.
- Eine ganze Zahl heißt gerade, wenn sie durch 2 teilbar ist. Siehe Parität
- Eine Permutation σ heißt gerade, wenn sie eine gerade Anzahl von Fehlständen hervorbringt. Ein Fehlstand ist ein Paar i, j mit i<j aber σ(i)>σ(j). Siehe alternierende Gruppe.
geordnet
glatt
- Bei Funktionen, Kurven, Mannigfaltigkeiten und anderen differenzierbaren Objekten: Oft salopp gebraucht in der Bedeutung „genügend oft differenzierbar“. Manchmal formal definiert als „beliebig oft differenzierbar“. Im Falle von Kurven im
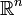 steht glatt oft auch lediglich für stetig differenzierbar – siehe auch glatte Kurve und glatte Funktion.
steht glatt oft auch lediglich für stetig differenzierbar – siehe auch glatte Kurve und glatte Funktion.
gleichmäßig beschränkt
Sei
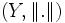 ein normierter Raum. Eine Klasse von Funktionen F von
ein normierter Raum. Eine Klasse von Funktionen F von 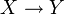 heißt gleichmäßig beschränkt, wenn es eine Konstante
heißt gleichmäßig beschränkt, wenn es eine Konstante 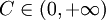 gibt mit
gibt mit 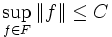 .
.gleichmäßig konvergent
- Sei
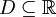 . Eine Funktionenfolge
. Eine Funktionenfolge 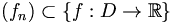 heißt gleichmäßig konvergent, wenn gilt:
heißt gleichmäßig konvergent, wenn gilt: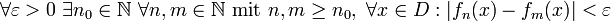
gleichmäßig stetig
- Seien (X,d1) und (Y,d2) metrische Räume. Eine Funktion f von
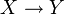 heißt gleichmäßig stetig genau dann, wenn zu jedem
heißt gleichmäßig stetig genau dann, wenn zu jedem 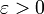 ein δ > 0 existiert mit
ein δ > 0 existiert mit 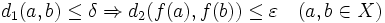 .
.
gleichgradig stetig
- Seien (X,d1) und (Y,d2) metrische Räume. Eine Menge F von Funktionen
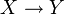 heißt gleichgradig stetig im Punkt x0 wenn zu jedem
heißt gleichgradig stetig im Punkt x0 wenn zu jedem 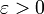 ein δ > 0 existiert mit
ein δ > 0 existiert mit 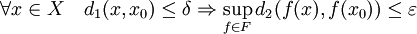 . Die Menge F heißt gleichgradig stetig, wenn sie in jedem Punkt gleichgradig stetig ist.
. Die Menge F heißt gleichgradig stetig, wenn sie in jedem Punkt gleichgradig stetig ist.
- Die Menge F heißt gleichgradig gleichmäßig stetig, wenn δ unabhängig von x0 gewählt werden kann, also falls gilt:
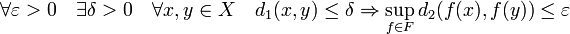 .
.- Spezialfall: Sei
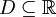 . Eine Menge von Funktionen
. Eine Menge von Funktionen 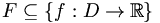 heißt gleichgradig stetig genau dann, wenn
heißt gleichgradig stetig genau dann, wenn 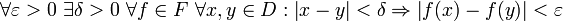
global
- Nicht auf eine Umgebung bezogen, also nicht lokal, sondern auf eine gesamte Grundmenge.
Grad
- In der Geometrie ist das Grad Maßeinheit für die Größe eines ebenen Winkels.
- In der Algebra ist der Grad eines Summanden in einem Polynom der Exponent, mit dem die Variable in diesem Term potenziert ist; der Grad des Polynoms ist der größte Grad eines in dem Polynom enthaltenen Summanden.
- In der Darstellungstheorie ist der Grad der Darstellung die Dimension des Vektorraums, in dem die Darstellung stattfindet.
- In der Graphentheorie ist der Grad einer Ecke die Anzahl der in dieser Ecke zusammentreffenden Kanten.
- Für den Grad einer Karte zwischen Mannigfaltigkeiten, siehe [1].
grob, gröber, gröbst
Diese Attribute dienen in der Topologie dem Vergleich verschiedener topologischer Strukturen auf derselben Menge. Siehe Topologischer Raum.
größtes Element
- Ein Element x einer halbgeordneten Menge heißt größtes Element, wenn alle anderen Elemente kleiner sind, d. h. für jedes Element y die Relation x ≥ y gilt. Das größte Element einer halbgeordneten Menge existiert nicht immer, ist aber im Falle seiner Existenz eindeutig bestimmt. Siehe auch maximal und kleinstes Element.
H
harmonisch
- Harmonische Funktionen werden vom Laplace-Operator auf 0 abgebildet.
- Eine harmonische Schwingung ist eine Schwingung, die durch eine Sinusfunktion beschrieben werden kann.
- Die harmonische Reihe ist die divergente Reihe 1 + 1/2 +1/3 + 1/4 + ... aller Stammbrüche.
- Das harmonische Mittel ist eine spezielle Art der Mittelwertbildung.
- Die harmonische Teilung bezeichnet in der Geometrie ein besonderes Lageverhältnis von vier Punkten auf einer Geraden.
- Harmonische Analyse ist die Theorie der lokalkompakten abelschen Gruppen.
Hausdorffraum
- Ein topologischer Raum ist ein Hausdorff-Raum, wenn das Trennungsaxiom T2 gilt: jedes Paar von verschiedenen Punkten besitzt disjunkte Umgebungen.
hebbar
- In der Funktionentheorie heißt eine Singularität a einer analytischen Funktion f hebbar (auch algebraisch oder regulär), wenn eine analytische
Funktion
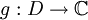 existiert mit g = f in
existiert mit g = f in 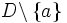 .
.- Eine Definitionslücke, in die eine Funktion stetig fortgesetzt werden kann, heißt stetig behebbare Definitionslücke.
hermitesch
- Das Adjektiv hermitesch (oder auch Hermitesch) leitet sich von Charles Hermite her, es gibt auch die (falsche) Schreibweise „hermitisch“.
- Die hermitesch adjungierte bzw. hermitesch konjungierte Matrix zu einer Matrix A ist die komplex Konjugierte der Transponierten (oder umgekehrt) von A,
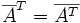 . Alle komplexen Matrizen und Vektoren lassen sich hermitesch konjugieren; die hermitesch Konjugierte einer reellen Matrix ist einfach die Transponierte. Gängige Schreibweisen für die hermitesch Konjungierte von A sind
. Alle komplexen Matrizen und Vektoren lassen sich hermitesch konjugieren; die hermitesch Konjugierte einer reellen Matrix ist einfach die Transponierte. Gängige Schreibweisen für die hermitesch Konjungierte von A sind 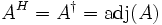 . Die Notation A * steht je nach Autor für die hermitesch adjungierte bzw. hermitesch konjungierte oder aber für die nur komplex konjugierte Matrix. Sie ist daher zu vermeiden.
. Die Notation A * steht je nach Autor für die hermitesch adjungierte bzw. hermitesch konjungierte oder aber für die nur komplex konjugierte Matrix. Sie ist daher zu vermeiden.
- Zwei Matrizen A, B heißen adjungiert oder hermitesch adjungiert oder hermitesch konjugiert zueinander, wenn sie durch komplexe Konjugation und Transposition auseinander hervorgehen, das heißt B = AH.
- Eine Matrix heißt hermitesch oder selbstadjungiert genau dann, wenn sie zu sich selbst hermitesch adjungiert bzw. adjungiert ist, das heißt A = AH. Aus hermitesch folgt quadratisch, normal und daraus diagonalisierbar.
- Eine hermitesche Form ist eine Sesquilinearform
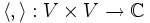 mit
mit 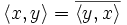 . Das innere Produkt in einem unitärem Raum ist per definitionem eine hermitesche Form.
. Das innere Produkt in einem unitärem Raum ist per definitionem eine hermitesche Form.
- In der Funktionalanalysis heißt ein linearer Operator f auf einem Hilbert-Raum selbstadjungiert, wenn er hermitesch ist und zusätzlich gewisse topologische Anforderungen erfüllt (so zumindest bei Dieudonné). In weniger formalen Darstellungen werden die Attribute hermitesch und selbstadjungiert austauschbar gebraucht. Bra-Ket-Notation:
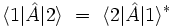 mit
mit 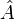 hermitesch.
hermitesch.
hinreichend
- Eine Aussage A ist eine hinreichende Bedingung einer anderen Aussage B, wenn zwischen den beiden Aussagen die logische Beziehung „aus A folgt B“ (kurz: A ⇒ B) besteht. Der Gegenbegriff ist notwendig. Siehe auch Notwendige und hinreichende Bedingung.
hölder-stetig
- Für metrische Räume (E,dE),(F,dF) heißt eine Funktion
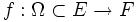 hölder-stetig mit Exponent
hölder-stetig mit Exponent 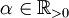 und Konstante
und Konstante 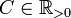 , falls für alle
, falls für alle 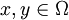 gilt
gilt 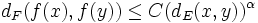
holomorph
- In der Funktionentheorie heißt eine Funktion einer komplexen Variablen holomorph oder regulär in einem Bereich, wenn sie in diesem Bereich eindeutig ist und eine stetige Ableitung hat; diese Definition impliziert Stetigkeit der Funktion selbst.
homogen
- Homogen ist ein Raum, der „überall gleich aussieht“:
- Ein topologischer Raum ist homogen, falls es für je zwei Punkte einen Homöomorphismus gibt, der den einen Punkt auf den anderen Punkt abbildet.
- Allgemeiner heißt eine Menge mit einer transitiven Gruppenaktion ein homogener Raum.
- Homogenität bezeichnet eine Art von Kompatibilität mit Skalarmultiplikation:
- Ein lineares Gleichungssystem heißt homogen, wenn seine m Gleichungen in den n Unbekannten die Form aj1x1 + … + ajnxn = 0 haben (für alle j aus 1, 2, …,m); Wenn auf der rechten Seite in mindestens einer Gleichung eine andere Zahl als die 0 steht, heißt das Gleichungssystem inhomogen.
Siehe: Homogene Gleichung - Eine Abbildung heißt homogen vom Grad p, falls für Skalare a die Gleichung f(ax) = apf(x) gilt; manchmal wird „homogen“ auch im Sinne von „homogen vom Grad 1“ benutzt.
Siehe: Homogene Abbildung, Homogenes Polynom - In Verallgemeinerung des Begriffs „homogenes Polynom“ heißen Elemente in einem graduierten Objekt (Ring, Algebra, Modul) homogen, wenn sie in einem der graduierten Bestandteile liegen. Ein graduierter Morphismus heißt homogen vom Grad p, wenn er den Grad um p erhöht.
Siehe: Graduierung (Algebra)
- Ein lineares Gleichungssystem heißt homogen, wenn seine m Gleichungen in den n Unbekannten die Form aj1x1 + … + ajnxn = 0 haben (für alle j aus 1, 2, …,m); Wenn auf der rechten Seite in mindestens einer Gleichung eine andere Zahl als die 0 steht, heißt das Gleichungssystem inhomogen.
- Eine Relation heißt homogen, wenn Vor- und Nachmenge übereinstimmen.
- In der Zahlentheorie heißen Zahlen homogen, wenn sie aus den gleichen Primfaktoren aufgebaut sind, wie beispielsweise
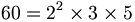 und
und 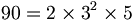 .
. - In der projektiven Geometrie werden homogene Koordinaten verwendet.
homöomorph
- Zwei topologische Räume X und Y heißen homöomorph, falls es eine bijektive Abbildung f : X -> Y gibt, sodass f und f -1 stetig sind. Vom Standpunkt der Topologie aus sind X und Y gleich. Die Funktion f wird Homöomorphismus genannt.
homotop
Zwei Teilmengen (oder zwei Kurven) eines topologischen Raums sind homotop, wenn sie sich stetig ineinander deformieren lassen.
hyperbolisch
- In der Geometrie eine Kurve zweiten Grades (auch „zweiter Ordnung“).
- Eine fundamentale Klasse partieller Differentialgleichungen heißt hyperbolisch.
- Eine fundamentale Klasse nichteuklidischer Geometrien heißt hyperbolisch. Darin ist die Winkelsumme im Dreieck immer kleiner als 180 Grad.
- Ein zweidimensionaler Bilinearraum (V, b) heißt hyperbolische Ebene, wenn er zwei Vektoren x und y mit der Eigenschaft b(x,x) = 0, b(y, y) = 0, b(x, y) = 1 enthält.
- Ein Bilinearraum, der als orthogonale Summe von hyperbolischen Ebenen dargestellt werden kann, heißt hyperbolischer Raum.
I
ideal
- In der Zahlentheorie wurden gewisse auf komplexe Wurzeln der Eins (Einheitswurzeln) aufgebaute Zahlen von Ernst Kummer ideal genannt; diese Idee wurde von Richard Dedekind zum abstrakt algebraischen Begriff Ideal verallgemeinert.
idempotent
- Eine Matrix A heißt idempotent, wenn AA = A gilt; allgemeiner:
- Ein Element e eines Monoiden heißt idempotent, wenn ee = e gilt.
indefinit
- Die Matrix A heißt indefinit, wenn A mindestens einen positiven und einen negativen Eigenwert besitzt.
inhomogen
- Für ein lineares Gleichungssystem siehe unter homogen.
injektiv
- Eine Funktion heißt injektiv, wenn niemals zwei verschiedene Elemente denselben Funktionswert haben. Eine injektive Funktion ist auf ihrer Wertemenge eindeutig umkehrbar und heißt deshalb auch eineindeutig. Ein injektiver Homomorphismus heißt auch Monomorphismus.
- Ein Objekt J einer Kategorie heißt injektiv, wenn sich Morphismen von Unterobjekten nach J stets auf das ganze Objekt ausdehnen lassen.
- Das injektive Tensorprodukt ist eine spezielle Variante des Tensorproduktes normierter oder lokalkonvexer Räume.
integrabel
- Eine Differentialgleichung nennt man integrabel, wenn es möglich ist, sie analytisch zu lösen, also eine Lösungsfunktion (das Integral) anzugeben. Sehr viele mathematische Probleme, insbesondere nichtlineare und partielle Differentialgleichungen sind nicht integrabel, darunter schon ganz einfach erscheinende wie die des Dreikörperproblems, des Doppelpendels oder der meisten Kreiseltypen.
invers
- Zwei mathematische Operationen heißen invers zueinander, wenn sich ihre Wirkung aufhebt. Beispiel: Integration ist invers zur Differentiation.
- Zwei Elemente einer Gruppe heißen invers zueinander, wenn ihre Verknüpfung das neutrale Element der Gruppe ergibt. Siehe Inverses Element.
invertierbar
- Eine Funktion
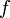 heißt invertierbar, wenn die Umkehrfunktion
heißt invertierbar, wenn die Umkehrfunktion 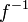 existiert. Dann gilt
existiert. Dann gilt 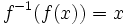 für alle
für alle 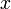 aus der Definitionsmenge von
aus der Definitionsmenge von 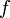 bzw.
bzw. 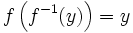 für alle
für alle 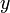 aus der Bildmenge von
aus der Bildmenge von 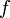 . Eine Funktion ist genau dann invertierbar, wenn sie bijektiv ist.
. Eine Funktion ist genau dann invertierbar, wenn sie bijektiv ist.
- In der linearen Algebra heißt eine quadratische Matrix A invertierbar, wenn die inverse Matrix A−1 existiert (s. Haupartikel: Reguläre Matrix).
involutorisch
- Eine quadratische Matrix heißt involutorisch, wenn ihr Quadrat die Einheitsmatrix ist.
- Eine Abbildung heißt involutorisch, wenn das zweifache Anwenden die Identität ist. Anschaulich: Zwei Mal machen macht gar nichts. Beispiele sind die komplexe Konjugation, die hermitesche Konjugation, das Transponieren, das Invertieren und viele mehr.
irrational
- siehe irrationale Zahlen
irreduzibel
- In einem Integritätsring R heißt eine von Null verschiedene Nichteinheit
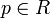 irreduzibel, wenn für alle
irreduzibel, wenn für alle 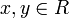 aus p = xy folgt: x ist eine Einheit oder y ist eine Einheit. Siehe auch irreduzibles Polynom.
aus p = xy folgt: x ist eine Einheit oder y ist eine Einheit. Siehe auch irreduzibles Polynom. - Eine lineare Darstellung heißt irreduzibel, wenn sie nicht reduzibel ist, wenn also der Vektorraum, in dem die Darstellung stattfindet, keine nichttrivialen Unterräume hat, die unter allen darstellenden Transformationen erhalten bleiben. Die Klassifikation nach irreduziblen Darstellungen ist die Hauptaufgabe der Darstellungstheorie.
- Eine Markow-Kette heißt irreduzibel, wenn jeder Zustand mit jedem verbunden ist.
- Irreduzibler topologischer Raum
irreflexiv
- Eine zweistellige Relation R heißt irreflexiv auf einer Menge, wenn kein Element dieser Menge in Relation zu sich selbst steht: ¬ ∃ x: xRx. „Irreflexiv“ ist somit nicht das Gegenteil von „reflexiv“: eine Relation kann ohne weiteres weder reflexiv noch irreflexiv sein. Die Relation auf der leeren Menge ist sowohl reflexiv als auch irreflexiv. Eine irreflexive Ordnungsrelation heißt strikt.
isometrisch isomorph
- Zwei metrische Räume heißen isometrisch isomorph, wenn sie durch eine bijektive Isometrie aufeinander abgebildet werden können.
isomorph
- Zwei Mengen heißen isomorph, wenn sie durch einen Isomorphismus, also eine bijektive strukturerhaltende Abbildung aufeinander abgebildet werden können.
isotrop
- Ein Element x eines Bilinearraumes (V, b) heißt isotrop, wenn die Gleichung b(x, x) = 0 gilt.
J
K
kanonisch
- Die kanonische Basis des Vektorraums R3 ist {(1,0,0), (0,1,0), (0,0,1)}. Achtung: nicht jeder Vektorraum hat eine kanonische Basis.
- Die kanonische Abbildung φ eines Vektorraums V auf einen Faktorraum V/U ist durch φ(v)=v+U gegeben.
- Beispiel kanonische Verknüpfung: Hat man eine einfache algebraische Struktur, wie etwa eine Menge M und eine Verknüpfung
 darauf, so kann man allgemein formulieren, wie sich eine Verknüpfung auf einer Quotientenmenge von M nach einer beliebigen Äquivalenzrelation R definieren lässt. Nämlich als Verknüpfung
darauf, so kann man allgemein formulieren, wie sich eine Verknüpfung auf einer Quotientenmenge von M nach einer beliebigen Äquivalenzrelation R definieren lässt. Nämlich als Verknüpfung 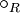 zwischen den Äquivalenzklassen, wobei sich das Ergebnis der Verknüpfung als die Äquivalenzklasse des Ergebnisses der Anwendung der ursprünglichen Verknüpfung auf je einen beliebigen Repräsentanten der zu verknüpfenden Klassen ergibt; für Elemente
zwischen den Äquivalenzklassen, wobei sich das Ergebnis der Verknüpfung als die Äquivalenzklasse des Ergebnisses der Anwendung der ursprünglichen Verknüpfung auf je einen beliebigen Repräsentanten der zu verknüpfenden Klassen ergibt; für Elemente 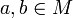 also
also ![[a] \circ_R [b] \stackrel{\text{def}}= [a \circ b].](/pictures/dewiki/98/b03e09c297e7e68aa77e07370445dfc0.png) Dies ist jedoch weder immer die einzige Möglichkeit eine Verknüpfung auf der Quotientenmenge zu definieren, noch ist sie immer wohldefiniert, führt also zu einem Ergebnis. Hier ist sie zum Beispiel nur wohldefiniert, wenn ursprüngliche Verknüpfung und betrachtete Äquivalenzrelation miteinander verträglich sind. Ist sie wohldefiniert, kann man die Verknüpfung als kanonische Verknüpfung bezeichnen.
Dies ist jedoch weder immer die einzige Möglichkeit eine Verknüpfung auf der Quotientenmenge zu definieren, noch ist sie immer wohldefiniert, führt also zu einem Ergebnis. Hier ist sie zum Beispiel nur wohldefiniert, wenn ursprüngliche Verknüpfung und betrachtete Äquivalenzrelation miteinander verträglich sind. Ist sie wohldefiniert, kann man die Verknüpfung als kanonische Verknüpfung bezeichnen. - Eine kanonische Transformation, in der klassischen Mechanik eine Koordinatentransformation im Phasenraum, die die Hamiltonschen Gleichungen invariant lässt.
- schwer zu fassender Begriff, der ungefähr soviel wie eindeutig analog bedeutet: Wird eine Eigenschaft (oder Methode) eines mathematischen Objektes aus den Eigenschaften und/oder Methoden eines anderen abgeleitet, indem eine Vorgehensweise angewendet wird, die analog zu einer Vorgehensweise ist, durch die bereits eine andere Eigenschaft (oder Methode) desselben mathematischen Objektes abgeleitet wurde, und ergibt sich die abgeleitete Eigenschaft (oder Methode) hierbei eindeutig, so kann die Eigenschaft (oder Methode) als kanonisch bezeichnet werden. Sie wird sozusagen analog zu der anderen Eigenschaft (oder Methode) für dasselbe Objekt abgeleitet und ergibt sich dabei eindeutig.
- Verwandte Begriffe: natürlich, standardisiert, normiert, üblich, gewöhnlich.
Klasse Cp
- eine Funktion ist von der Klasse Cp bzw. eine Cp-Funktion, wenn sie p mal stetig differenzierbar ist.
klein
- Eine Kategorie heißt klein, wenn die Klasse ihrer Objekte eine Menge ist.
kleinstes Element
- Ein Element x einer halbgeordneten Menge heißt kleinstes Element, wenn alle anderen Elemente größer sind, d. h. für jedes Element y die Relation x ≤ y gilt. Das kleinste Element einer halbgeordneten Menge existiert nicht immer, ist aber im Falle seiner Existenz eindeutig bestimmt. Siehe auch minimal und größtes.
kollinear
- Drei oder mehr Punkte, die auf einer Geraden liegen, heißen kollinear.
- Zwei Vektoren heißen kollinear, wenn sie linear abhängig sind.
- Eine Abbildung zwischen Vektorräumen, die alle Geraden wieder auf Geraden abbildet, heißt kollinear oder projektiv oder Kollineation. Siehe Kollineare Abbildung.
Kolmogoroffsch
- Ein topologischer Raum ist ein Kolmogoroff-Raum, wenn das Trennungsaxiom T0 gilt: zu jedem Paar von unterschiedlichen Punkten gibt es eine offene Menge, die einen Punkt enthält, jedoch nicht den anderen.
kommutativ
- Eine zweistellige Verknüpfung · heißt kommutativ, wenn x·y = y·x (das Kommutativgesetz) für alle x und y gilt.
- Eine Gruppe heißt kommutativ (auch: abelsch), wenn ihre Verknüpfung kommutativ ist.
- Ein Ring heißt kommutativ, wenn die Multiplikation kommutativ ist.
- Ein Diagramm heißt kommutativ, wenn verschiedene Pfade zwischen je zwei Punkten des Diagramms zu gleichen Funktionen führen.
kompakt
- Ein topologischer Raum ist kompakt, falls jede offene Abdeckung eine endliche Unterabdeckung besitzt. Kompakte Räume sind immer lindelöf und parakompakt. Kompakte Hausdorff-Räume sind somit normal.
- (aus der obigen Definition folgt:) Eine Teilmenge M eines metrischen Raumes ist kompakt, wenn jede Folge in M eine in M konvergente Teilfolge besitzt.
- Ein linearer Operator zwischen normierten Räumen heißt kompakt, falls das Bild der Einheitkugel einen kompakten Abschluss hat.
komplanar
- Eine Gerade heißt komplanar zu einer Ebene, wenn sie zu ihr parallel ist oder einer Teilmenge von ihr entspricht. Die Richtungsvektoren der Gerade und der Ebene sind dann linear abhängig.
komplementär
- Zwei spitze Winkel heißen komplementär oder Komplementwinkel, wenn sie sich zu einem rechten Winkel (90°) ergänzen
- siehe auch: Minor
konform
- Eine Abbildung f aus einem Gebiet G in die komplexe Ebene C heißt lokal konform, wenn sie reell differenzierbar und winkeltreu (orientierungserhaltend) ist, d. h. das Differential ist für alle Elemente des Gebiets eine Drehstreckung (die Cauchy-Riemannschen Differentialgleichungen gelten). Mit anderen Worten: f ist lokal konform, wenn f analytisch auf einem Gebiet G ist und die Ableitung von f für jedes Element aus G von Null verschieden ist.
- Ist f lokal konform und bijektiv, so heißt f konform.
- Wenn f konform ist, so ist es auch die Umkehrabbildung
- Siehe hierzu: Konforme Abbildung
kongruent
- Zwei geometrische Figuren heißen kongruent oder deckungsgleich, wenn sie durch Verschiebung, Drehung und Spiegelung aufeinander abgebildet werden können. Siehe Kongruenz (Geometrie). Wird zusätzlich zentrische Streckung zugelassen, heißen die Figuren ähnlich.
- In Algebra und Zahlentheorie heißen zwei Zahlen kongruent modulo m, wenn sie denselben Rest bezüglich eines Divisors m haben. Beispiel: 3 ≡ 24 mod 7. Siehe Kongruenz (Zahlentheorie).
konjugiert
- Zwei Komplexe Zahlen a und b heißen konjugiert komplex zueinander, wenn ihre Realteile übereinstimmen und ihre Imaginärteile gleichen Betrag und unterschiedliches Vorzeichen haben. Beispiel: die komplex Konjugierte von 2+i ist 2−i.
- Matrizen heißen komplex konjugiert zueinander, wenn alle ihre Koeffizienten komplex konjugiert zueinander sind.
- In der Funktionalanalysis heißen lineare Operatoren komplex konjugiert zueinander, wenn …
- In der abstrakten Algebra heißen zwei über K algebraische Elemente einer Körpererweiterung L/K zueinander konjugiert, wenn sie dasselbe Minimalpolynom über K haben. Die Nullstellen des Minimalpolynoms von a in L heißen Konjugierte von a (in L). Jeder K-Automorphismus von L (der K punktweise festhält) bildet a auf eine seiner Konjugierten ab.
- In einer Gruppe (G, *) heißen die Elemente a und b zueinander konjugiert, wenn es ein Gruppenelement c gibt, sodass b = c − 1ac ist. Die Abbildung
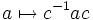 heißt Konjugation mit c.
heißt Konjugation mit c. - Zwei Untergruppen U und V heißen zueinander konjugiert, wenn es ein Element c gibt, sodass cU = Vc.
- Zwei Zahlen
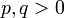 heißen konjugiert, wenn
heißen konjugiert, wenn 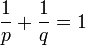 gilt.
gilt. - Zwei stetige Abbildungen
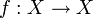 sowie
sowie 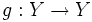 bezüglich zweier metrischer Räume X und Y heißen topologisch konjugiert, wenn es einen Homöomorphismus
bezüglich zweier metrischer Räume X und Y heißen topologisch konjugiert, wenn es einen Homöomorphismus 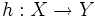 gibt sodass:
gibt sodass: 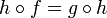 .
.
konsistent
- In der mathematischen Statistik heißt eine Schätzung konsistent, wenn sie in Wahrscheinlichkeit (d. h. für eine ins Unendliche wachsende Stichprobe) gegen die geschätzte Größe konvergiert.
konvex
- Eine Menge eines reellen Vektorraums heißt konvex, wenn sie mit je zwei Punkten auch die Verbindungsstrecke enthält.
- Eine auf einer konvexen Menge K definierte reellwertige Funktion f heißt (von unten) konvex, wenn
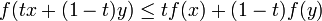 für alle
für alle 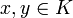 und alle
und alle ![t\in [0,1]](/pictures/dewiki/100/d9a06fde4663cdd5b1ba693e9127232f.png) (das heißt, der Funktionsgraph verläuft stets unterhalb jeder Sekante).
(das heißt, der Funktionsgraph verläuft stets unterhalb jeder Sekante).
kopunktal
- Drei oder mehr Geraden, die durch einen gemeinsamen Punkt gehen (mit demselben Punkt inzidieren).
L
lindelöf
- Ein topologischer Raum ist ein Lindelöf-Raum, falls jede offene Abdeckung (auch „Überdeckung“) eine abzählbare Unterabdeckung besitzt. Nach dem Mathematiker Ernst Leonard Lindelöf.
linear
- Eine Funktion der Form f(x) = a + bx heißt affin-linear, siehe auch affine Abbildung und lineare Funktion. In der Elementarmathematik und vielen Anwendungen sagt man stattdessen nur linear. Das ist mit der folgenden, in weiten Teilen der Mathematik üblichen Definition von linear nur im Sonderfall a=0 kompatibel:
- In der Algebra und darauf zurückgreifenden Gebieten der Mathematik heißt ein funktionaler Zusammenhang f(x) linear, wenn er folgende zwei Bedingungen erfüllt: (1) Additivität: f(x + y) = f(x) + f(y); (2) Homogenität: f(αx) = αf(x) für alle α aus einem zugrunde liegenden Körper.
- In der Logik heißen Terme linear, wenn sie jede Variable höchstens einmal enthalten.
- Die Funktionalanalysis handelt von linearen Operatoren.
- Eine lineare Ordnungsrelation heißt auch total, siehe dort.
- In der Codierungstheorie heißt ein Code linear, wenn er die Struktur eines Vektorraumes trägt.
linksgekrümmt
Eine zwei Mal differenzierbare Funktion
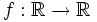 heißt in einem Intervall
heißt in einem Intervall 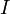 linksgekrümmt, wenn die zweite Ableitung positiv ist, also
linksgekrümmt, wenn die zweite Ableitung positiv ist, also 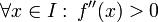 . Der Name rührt daher, dass ein Fahrzeug stets nach links lenken muss, wenn es sich in Richtung steigender
. Der Name rührt daher, dass ein Fahrzeug stets nach links lenken muss, wenn es sich in Richtung steigender 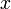 -Werte entlang des Graphen der Funktion bewegt. Linksgekrümmte Funktionen sind streng konvex.
-Werte entlang des Graphen der Funktion bewegt. Linksgekrümmte Funktionen sind streng konvex.linksverträglich
- Siehe verträglich
Lipschitz-stetig
Eine reelle Funktion heißt Lipschitz-stetig, wenn die Anstiege (oder „Steigungen“) aller Sekanten nach oben und unten beschränkt sind. Der Begriff kann auf Funktionen in metrischen Räumen ausgedehnt werden.
lokal
- auf eine Umgebung bezogen
- Ein Ring heißt lokal, wenn er genau ein maximales Linksideal (oder Rechtsideal) besitzt.
lokal endlich
- Ein System von Teilmengen eines topologischen Raums ist lokal endlich, falls jeder Punkt eine Umgebung hat, die nur endlich viele der Teilmengen berührt.
- Eine Halbordnung
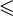 auf einer Mengen M ist lokal endlich, wenn jedes Intervall
auf einer Mengen M ist lokal endlich, wenn jedes Intervall ![[x,y]=\{z\in M:x\leqslant z\leqslant y\}](/pictures/dewiki/56/8d9b2a6632cfa0df179f5b5683c89190.png) eine endliche Menge ist.
eine endliche Menge ist.
lokal Lipschitz-stetig
Eine reelle Funktion heißt lokal Lipschitz-stetig, wenn die Anstiege aller Sekanten nach oben und unten, innerhalb eines Intervalls, beschränkt sind.
lokal metrisierbar
- Ein topologischer Raum ist lokal metrisierbar, falls jeder Punkt eine metrisierbare Umgebung besitzt.
lokal zusammenhängend
M
mager
- Als magere Menge wird eine Teilmenge eines topologischen Raums X bezeichnet, die als abzählbare Vereinigung nirgends dichter Teilmengen von X darstellbar ist. Siehe dazu Satz von Baire.
marginal
- In der Stochastik heißt eine Wahrscheinlichkeit marginal, die aus einer bedingten Wahrscheinlichkeit durch „Marginalisierung“ hervorgegangen ist. „Marginalisieren“ heißt, über alle möglichen Werte einer Bedingung zu summieren oder integrieren. Beispiel: Ausgehend von der bedingten Wahrscheinlichkeit P(A|B,C) ist P(A|B) bezüglich C marginal.
maximal
- Ein Element einer halbgeordneten Menge heißt maximal, wenn es in der Ordnung kein größeres Element gibt. Dieses Element muss nicht das größte Element sein: Wenn es mehrere maximale Elemente gibt, gibt es kein größtes.
- Ideal (Mathematik), Untermodul
- Ein Orthonormalsystem S eines Hilbertraums H heißt maximal, wenn es in H außer dem Nullvektor keinen Vektor gibt, der zu allen Vektoren aus S orthogonal ist. Das heißt, es gilt für alle x aus H
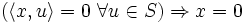 .
.
meromorph
- Ist (eine Funktion einer komplexen Variablen) f holomorph im Gebiet G bis auf eventuelle Ausnahme von Polen, so heißt f meromorph in G.
messbar
- Messbarer Raum wäre die wörtliche Übersetzung des englischen measurable space, der auf Deutsch eingeführterweise Messraum heißt; siehe Maßtheorie. Die einzelnen Mengen der σ-Algebra eines Maßraums (d. h. eines Messraums, auf dem ein Maß definiert ist) heißen jedenfalls messbar; siehe auch dazu den Artikel Maßtheorie.
- Messbar ist nicht das gleiche wie metrisierbar, da ein Maß keine Metrik ist.
metrisierbar
- Ein topologischer Raum ist metrisierbar, falls er homöomorph zu einem metrischen Raum ist. Metrisierbare Räume sind immer Hausdorff’sch und parakompakt (und daher normal und Tychonoff’sch) und erst-abzählbar).
minimal
- Ein Element einer halbgeordneten Menge heißt minimal, wenn es in der Ordnung kein kleineres Element gibt. Dieses Element muss nicht das kleinste Element sein: Wenn es mehrere minimale Elemente gibt, gibt es kein kleinstes.
monoton
- Folgen. Eine Folge von Elementen einer geordneten Menge heißt monoton wachsend bzw. monoton abnehmend, wenn jedes Folgenglied kleiner bzw. größer ist als das nächste. Eine Folge heißt monoton, wenn sie monoton wachsend oder monoton abnehmend ist.
- Logik
- Eine Schauderbasis heißt monoton, wenn die Basiskonstante 1 ist.
multilinear
- Eine Abbildung die Argumente aus mehreren Vektorräumen in einen Vektorraum abbildet, heißt multilinear, wenn sie in jedem Argument linear ist, wobei alle Vektorräume über demselben Skalarkörper definiert sein müssen. Eine multilineare Abbildung in den Skalarkörper ist eine Multilinearform.
multiplikativ
- Man nennt eine Gruppe oder Halbgruppe multiplikativ (im Gegensazu zu additiv), wenn das verwendete Symbol für die Gruppenverknüpfung ein Punkt ist bzw. weggelassen wird. Der Begriff bezieht sich ausschließlich auf die Schreibweise. Das neutrale Element wird dann häufig als Einselement und mit 1 oder e bezeichnet, das Inverse von a mit a − 1 und die n-fache Verknüpfung eines Elements mit sich selbst wird als Potenz an geschrieben.
- Eine Abbildung zwischen zwei Strukturen mit einer multiplikativen Verknüpfung heißt multiplikativ, wenn sie bezüglich dieser Verknüpfung ein Homomorphismus ist. So werden z. B. bei der Gelfand-Transformation multiplikative, lineare Funktionale auf einer Banachalgebra betrachtet. Vergleiche auch Multiplikativität der Norm oder Multiplikativität der Determinante.
- In der Zahlentheorie nennt man eine auf den natürlichen Zahlen definierte Abbildung f multiplikativ, wenn f(nm) = f(n)f(m) für je zwei teilerfremde Zahlen n und m gilt, siehe Zahlentheoretische Funktionen.
multivariat
- Eine Funktion ist multivariat, wenn sie mehrere unbestimmte Variablen enthält (z. B. 3x2y + y2z − x2z3). Siehe auch: univariat.
- Die gemeinsame Verteilung mehrerer Zufallsvariablen ist multivariat (s. Hauptartikel: multivariate Verteilung). Ebenso ist die gemeinsame Analyse mehrerer statistischer Merkmale multivariat (s. Hauptartikel: multivariate Verfahren).
N
natürlich
- Eine Abbildung zwischen zwei Konstruktionen F(A) und G(A) zu einem Objekt heißt natürlich, wenn sie kompatibel mit dem Austausch von A durch andere Objekte ist. Beispiel: die Determinante als Abbildung der n × n-Matrizen in den Grundkörper ist kompatibel mit dem Übergang zu einem Erweiterungskörper. Siehe Kategorientheorie
- Siehe natürliche Zahl
- Siehe natürlicher Logarithmus
negativ
- Eine reelle Zahl heißt negativ, wenn sie kleiner als Null ist. Eine Zahl, die kleiner oder gleich Null ist, bezeichnet man am kürzesten als nicht-positiv. Siehe positive und negative Zahlen.
negativ definit
- Eine reelle symmetrische oder komplexe hermitesche Bilinearform s:V×V→K heißt negativ definit, wenn s(v,v) < 0 für alle v aus V\{0}. Siehe auch positiv definit.
nilpotent
- Ein Endomorphismus f eines Vektorraums oder eine quadratische Matrix A heißen nilpotent, wenn es eine Zahl p≥1 gibt, sodass fp=0 bzw. Ap=0, siehe nilpotente Matrix, nilpotentes Element.
- Nilpotente Gruppe
nirgends dicht oder nirgendwo dicht
- Eine Teilmenge eines topologischen Raums ist nirgends dicht, wenn das Innere ihres Abschlusses leer ist. Beispiel: die Menge der ganzen Zahlen
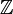 ist nirgends dicht in der Menge der reellen Zahlen
ist nirgends dicht in der Menge der reellen Zahlen 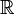 .
.
normal
- In der Geometrie, insbesondere in der analytischen Geometrie, heißt eine Gerade normal zu einer Ebene (allgemeiner zu einer Fläche), wenn sie senkrecht auf dieser steht.
- In der Topologie heißt ein topologischer Raum normal, falls beliebige zwei disjunkte abgeschlossene Mengen disjunkte Umgebungen haben. Normale Räume erlauben Zerlegungen der Eins. Normale T1-Räume sind immer Tychonoff-Räume.
- In der Statistik ist eine Zufallsvariable normal, wenn sie normalverteilt (Gauß-verteilt) ist.
- In der Gruppentheorie sagt man im Deutschen statt normale Untergruppe üblicherweise Normalteiler. Ein Normalteiler ist invariant unter Konjugation beliebiger Gruppenelemente.
- In der Körpertheorie ist eine endliche Körpererweiterung L | K normal, wenn jedes irreduzible Polynom über K, das eine Nullstelle in L hat, dort in Linearfaktoren zerfällt. Äquivalent dazu ist, dass das Bild einer Einbettung
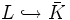 in einen algebraischen Abschluss von K nicht von der Einbettung abhängt. Beispiel:
in einen algebraischen Abschluss von K nicht von der Einbettung abhängt. Beispiel: ![\mathbb Q(\sqrt[3]2)|\mathbb Q](/pictures/dewiki/51/3432f1b8e72ce26863975d7a9dd56da5.png) ist nicht normal.
ist nicht normal. - In der kommutativen Algebra heißt ein Ring normal, wenn er nullteilerfrei und ganzabgeschlossen in seinem Quotientenkörper ist oder diese Bedingung für alle lokalen Ringe erfüllt ist. Beispiel:
![\mathbb Z[\sqrt5]](/pictures/dewiki/101/eda3c039b3c1230e72ac79bdb72d38d2.png) ist nicht normal, der ganze Abschluss im Quotientenkörper
ist nicht normal, der ganze Abschluss im Quotientenkörper 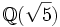 ist
ist ![\mathbb Z\!\left[\frac{1+\sqrt5}2\right].](/pictures/dewiki/102/f632f6672eab286873f00dfeea28628f.png)
- In der linearen Algebra heißt eine Matrix A normal, wenn sie mit ihrer komplex konjugierten Transponierten (hermitesch Adjungierten) kommutiert,
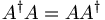 .
. - In der Funktionalanalysis heißt ein linearer Operator in einem Hilbert-Raum normal, wenn er mit seinem adjungierten Operator kommutiert.
- Eine reelle Zahl heißt normal, wenn unter ihren Nachkommaziffern für jedes
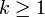 alle möglichen k-stelligen Ziffernblöcke mit gleichen asymptotischen relativen Häufigkeiten auftreten.
alle möglichen k-stelligen Ziffernblöcke mit gleichen asymptotischen relativen Häufigkeiten auftreten.
normiert
- Ein Vektor heißt normiert oder Einheitsvektor, wenn er die Norm 1 hat.
- (auch: normalisiert): Ein normierter Wertebereich einer Variablen ist auf einen bestimmten Bereich skaliert – üblicherweise zwischen 0 und 1 (bzw. 100 Prozent).
- Ein Polynom nennt man normiert, wenn der Leitkoeffizient (der Koeffizient der höchsten Potenz der Variable) 1 ist.
- Ein Normierter Raum ist ein Vektorraum, der mit einer Norm ausgestattet ist.
- Eine Gleichung heißt normiert, wenn sie auf grundlegende Funktionen zurückgeführt oder in eine bestimmte standardisierte Darstellung gebracht ist.
normalisiert
- (auch: normiert): Ein normierter Wertebereich einer Variablen ist auf einen bestimmten Bereich skaliert – üblicherweise zwischen 0 und 1 (bzw. 100 Prozent).
notwendig
- Eine Aussage A ist eine notwendige Bedingung einer anderen Aussage B, wenn zwischen den beiden Aussagen die logische Beziehung „aus B folgt A“ (kurz: B ⇒ A) besteht. Äquivalent dazu ist die Implikation „nicht A ⇒ nicht B“. Der Gegenbegriff ist hinreichend. Siehe hierzu auch Notwendige und hinreichende Bedingung.
nullhomolog
- Eine im Gebiet
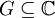 geschlossene Kurve
geschlossene Kurve ![\alpha:[a,b]\to G](/pictures/dewiki/98/b566b0830c0119ce445ac22a1dcfbc3b.png) , heißt nullhomolog in G, wenn ihr Inneres
, heißt nullhomolog in G, wenn ihr Inneres 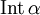 vollständig in G liegt, wobei
vollständig in G liegt, wobei ![\operatorname{Int}\,\alpha:=\{z\in\mathbb C\setminus\alpha([a,b]): n(\alpha,z)\ne 0\}](/pictures/dewiki/51/30952a2d7c9f99ddc5188cbc3b4b942d.png) mit der Windungszahl n.
mit der Windungszahl n.
nullhomotop
- Eine geschlossene Kurve
![\alpha, \alpha:[a,b]\to D](/pictures/dewiki/97/ae50dcac92f3daa5509288792c6e284b.png) , heißt nullhomotop, wenn sie homotop zur konstanten Kurve
, heißt nullhomotop, wenn sie homotop zur konstanten Kurve ![\beta:[a,b]\to D](/pictures/dewiki/54/63b8598f123699d0adb25b5f2c2b92b1.png) mit β(t) = α(a) = α(b) für alle t ist, also zu einer „Kurve“, die in einen Punkt ausgeartet ist. Jede in einem Gebiet G nullhomotope Kurve ist auch in G nullhomolog. Die Umkehrung gilt im Allgemeinen nicht.
mit β(t) = α(a) = α(b) für alle t ist, also zu einer „Kurve“, die in einen Punkt ausgeartet ist. Jede in einem Gebiet G nullhomotope Kurve ist auch in G nullhomolog. Die Umkehrung gilt im Allgemeinen nicht.
numerisch
- Eine Funktion
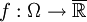 mit
mit 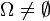 heißt numerisch.
heißt numerisch. 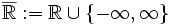 bezeichnet dabei die erweiterten reellen Zahlen.
bezeichnet dabei die erweiterten reellen Zahlen.
O
orientiert
Der Begriff der Orientierung lässt sich für endlichdimensionale Vektorräume über geordneten Körpern definieren und verallgemeinert das Konzept
- der Durchlaufrichtung im Eindimensionalen,
- der Begriffe links und rechts sowie des Drehsinns in der Ebene,
- der Begriffe Linkssystem und Rechtssystem im dreidimensionalen Raum (vgl. Daumen, Zeigefinger und Mittelfinger der linken bzw. rechten Hand).
Im n-dimensionalen Raum ist die Orientierung eine Eigenschaft der Basen. Zwei Basen (aus n linear unabhängigen Vektoren in gegebener Reihenfolge) heißen äquivalent, wenn sie durch eine lineare Abbildung positiver Determinante auseinander hervorgehen. Es gibt genau zwei Äquivalenzklassen, die Orientierungen, nämlich die positive und die negative Orientierung. Dabei ist die kanonische Basis positiv orientiert.
offen
- Auf der reellen Zahlengerade heißt ein Intervall I: = ]a,b[ = (a,b) offen, wenn es durch
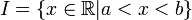 gegeben ist.
gegeben ist. - Welche Teilmengen eines topologischen Raums offen heißen, ist Teil der Struktur eines topologischen Raumes. Aus einer Menge wird ein topologischer Raum dadurch, dass man angibt, welche Teilmengen offen heißen sollen.
- Eine Menge, die Umgebung aller ihrer Punkte ist, heißt offen.
- Eine Abbildung zwischen zwei topologischen Räumen heißt offen, wenn sie offene Mengen auf offene Mengen abbildet.
Ordnung
- Die Ordnung einer Gruppe ist die Anzahl ihrer Elemente (die Mächtigkeit der der Gruppe zugrunde liegenden Menge).
- In der Gruppentheorie ist die Ordnung n eines Gruppenelements g die kleinste positive ganze Zahl, für die gn=e gilt (mit dem neutralen Element e).
- Die Ordnung einer Nullstelle oder einer Polstelle ist deren Vielfachheit.
- Die Ordnung einer Differentialgleichung ist der höchste vorkommende Ableitungsgrad.
- Die Ordnung eines Terms, mit einem Landau-Symbol O(x) bezeichnet, beschreibt die Geschwindigkeit, mit der dieser Term in einem Grenzübergang divergiert.
- Ordnung kann außerdem Anordnung bedeuten, also die durch eine Ordnungsrelation induzierte Struktur bezeichnen.
- In der algebraischen Zahlentheorie heißt ein Unterring O des Ganzzahlringes eines Zahlkörpers K eine Ordnung, wenn O eine Ganzheitsbasis der Länge
![[K:\mathbb Q]](/pictures/dewiki/49/193364dbf885efd2be217a886977b370.png) besitzt.
besitzt.
ordnungstreu
- Eine Abbildung F: A→B der geordneten Klasse (A, <A) auf der geordneten Klasse (B, <B) heißt ordnungstreu, wenn
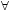 a,b
a,b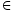 A: a <A b
A: a <A b 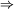 F(a) <B F(b).
F(a) <B F(b).
ordnungsvollständig
Eine Menge mit einer Ordnungsrelation heißt ordnungsvollständig, wenn jede nach oben beschränkte Teilmenge ein Supremum hat. Siehe Ordnungstopologie.
orthogonal
- In der Geometrie sind zwei Geraden oder Ebenen orthogonal zueinander, wenn sie einen rechten Winkel bilden.
- Ein Koordinatensystem heißt orthogonal, wenn seine Achsen paarweise orthogonal zueinander sind.
- Eine Projektion heißt orthogonal, wenn die Projektionsstrahlen senkrecht auf die Projektionsflläche treffen.
- In der linearen Algebra und analytischen Geometrie sind zwei Vektoren orthogonal zueinander, wenn ihr Skalarprodukt null ist.
- Da in der Funktionalanalysis Funktionen als Vektoren aufgefasst werden, folgt unmittelbar, dass zwei Funktionen f und g orthogonal zueinander heißen, wenn ihr inneres Produkt null ist; das innere Produkt in Funktionenräumen ist in der Regel definiert als Integral von f*(x)g(x), gegebenenfalls multipliziert mit einer Gewichtsfunktion w(x).
- Eine quadratische Matrix A heißt orthogonal, wenn ihre Inverse A−1 mit ihrer Transponierten AT übereinstimmt, wenn also A AT = AT A = 1. Siehe: orthogonale Matrix. Orthogonale Matrizen besitzen in aller Regel reelle Koeffizienten. Matrizen mit komplexen Koeffizienten, die analoge Symmetrieeigenschaften besitzen, heißen unitär; die Transposition wird dabei durch die hermitesche Konjugation ersetzt.
- Die Menge aller orthogonalen Matrizen vom Rang n über dem Körper K heißt orthogonale Gruppe O(n,K).
orthonormal
- „Orthonormal“ ist ein Kunstwort aus „orthogonal“ (s. o.) und „normiert“, d. h. zwei Vektoren sind genau dann orthonormal zueinander (bzw. bilden dann ein so genanntes Orthonormalensystem), wenn sie orthogonal stehen und die Vektoren Einheitsvektoren sind (Vektoren der Länge 1).
P
paarweise verschieden
- je zwei Elemente einer Aufzählung sind verschieden, z. B. 1, 2, 3
- 1, 1, 2 sind verschiedene Elemente, aber nicht paarweise verschieden
parabolisch
- In der Geometrie ist eine Parabel eine Kurve zweiten Grades.
- Eine fundamentale Klasse partieller Differentialgleichungen heißt parabolisch.
parakompakt
- Ein topologischer Raum ist parakompakt, falls jede offene Überdeckung eine offene, lokal endliche Verfeinerung besitzt. Parakompakte Hausdorff-Räume sind normal.
perfekt
- In der Zahlentheorie heißen natürliche Zahlen perfekt (auch „vollkommen“), wenn sie gleich der Summe ihrer echten Teiler sind. Beispiel: 6=1+2+3. Ob es ungerade perfekte Zahlen gibt, ist bis heute unbekannt. Siehe vollkommene Zahl.
- In der Topologie heißt eine Menge perfekt, wenn sie abgeschlossen ist und jeder ihrer Punkte ein Häufungspunkt der Menge ist (s. Hauptartikel: Häufungspunkt).
polnisch
- Ein topologischer Raum X heißt polnisch, wenn er separabel und vollständig metrisierbar ist.
positiv
- Eine reelle Zahl heißt nach vorherrschendem Sprachgebrauch positiv, wenn sie größer als Null ist. Zahlen, die größer oder gleich Null sind, werden am kürzesten als nicht-negativ bezeichnet. Siehe positive und negative Zahlen.
positiv definit
- Eine reelle symmetrische oder komplexe hermitesche Bilinearform s:V×V→K heißt positiv definit, wenn s(v,v) > 0 für alle v aus V\{0}.
- Eine Matrix
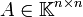 heißt positiv definit, falls
heißt positiv definit, falls 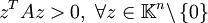 . Ist
. Ist 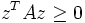 , so bezeichnet man A als positiv semidefinit. In der Anwendung gilt meistens
, so bezeichnet man A als positiv semidefinit. In der Anwendung gilt meistens 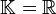 oder
oder 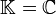 .
. - Siehe auch negativ definit.
präkompakt
- Siehe total beschränkt oder relativ kompakt
prim
- Eine natürliche Zahl heißt prim oder eine Primzahl, wenn sie außer den beiden trivialen Teilern (die Zahl selbst und die 1) keine weiteren Teiler besitzt. Die Zahlen 0 und 1 werden ausgeschlossen und sind keine Primzahlen.
- Allgemein heißt ein Element eines Integritätsrings prim, wenn es ungleich 0 und keine Einheit ist, und als Teiler eines Produkts auch immer einen der Faktoren teilt.
primitiv
- Ein Polynom
![f \in R[X]](/pictures/dewiki/97/abd35e6da207283b3a043689ec2a8e66.png) über einem faktoriellen Ring R heißt primitiv, wenn sein Inhalt eine Einheit ist, wenn also die Koeffizienten des Polynoms teilerfremd sind.
über einem faktoriellen Ring R heißt primitiv, wenn sein Inhalt eine Einheit ist, wenn also die Koeffizienten des Polynoms teilerfremd sind. - Ein normiertes irreduzibles Polynom
![p(x) \in F_q[x]](/pictures/dewiki/102/f47ecdcc2995d8d018ec1e7338df475f.png) vom Grad n über einem endlichen Körper Fq, dessen Wurzeln im Zerfällungskörper
vom Grad n über einem endlichen Körper Fq, dessen Wurzeln im Zerfällungskörper 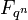 über Fq primitive Elemente sind, heißt primitives Polynom.
über Fq primitive Elemente sind, heißt primitives Polynom. - Ein erzeugendes Element einer einfachen Körpererweiterung heißt primitives Element des Erweiterungskörpers. Zum Beispiel ist
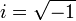 das primitive Element der einfachen Körpererweiterung
das primitive Element der einfachen Körpererweiterung 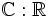 .
. - Ein erzeugendes Element der multiplikativen, zyklischen Gruppe F * eines endlichen Körpers F heißt primitives Element des Körpers F.
projektiv
- Siehe Projektive Geometrie, Projektive Abbildung
- Ein Objekt P einer Kategorie heißt projektiv, wenn sich Morphismen mit Quelle P entlang von Epimorphismen hochheben lassen.
- Das projektive Tensorprodukt ist eine spezielle Variante des Tensorproduktes normierter oder lokalkonvexer Räume.
punktweise
- Sind A und B (nichtleere) Mengen, und ist F eine Familie von Abbildungen
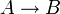 , so gilt eine Eigenschaft punktweise auf F, wenn für jeden Punkt
, so gilt eine Eigenschaft punktweise auf F, wenn für jeden Punkt 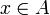 die Menge
die Menge 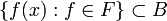 diese Eigenschaft besitzt. Beispiel: punktweise Konvergenz.
diese Eigenschaft besitzt. Beispiel: punktweise Konvergenz. - Ist F eine Familie von Funktionen von einer Menge M in eine algebraische Struktur S, so kann man aus den Verknüpfungen von S durch punktweise Definition entsprechende Verknüpfungen auf F definieren. Ist z.B.
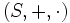 ein Körper, so kann man mit den Gleichung (f + g)(x): = f(x) + g(x) für
ein Körper, so kann man mit den Gleichung (f + g)(x): = f(x) + g(x) für 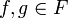 und
und 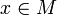 , punktweise eine Addition von Funktionen definieren. Ist F bzgl. dieser zweistelligen Verknüpfung abgeschlossen, so wird (F, + ) hierdurch zu einer abelschen Gruppe. Ebenso definiert man punktweise (λf)(x): = λf(x), für
, punktweise eine Addition von Funktionen definieren. Ist F bzgl. dieser zweistelligen Verknüpfung abgeschlossen, so wird (F, + ) hierdurch zu einer abelschen Gruppe. Ebenso definiert man punktweise (λf)(x): = λf(x), für 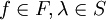 und
und 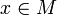 , womit dann F – wieder Abgeschlossenheit vorausgesetzt – zu einem Vektorraum über S. Definiert man zusätzlich, wieder punktweise, durch (fg)(x): = f(x)g(x) eine Multiplikation, und bleibt F auch unter dieser neuen Verknüpfung abgeschlossen, so wird F zu einer S-Algebra.
, womit dann F – wieder Abgeschlossenheit vorausgesetzt – zu einem Vektorraum über S. Definiert man zusätzlich, wieder punktweise, durch (fg)(x): = f(x)g(x) eine Multiplikation, und bleibt F auch unter dieser neuen Verknüpfung abgeschlossen, so wird F zu einer S-Algebra.
pythagoreisch
- Ein Pythagoreisches Tripel sind drei natürliche Zahlen x,y,z, welche die aus dem Satz des Pythagoras bekannte Gleichung x2 + y2 = z2 erfüllen. Beispiele: 3,4,5; 5,12,13. Siehe Pythagoreisches Tripel. Man findet pythagoreische Tripel durch den Ansatz x = a2 − b2, y = 2ab, z = a2 + b2.
Q
quasi-
Das Präfix Quasi- oder quasi- wird verwendet, um eine Eigenschaft zu charakterisieren, die – in einem streng definierten Sinne – „fast“ einer anderen entspricht oder einer anderen sehr „ähnlich“ ist.
Beispiele: Quasigruppe, Quasiordnung, quasikonforme Abbildung, quasikonkave Funktion, quasitonnelierter Raum, quasi-kompakt, Quasivollständigkeit.
R
Rang
- In der linearen Algebra ist der Rang einer linearen Abbildung die Dimension des Bildraums. Der Rang einer Matrix ist der Rang der durch die Matrix vermittelten linearen Abbildung.
- Der Rang eines Tensors, auch Stufe genannt, ist die Anzahl der Vektorräume, aus deren direktem Produkt der Tensor gebildet ist.
- In Anlehnung an den Rang eines Tensors ist in der Informatik, jedenfalls in der Fachsprache von Fortran, der Rang eines Feldes (Arrays) die Anzahl seiner Indizes.
- Der Rang einer abelschen Gruppe gibt die „Größe“ der Gruppe im Verhältnis zum Vektorraum über den rationalen Zahlen an.
rational
- Eine rationale Zahl ist eine Zahl, die sich als Quotient aus zwei ganzen Zahlen darstellen lässt.
- Die rationalen Funktionen über einem Körper K sind die Elemente des Quotientenkörpers des Polynomringes über K.
- Ein rationaler Baum ist ein möglicherweise unendlicher gerichteter Baum, der aber nur endlich viele verschiedene Unterbäume enthält.
- n Zahlen a1,...,an heißen rational abhängig, wenn es ganze Zahlen c1,...,cn gibt, die nicht alle gleich Null sind, sodass c1a1 + ... + cnan = 0.
rechtsgekrümmt
Eine zwei Mal differenzierbare Funktion
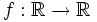 heißt in einem Intervall
heißt in einem Intervall 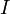 rechtsgekrümmt, wenn die zweite Ableitung negativ ist, also
rechtsgekrümmt, wenn die zweite Ableitung negativ ist, also 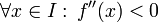 . Der Name rührt daher, dass ein Fahrzeug stets nach rechts lenken muss, wenn es sich in Richtung steigender
. Der Name rührt daher, dass ein Fahrzeug stets nach rechts lenken muss, wenn es sich in Richtung steigender 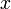 -Werte entlang des Graphen der Funktion bewegt. Rechtsgekrümmte Funktionen sind streng konkav.
-Werte entlang des Graphen der Funktion bewegt. Rechtsgekrümmte Funktionen sind streng konkav.rechtsverträglich
- Siehe verträglich
reduzibel
- Eine lineare Darstellung heißt reduzibel, wenn der Vektorraum, in dem die Darstellung stattfindet, nichttriviale Unterräume hat, die unter allen darstellenden Transformationen erhalten bleiben. Eine reduzible Darstellung kann in eine direkte Summe aus irreduziblen Darstellungen ausreduziert werden.
- Ringtheorie: reduzibles Element
reell
- Der Körper der reellen Zahlen entsteht durch Erweiterung aus dem der rationalen Zahlen durch Vervollständigung, etwa mit Hilfe der Äquivalenzklassen von Cauchy-Folgen oder aber der Dedekindschen Schnitte.
- Natürliche, ganze, rationale und reelle Zahlen sind alle reell.
- Komplexe Zahlen sind reell, wenn ihr Imaginärteil Null ist.
- Eine Matrix ist reell, wenn ihre sämtlichen Koeffizienten reell sind.
- Ein Körper heißt formal reell, wenn sein Element −1 nicht als Summe von Quadraten darstellbar ist.
reflexiv
- Eine zweistellige Relation R heißt reflexiv, wenn jedes Element in Relation zu sich selbst steht: ∀ x: xRx. Wenn kein Element in Relation zu sich selbst steht, heißt die Relation irreflexiv.
- Ein Banachraum heißt reflexiv, wenn die kanonische Einbettung in den Bidualraum surjektiv ist.
regelmäßig
- In der Geometrie heißen gleichseitige, gleichwinklige Vielecke und gleichflächige Polyeder (Platonische Körper) regelmäßig.
regulär
- In der Geometrie werden regelmäßige Vielecke und Körper auch regulär genannt.
- Eine parametrisierte differenzierbare Kurve heißt regulär, falls ihre Ableitung nach dem Parameter in keinem Punkt verschwindet.
- In der Topologie heißt ein topologischer Raum regulär, wenn jede Umgebung eines Punkts eine abgeschlossene Umgebung desselben Punkts enthält. Äquivalent dazu ist die Bedingung, dass alle abgeschlossenen Mengen C und Punkte p, die nicht in C liegen, disjunkte Umgebungen besitzen. Siehe Regulärer Raum. Reguläre T0-Räume sind immer Hausdorff’sch.
- In der linearen Algebra heißt eine invertierbare Matrix auch regulär.
- In der Analysis heißt ein Punkt regulär, wenn das Differential an dieser Stelle surjektiv ist. Ein Wert heißt regulär, falls sein Urbild nur aus regulären Punkten besteht.
- In der Funktionentheorie wird regulär manchmal gleichbedeutend mit holomorph gebraucht.
- In der Funktionentheorie bezeichnet man ferner eine hebbare (oder algebraische) Singularität als regulär.
- In der theoretischen Informatik bezeichnet man eine formale Sprache als regulär, wenn sie durch einen regulären Ausdruck, eine reguläre Grammatik oder einen endlichen Automaten erkannt werden kann.
- Eine Bilinearform, die nicht entartet ist, heißt regulär.
- Eine Primzahl p > 2 heißt regulär, wenn sie keine der Bernoulli-Zahlen
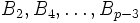 teilt (d.h. wenn die Zähler dieser Zahlen in vollständig gekürzter Darstellung nicht durch p teilbar sind).
teilt (d.h. wenn die Zähler dieser Zahlen in vollständig gekürzter Darstellung nicht durch p teilbar sind).
relativ kompakt
- Eine Menge
![F\subseteq\mathcal{C}([a,b],\mathbb{R})](/pictures/dewiki/55/7fc6e766bdedb87a71c98770b3b8653c.png) heißt relativ kompakt (oder präkompakt), wenn jede Folge aus F eine in
heißt relativ kompakt (oder präkompakt), wenn jede Folge aus F eine in ![\mathcal{C}([a,b],\mathbb{R})](/pictures/dewiki/101/ea799115d6c13f55608e8a3566385c6c.png) konvergente Teilfolge besitzt. Dies ist äquivalent zu: jede Folge aus F besitzt eine in F gleichmäßig konvergente Teilfolge.
konvergente Teilfolge besitzt. Dies ist äquivalent zu: jede Folge aus F besitzt eine in F gleichmäßig konvergente Teilfolge. - eine Teilmenge eines topologischen Raums heißt relativ kompakt, wenn ihr Abschluss kompakt ist.
S
schlicht
- Eine Abbildung
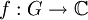 heißt schlicht (auf G) falls f injektiv und f holomorph ist.
heißt schlicht (auf G) falls f injektiv und f holomorph ist.
selbstadjungiert
- Eine Matrix heißt selbstadjungiert genau dann, wenn sie hermitesch ist. Siehe hermitesch.
- In der Funktionalanalysis heißt ein linearer Operator f auf einem Hilbert-Raum H selbstadjungiert, wenn das innere Produkt (,) für alle x und y aus H die Beziehung (x,fy)=(fx,y) erfüllt und f auf ganz H definiert ist.
Ein selbstadjungierter Operator heißt auch hermitesch oder symmetrisch.
Ist f nicht auf ganz H definiert, sondern nur auf einem Teilraum D(f) von H, so sind die Begriffe symmetrisch und selbstadjungiert im Allgemeinen verschieden. Jeder selbstadjungierte Operator f ist symmetrisch, aber nicht jeder symmetrische Operator ist selbstadjungiert.
seltsam
semidefinit
- Eigenschaft von Bilinearformen, siehe Definitheit
semilinear
- Eine Abbildung f: V→W zwischen zwei Vektorräumen über dem Körper C der komplexen Zahlen heißt semilinear (oder auch antilinear), wenn f(v + w) = f(v) + f(w) und
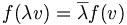 mit v, w aus V und λ aus C. Der Strich über dem Koeffizienten λ bezeichnet komplexe Konjugation.
mit v, w aus V und λ aus C. Der Strich über dem Koeffizienten λ bezeichnet komplexe Konjugation. - Ist allgemeiner R ein Ring und
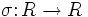 ein Endomorphismus, so heißt eine additive Abbildung
ein Endomorphismus, so heißt eine additive Abbildung 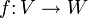 σ-semilinear, wenn
σ-semilinear, wenn 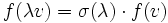 für alle
für alle 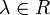 und
und 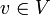 gilt.
gilt.
separabel
- Ein topologischer Raum ist separabel, falls er eine abzählbare dichte Teilmenge hat. Beispiel: Die Menge
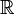 ist separabel, weil
ist separabel, weil 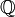 dicht in
dicht in  liegt.
liegt. - Ein Polynom über einem Körper ist separabel, wenn (es gibt zwei Definitionen):
- es in seinem Zerfällungskörper nur einfache Nullstellen hat, bzw.
- jeder seiner irreduziblen Teiler in seinem Zerfällungskörper nur einfache Nullstellen hat.
- Siehe Körpererweiterung.
sesquilinear
- Eine Abbildung
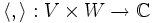 (mit zwei Vektorräumen V, W und dem Körper
(mit zwei Vektorräumen V, W und dem Körper  der komplexen Zahlen) heißt sesquilinear (anderthalbfach linear), wenn sie linear im einen und semilinear im anderen Argument ist, wenn also
der komplexen Zahlen) heißt sesquilinear (anderthalbfach linear), wenn sie linear im einen und semilinear im anderen Argument ist, wenn also 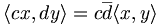 oder, in der entgegengesetzten, ebenfalls gebräuchlichen Konvention,
oder, in der entgegengesetzten, ebenfalls gebräuchlichen Konvention, 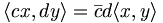 . Das innere Produkt in einem unitären Raum ist eine hermitesche Form, also eine Sesquilinearform
. Das innere Produkt in einem unitären Raum ist eine hermitesche Form, also eine Sesquilinearform 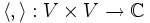 , die unter Vertauschung der beiden Argumente in ihr komplex Konjugiertes übergeht.
, die unter Vertauschung der beiden Argumente in ihr komplex Konjugiertes übergeht.
singulär
- Eine quadratische Matrix heißt singulär, wenn sie nicht invertierbar ist.
- In der Analysis heißt ein Punkt singulär (oder kritisch), wenn das Differential an dieser Stelle nicht surjektiv ist. Ein Wert heißt singulär, falls sein Urbild einen singulären Punkt enthält.
speziell
- Die spezielle lineare Gruppe SL(V), die spezielle orthogonale Gruppe SO(V), die spezielle unitäre Gruppe SU(V) entstehen aus der allgemeinen linearen Gruppe GL(V), der orthogonalenGruppe O(V) und der unitären Gruppe U(V) durch Beschränkung auf Matrizen mit der Determinante 1.
stark wohlgeordnet
- Eine wohlgeordnte Klasse, deren Anfangsstrecken Mengen sind, heißt stark wohlgeordnet.
stationär
- Eine Folge (Mathematik)
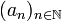 heißt stationär, falls ein m existiert sodass für alle
heißt stationär, falls ein m existiert sodass für alle 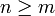 gilt: an = am
gilt: an = am - Ein stochastischer Prozess heißt stationär, wenn dessen partielle Ableitung nach einiger Zeit verschwindet, siehe Stationarität.
stetig
- Eine Funktion von einem topologischen Raum in einen anderen heißt stetig, wenn das Urbild jeder offenen Menge offen ist.
- Eine von-Neumann-Algebra vom Typ II wird stetig genannt.
strikt
- Eine Relation „<“ heißt strikte Halbordnung, wenn sie transitiv und irreflexiv ist, wenn es also kein Element x gibt, für das x<x.
surjektiv
- Eine Funktion heißt surjektiv, wenn jedes Element der Wertemenge Funktionswert mindestens eines Elements der Definitionsmenge ist. Wenn man in dieser Definition mindestens durch genau ersetzt, erhält man die Definition von bijektiv. Eine surjektive Funktion heißt gelegentlich Surjektion, in bestimmtem Kontext auch Projektion. Ein surjektiver Homomorphismus von M nach N heißt auch Homomorphismus „von M auf N“.
supplementär
- Zwei Winkel heißen supplementär oder Ergänzungswinkel, wenn sie sich zu einem Winkel von 180° ergänzen
symmetrisch
- Eine Relation R heißt symmetrisch, wenn aus a R b stets b R a folgt.
- Eine Matrix heißt symmetrisch, wenn sie bei Austausch der Indizes (gleichbedeutend mit Spiegelung an der Hauptdiagonalen) in sich selbst übergeht, wenn also für ihre Koeffizienten gilt aij=aji. Eine symmetrische Matrix stimmt mit ihrer Transponierten überein. Viele Symmetrieeigenschaften reeller symmetrischer Matrizen gelten im Fall komplexer Koeffizienten nicht für symmetrische, sondern für hermitesche Matrizen.
- Die symmetrische Gruppe Symn oder Sn besteht aus allen Permutationen einer Menge mit n Elementen, Gruppenoperation ist die Verkettung der Permutationen.
- Eine Funktion
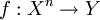 heißt symmetrisch, wenn für alle Permutationen
heißt symmetrisch, wenn für alle Permutationen 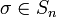 und alle
und alle 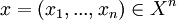 gilt f(x) = f(xσ(1),...,xσ(n)).
gilt f(x) = f(xσ(1),...,xσ(n)).
T
teilbar
- Ein Element a eines Integritätsrings R heißt teilbar durch ein Element b, wenn es ein Element c gibt, sodass die Gleichung a = b · c gilt. b und c heißen dann Teiler von a.
teilgeordnet
total
- Eine Relation R heißt total oder linear, wenn je zwei Elemente in der Relation zueinander stehen, wenn also für jedes Paar von Elementen a, b gilt: a R b oder b R a. Ein Spezialfall davon ist der folgende Punkt:
- Eine strenge Halbordnung „<“ heißt total oder linear, wenn für jedes Paar verschiedener Elemente a, b gilt: a< b oder b < a.
total beschränkt
- Äquivalente Bezeichnung: präkompakt
- Salopp: Eine Menge heißt präkompakt, wenn sie sich mit endlich vielen epsilon-Kugeln überdecken lässt.
- Exakt: Eine Menge M heißt präkompakt, wenn es zu jedem positiven reellen ε eine natürliche Zahl n gibt, sodass es Punkte m1, … mn gibt, sodass die Vereinigung aller Kugeln mit Radius ε um die Punkte mi gerade M enthält.
transitiv
- Eine Relation R heißt transitiv, wenn aus xRy und yRz folgt, dass xRz.
- In der Gruppentheorie ist eine Operation transitiv, wenn sie nur eine Bahn hat, also jedes Element durch ein geeignetes Gruppenelement auf jedes andere Element abgebildet wird. Die Operation heißt zweifach transitiv, wenn die Gruppe transitiv auf der Menge aller Paare operiert, sie heißt scharf transitiv, wenn jedes Element durch genau ein Gruppenelement auf ein gegebenes anderes Element abgebildet wird. Entsprechend gibt es die Begriffe dreifach transitiv, zweifach scharf transitiv etc.
- Eine Menge X ist transitiv, wenn jedes Element eines Elementes von X auch ein Element von X ist.
- In der Stochastik ist eine Markow-Kette transitiv (auch irreduzibel genannt), wenn man von jedem Zustand zu jedem anderen mit einer positiven Wahrscheinlichkeit gelangen kann; siehe irreduzible Markow-Kette
transponiert
- In der linearen Algebra heißen die Matrizen A = (aij) vom Format m×n und AT = (aji) vom Format n×m zueinander transponiert. Siehe auch adjungierte Matrix.
transzendent
- Eine Funktion heißt transzendent, wenn sie nicht durch eine endliche Anzahl elementarer Rechenoperationen dargestellt werden kann, also nicht algebraisch ist.
- Eine komplexe Zahl heißt transzendent, wenn sie nicht algebraisch, also nicht Nullstelle eines Polynoms mit rationalen Koeffizienten ist, siehe transzendente Zahl.
- Ein Element einer Körpererweiterung heißt transzendent, wenn es nicht algebraisch ist, also nicht Nullstelle eines Polynoms mit Koeffizienten aus dem zu erweiternden Körper, siehe algebraisches Element.
treu
- Eine Darstellung heißt treu, wenn der Darstellungshomomorphismus injektiv ist, wenn also verschiedene Gruppenelemente stets durch verschiedene Transformationen dargestellt werden.
- Ein Funktor heißt treu, wenn die Einschränkungen auf den Morphismenmengen zwischen je zwei Objekten injektiv sind.
trigonalisierbar
- Eine Matrix A heißt trigonalisierbar, wenn sie ähnlich zu einer oberen Dreiecksmatrix ist, also wenn es eine invertierbare Matrix S gibt, sodass S − 1AS eine obere Dreiecksmatrix ist. Das ist genau dann der Fall, wenn das charakteristische Polynom in Linearfaktoren zerfällt, was insbesondere über algebraisch abgeschlossenen Körpern, wie den komplexen Zahlen, passiert.
trivial
- Eine mathematische Aussage heißt trivial, wenn sie sich ohne jeden Zwischenschritt aus einer Definition oder einem Satz ergibt. Missbräuchlich wird dieses Attribut auch auf Aussagen angewandt, die auf einem gegebenen Niveau mit vergleichsweise elementaren Mitteln hergeleitet werden können (trivial ist, was der Prof nicht noch einmal erklären möchte).
- Mathematische Objekte heißen trivial, wenn sie besonders einfach sind. Beispiel: Die trivialen Teiler einer natürlichen Zahl n sind 1 und n, man kann sie angeben, ohne genaueres über n (beispielsweise die Primfaktorzerlegung) zu kennen.
- Funktionen und Funktionale heißen trivial, wenn sie auf die Null abbilden; analog sind triviale Räume je nach Kontext entweder leer oder enthalten nur die Null.
U
umkehrbar eindeutig
- Soviel wie bijektiv.
uniform
unimodular
- Eine quadratische Matrix über dem Integritätsbereich R heißt unimodular, wenn ihre Determinante eine Einheit in R ist (s. Hauptartikel: Reguläre Matrix).
- Unter unimodulare Gruppe versteht man:
- die spezielle lineare Gruppe SL(n,K) für n > 1 (s. Hauptartikel: Allgemeine lineare Gruppe, Spezielle lineare Gruppe) oder
- eine topologische Gruppe deren linksinvarintes Haar-Maß rechtsinvariant ist.
- Eine unimodulare Transformation ist eine lineare Transformation mit ganzen rationalen Koeffizienten und Determinante ±1.
- Eine unimodular beschränkte Funktion ist eine auf dem beschränkten Gebiet G definierte holomorphe Funktion f(z):
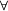 z
z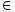 G ( | f(z) |
G ( | f(z) | 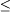 1).
1). - Eine komplexe Zahl z heißt unimodular, wenn | z | = 1.
unitär
- In der abstrakten Algebra heißt ein Ring unitär oder Ring mit 1, wenn er ein bezüglich der Multiplikation neutrales Element besitzt.
- Eine Matrix
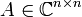 heißt unitär genau dann, wenn
heißt unitär genau dann, wenn 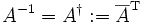 , wenn also ihre Inverse mit ihrer hermitesch Adjungierten übereinstimmt (siehe: Unitäre Matrix).
, wenn also ihre Inverse mit ihrer hermitesch Adjungierten übereinstimmt (siehe: Unitäre Matrix). - Die Menge aller unitären Matrizen vom Rang n über den komplexen Zahlen heißt unitäre Gruppe U(n).
- Ein Innenproduktraum (insbesondere also ein Hilbertraum) heißt unitär, wenn das innere Produkt eine positiv definite hermitesche Form ist. Siehe unitärer Raum.
V
verträglich
verträglich heißt: sowohl linksverträglich als auch rechtsverträglich.
- Sei A eine beliebige Menge,
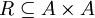 eine Äquivalenzrelation und
eine Äquivalenzrelation und  eine zweistellige innere Verknüpfung auf A. R heißt mit
eine zweistellige innere Verknüpfung auf A. R heißt mit  linksverträglich (bzw. rechtsverträglich), falls für alle
linksverträglich (bzw. rechtsverträglich), falls für alle 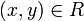 und alle
und alle 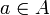 auch
auch 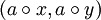 (bzw.
(bzw. 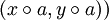 in R liegen. R heißt mit
in R liegen. R heißt mit  verträglich, falls R mit
verträglich, falls R mit  sowohl links- als auch rechtsverträglich ist.
sowohl links- als auch rechtsverträglich ist. - In analoger Weise kann Verträglichkeit auch für n-stellige Relationen und für Abbildungen definiert werden. Ein Distributivgesetz bringt die Verträglichkeit einer Multiplikation mit einer Addition zum Ausdruck.
voll
- Ein Funktor heißt voll, wenn die Einschränkungen auf die Morphismenmengen zwischen je zwei Objekten surjektiv sind.
vollkommen
- Eine natürliche Zahl heißt vollkommen (auch perfekt oder ideal), wenn sie die Summe ihrer echten Teiler (das heißt aller Teiler außer sich selbst) ist. Beispiele: 6=1+2+3, 28 = 1+2+4+7+14. Siehe vollkommene Zahl. Vergleiche auch die Attribute abundant und defizient in diesem Glossar.
vollständig
- Ein formaler Kalkül heißt vollständig, wenn … [?] siehe Vollständigkeit (Logik).
- In der Maßtheorie heißt ein Maß auf einem Maßraum vollständig, wenn jede Teilmenge jeder Nullmenge messbar, also Teilmenge der dem Maß zugrunde liegenden σ-Algebra ist. Mitunter wird der Begriff der Vollständigkeit auch der σ-Algebra zugesprochen, siehe vollständiges Maß.
- Ein metrischer Raum heißt vollständig, wenn jede Cauchy-Folge in ihm konvergiert. Beispiel: ein Hilbertraum ist als ein vollständiger Innenproduktraum definiert. Siehe vollständiger Raum.
- In der Funktionalanalysis gibt es zwei übliche Definitionen von vollständig, die aber inhaltlich nahe beieinander liegen:
- Eine Untermenge S eines topologischen Vektorraums V heißt vollständig, wenn ihre lineare Hülle, d. h. die Menge aller ihrer Linearkombinationen, dicht in V liegt. Manchmal wird eine solche Menge auch als abgeschlossen oder als Grundmenge von V bezeichnet. Ist V separabel, dann kann jeder Vektor aus V durch eine (möglicherweise unendliche) Linearkombination von Vektoren aus S dargestellt werden.
- Im Kontext von Orthonormalsystemen wird vollständig oft auch im Sinne von maximal benutzt: Ein Orthonormalsystem S eines Hilbertraums H heißt vollständig, wenn es in H außer dem Nullvektor keinen Vektor gibt, der zu allen Vektoren aus S orthogonal ist. Im Fall eines separablen Hilbertraums ist eine Orthonormalbasis ein vollständiges Orthonormalsystem – die durch beide Definitionen ausgedrückten Tatsachen sind in diesen Räumen gleichwertig. Eine wichtige Anwendung ist die verallgemeinerte Fouriertransformation.
- Ein Verband heißt vollständig, wenn für jede Teilmenge Supremum und Infimum existieren.
- In der Kategorientheorie heißt eine Kategorie (endlich) vollständig, wenn sie (endliche) Limites enthält.
vorgängerklein
- Eine Relation R heißt vorgängerklein (oder mengenartig, auf engl.: left-narrow bzw. set-like), wenn für jedes y die Klasse {x | xRy} eine Menge ist.
W
wohlgeordnet
- Eine linear geordnete Menge (Klasse) (K, < ) heißt wohlgeordnet, wenn jede Teilmenge (Teilklasse) von K bezüglich der Relation < ein kleinstes Element besitzt (s. Hauptartikel: Wohlordnung).
X
Y
Z
zentral
- zum Zentrum gehörig (z.B. bei Gruppen, Algebren, Liealgebren, von-Neumann-Algebren, ...)
zusammengehörig
Zwei Klassen ohne Maximum, die Unterklassen einer geordenten Klasse sind, heißen zusammengehörig, wenn für jedes Element einer dieser Klassen ein größeres Element aus der anderen Klasse existiert und umgekehrt.
zusammenhängend
- Ein topologischer Raum heißt zusammenhängend, falls es keine disjunkte Zerlegung des Raumes in zwei offene Mengen gibt.
- Siehe auch einfach zusammenhängend als Eigenschaft einer offenen Menge.
zyklisch
- Eine zyklische Gruppe ist eine von einem Element erzeugte Gruppe.
- Eine zyklische Körpererweiterung ist eine Galoiserweiterung, deren Galoisgruppe zyklisch ist.
- Eine Hilbertraum-Darstellung heißt zyklisch, wenn es einen Vektor des Darstellungsraums gibt, so dass der davon erzeugte invariante Unterraum dicht liegt (topologische Variante) bzw. mit dem Darstellungsraum übereinstimmt (algebraische Variante).
zyklotomisch
Das Wort zyklotomisch wurde aus dem englischen cyclotomic oder französischen cyclotomique übernommen und hat sich in einigen Zusammensetzungen als Synonym zum traditionellen deutschen Wortteil „Kreisteilung-“ etabliert.
- Ein zyklotomischer Körper ist ein Kreisteilungskörper, d. h. eine Erweiterung der rationalen Zahlen, die durch Adjunktion von Einheitswurzeln entsteht.
- Ein cyclotomic polynomial oder polynôme cyclotomique ist im Deutschen ein Kreisteilungspolynom. Die Verwendung von „zyklotomisch“ ist in diesem Zusammenhang unüblich.
- Ist G die absolute Galoisgruppe von
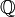 , so definiert die Operation auf den Einheitswurzeln den zyklotomischen Charakter
, so definiert die Operation auf den Einheitswurzeln den zyklotomischen Charakter 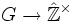 . Die Bezeichnung Kreisteilungscharakter ist weniger gebräuchlich.
. Die Bezeichnung Kreisteilungscharakter ist weniger gebräuchlich.
Einzelnachweise
Wikimedia Foundation.

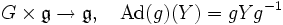
![\mathfrak g\times\mathfrak g\to\mathfrak g,\quad\mathrm{ad}(X)(Y)=[X,Y].](/pictures/dewiki/100/da2a923938f0c2c69d431d8f0b5d5e72.png)