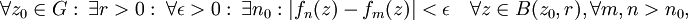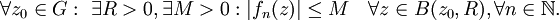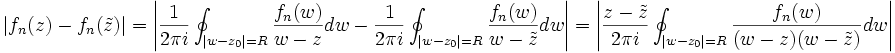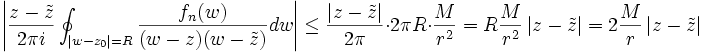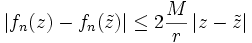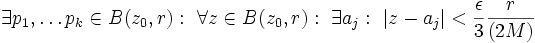- Auswahlsatz von Montel
-
Der Satz von Montel (nach Paul Montel) ist ein Satz aus der Funktionentheorie. Er beschäftigt sich mit der Fragestellung, wann eine Funktionenfolge holomorpher Funktionen eine kompakt konvergente Teilfolge besitzt. In diesem Sinne ist er das Analogon zum Satz von Bolzano-Weierstraß für Zahlenfolgen.
Inhaltsverzeichnis
Der Satz
 sei eine Funktionenfolge, die auf dem Gebiet G holomorph und lokal gleichmäßig beschränkt ist.
sei eine Funktionenfolge, die auf dem Gebiet G holomorph und lokal gleichmäßig beschränkt ist.Dann existiert eine kompakt konvergente Teilfolge
 .
.(Dabei heißt die Folge lokal gleichmäßig beschränkt, wenn sie auf jeder kompakten Menge K gleichmäßig beschränkt ist, d.h.
 .)
.)Beweis
Für den Beweis des Satzes von Montel benötigt man zunächst folgendes Lemma:
Lemma
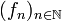 sei eine auf einem Gebiet G holomorphe und lokal gleichmäßig beschränkte Funktionenfolge. Die Menge
sei eine auf einem Gebiet G holomorphe und lokal gleichmäßig beschränkte Funktionenfolge. Die Menge 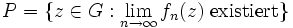 liege dicht in G.
liege dicht in G.Dann ist
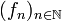 kompakt konvergent.
kompakt konvergent.Beweis (Lemma)
Wir wollen zeigen:
wobei B(z0,r) die offene Kreisscheibe mit Mittelpunkt z0 und Radius r bezeichnet.
Da die Funktionenfolge lokal gleichmäßig beschränkt ist, gilt:
Wähle
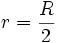 .
.Seien nun
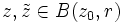 . Dann gilt (Cauchysche Integralformel):
. Dann gilt (Cauchysche Integralformel):Nun schätzt man das Integral durch die Länge der Kurve und das Maximum des Integranden ab (genaugenommen einer Abschätzung des Maximums):
Also gilt:
Nun liegt P dicht in G. Man kann also für jedes vorgegebene ε endlich viele pi aus P wählen, sodass die ε Umgebungen ganz B(z0,r) überdecken. (Da B(z0,r) kompakt ist, reichen endlich viele.) Hier wählen wir unser ε genau so, dass wir dann in Kombination mit der oberen Abschätzung genau ε / 3 erhalten.
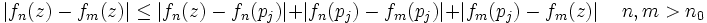
pj sei das zu z nächst gelegene pi. Dann kann man mittels der oberen zwei Abschätzungen den ersten und letzten Summanden jeweils mit ε / 3 abschätzen. Da die fn ja auf den aj punktweise konvergieren, ist auch der mittlere Term (für hinreichend großes n) kleiner als ε / 3.
So erhalten wir:
Beweis (Satz von Montel)
Um das obere Lemma verwenden zu können, wählen wir zunächst eine abzählbare dichte Teilmenge
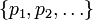 des Gebietes G. (z. B.: Nur jene
des Gebietes G. (z. B.: Nur jene 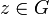 mit rationalen Real- und Imaginärteil)
mit rationalen Real- und Imaginärteil)Nun betrachten wir die Folge
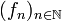 an der Stelle p1. Da die Folge lokal gleichmäßig beschränkt ist, folgt mit dem Satz von Bolzano-Weierstraß, dass eine Teilfolge
an der Stelle p1. Da die Folge lokal gleichmäßig beschränkt ist, folgt mit dem Satz von Bolzano-Weierstraß, dass eine Teilfolge 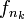 existiert, sodass
existiert, sodass 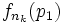 konvergiert. Wir bezeichnen diese Folge mit
konvergiert. Wir bezeichnen diese Folge mit  .
.Nun kann man diese Funktionenfolge im Punkt p2 betrachten. Mit dem gleichen Argument wie oben erhält man, dass es eine im Punkt p2 konvergente Teilfolge
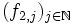 gibt.
gibt.So definiert man induktiv die Funktionenfolgen
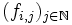 .
.Nun betrachtet man die Diagonalfolge
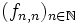 . Diese konvergiert für alle
. Diese konvergiert für alle 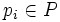 nach dem Cantor'schem Diagonalfolge-Verfahren und ist daher nach dem Lemma auch kompakt konvergent auf dem Gebiet G.
nach dem Cantor'schem Diagonalfolge-Verfahren und ist daher nach dem Lemma auch kompakt konvergent auf dem Gebiet G.Literatur
- E. Freitag, R. Busam: Funktionentheorie 1. Springer-Verlag, ISBN 3-540-31764-3.
Siehe auch
Wikimedia Foundation.