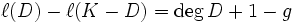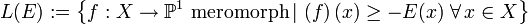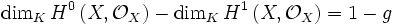Riemann-Roch-Theorem

Der Satz von Riemann-Roch (nach dem Mathematiker Bernhard Riemann und seinem Schüler Gustav Roch) ist eine zentrale Aussage der Theorie kompakter riemannscher Flächen. Er gibt an, wie viele linear unabhängige meromorphe Funktionen mit vorgegebenen Null- und Polstellen auf einer kompakten riemannschen Fläche existieren. Der Satz wurde später auf algebraische Kurven ausgedehnt, noch weiter verallgemeinert und wird auch in der aktuellen Forschung noch weiterentwickelt.

Definition: Divisor

Um Null- und Polstellen einer Funktion an bestimmten Stellen vorschreiben zu können, wird der Begriff Divisor eingeführt. Sei X eine riemannsche Fläche. Eine Funktion 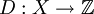$D: X \rightarrow \mathbb{Z}$ heißt Divisor, falls sie nur an isolierten Punkten von null verschieden ist, das heißt, wenn ihre abgeschlossene Trägermenge diskret ist.

Der Divisor einer meromorphen Funktion 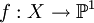$f:X \rightarrow \mathbb{P}^1$ wird mit (f) bezeichnet und ist so definiert, dass jedem Punkt 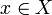$x \in X$ die Null- bzw. Polstellenordnung von f in x zugeordnet wird:

$\left(f\right)(x) := \begin{cases} 0, & f \mbox{ holomorph und ungleich null in } x \\ k, & f \mbox{ hat eine Nullstelle von Ordnung } k \mbox{ in } x \\ -k, & f \mbox{ hat eine Polstelle von Ordnung } k \mbox{ in } x \\ \infty, & f \mbox{ verschwindet in einer Umgebung von } x \end{cases}$

Damit ist der Divisor einer Funktion tatsächlich ein Divisor nach der ersten Definition, wenn die Funktion von der Nullfunktion verschieden ist. Für eine meromorphe 1-Form ω auf X wird der Divisor (ω) wie bei einer Funktion definiert. Ein Divisor D heißt kanonischer Divisor, wenn er sich als Divisor einer meromorphen 1-Form (ω) schreiben lässt, also wenn D = (ω).

Für eine kompakte riemannsche Fläche ist der Grad eines Divisors D definiert durch 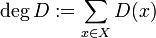$\deg D := \sum_{x \in X} D(x)$. Die Summe ist endlich, da aufgrund der Kompaktheit der Träger aus isolierten Punkten eine endliche Menge sein muss.

Aussage über riemannsche Flächen

Sei X eine kompakte riemannsche Fläche vom topologischen Geschlecht 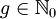$g \in \mathbb{N}_0$ und D ein Divisor auf X. Dann gilt:

$\ell(D) - \ell(K-D) = \deg D + 1 - g$

K steht für einen beliebigen kanonischen Divisor auf X. 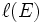$\ell(E)$ bezeichnet für einen Divisor E die Dimension des 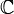$\mathbb{C}$-Vektorraums L(E) der meromorphen Funktionen auf X deren Null- und Polstellen durch den Divisor wie folgt eingeschränkt werden:

$L(E) := \left\{ f : X \rightarrow \mathbb{P}^1 \mbox{ meromorph} \,|\, \left(f\right)(x) \geq -E(x) \; \forall \, x \in X \right\}$

Aussage über algebraische Kurven

Für nicht-singuläre projektive algebraische Kurven X über einem algebraisch abgeschlossenen Körper K wird der Satz von Riemann-Roch üblicherweise mit Hilfe der Kohomologietheorie formuliert.

Er lautet dann:

$\dim_K H^0\left(X, \mathcal{O}_X\right) - \dim_K H^1\left(X, \mathcal{O}_X\right) = 1 - g$

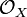$\mathcal{O}_X$ ist die Garbe der regulären Funktionen auf X. Anstelle des topologischen Geschlechts tritt das arithmetische Geschlecht der Kurve, welches im Falle 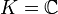$K = \mathbb{C}$ mit dem topologischen zusammenfällt. Der Dualitätssatz von Serre besagt, dass die Formulierung im Falle 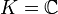$K = \mathbb{C}$ mit derjenigen der des Abschnitts über riemannsche Flächen übereinstimmt.

Konsequenzen

• Als ein erstes Klassifikationsresultat folgt sofort, dass jede riemannsche Fläche vom Geschlecht 0 isomorph ist zur riemannschen Sphäre 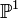$\mathbb{P}^1$, insbesondere kann also auf der Sphäre S² nur eine einzige holomorphe Struktur definiert werden. Für nicht-singuläre projektive Kurven vom Geschlecht 0 gilt entsprechend, dass sie birational äquivalent zu 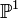$\mathbb{P}^1$ sind.
• Die Formel von Riemann-Hurwitz über das Abbildungsverhalten holomorpher Funktionen zwischen zweien kompakten riemannschen Flächen bzw. über das Abbildungsverhalten von Morphismen zwischen zwei nicht-singulären projektiven Kurven.
• Ein Einbettungssatz: Jede kompakte riemannsche Fläche bzw. jede nicht-singuläre projektive Kurve kann in den projektiven Raum 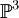$\mathbb{P}^3$ eingebettet werden.

Weitere Verallgemeinerungen

• Satz von Riemann-Roch-Hirzebruch
• Satz von Riemann-Roch-Grothendieck
• Atiyah-Singer-Indexsatz

Literatur

• Otto Forster: Riemannsche Flächen. Springer-Verlag 1977. (vergriffen; engl. Übersetzung lieferbar, ISBN 0-387-90617-7 )
• Klaus Lamotke: Riemannsche Flächen. Springer-Verlag 2005. ISBN 3-540-57053-5
• Robin Hartshorne: Algebraic Geometry. Springer-Verlag 1977. ISBN 0-387-90244-9