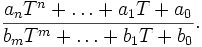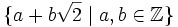- Ringadjunktion
-
Unter Adjunktion versteht man im mathematischen Teilgebiet der Algebra das Hinzufügen von weiteren Elementen zu einem Körper oder Ring.
Inhaltsverzeichnis
Adjunktion algebraischer Elemente zu einem Körper
Es sei K ein Körper und
![f\in K[X]](/pictures/dewiki/99/ccadac4d0b1abd84765b093b0188053b.png) ein irreduzibles Polynom. Dann ist der Faktorring
ein irreduzibles Polynom. Dann ist der Faktorring- L = K[X] / (f)
nach dem von f erzeugten Ideal ein Körper.
Das Polynom f hat in L eine Nullstelle, nämlich das Bild ξ von X. Man sagt deshalb: L entsteht aus K durch Adjunktion einer Nullstelle ξ von f und schreibt K(ξ) = L.
Häufig ist f nur implizit in der Notation enthalten, z. B. ist bei
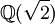 das Polynom f = X2 − 2 gemeint. Normiert man den Leitkoeffizienten von f auf 1, so ist f durch die Bedingung der Irreduzibilität eindeutig bestimmt.
das Polynom f = X2 − 2 gemeint. Normiert man den Leitkoeffizienten von f auf 1, so ist f durch die Bedingung der Irreduzibilität eindeutig bestimmt.Ist der Grad von f gleich n, so lassen sich die Elemente von K(ξ) eindeutig in der Form
 mit
mit 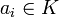 für i = 0,1…,n-1
für i = 0,1…,n-1
schreiben.
Der Grad [K(ξ):K] der Körpererweiterung ist gleich n.
Adjunktion transzendenter Elemente zu einem Körper
Möchte man einen Körper K um ein Element erweitern, das nicht algebraisch sein soll, spricht man von der Adjunktion einer Unbestimmten oder eines transzendenten Elementes T. Der so entstehende Körper K(T) ist definiert als der Quotientenkörper des Polynomringes K[T]. Seine Elemente sind formale rationale Funktionen
Adjunktion bei Ringen
Liegt an Stelle eines Körper allgemeiner ein kommutativer unitärer Ring R vor, so spricht man auch von Erweiterung durch Adjunktion. Die Erweiterungen sind von der Form R[X] / (f) mit einer Unbestimmten X und einem Polynom
![f\in R[X]](/pictures/dewiki/97/abd35e6da207283b3a043689ec2a8e66.png) . Dabei hängt das Verhalten einer derartigen Erweiterung entscheidend davon ab, ob der Leitkoeffizient von f eine Einheit des Ringes ist oder nicht, siehe Ganzheit.
. Dabei hängt das Verhalten einer derartigen Erweiterung entscheidend davon ab, ob der Leitkoeffizient von f eine Einheit des Ringes ist oder nicht, siehe Ganzheit.Beim Übergang von einem Ring R zum Polynomring R[X] spricht man von der Adjunktion einer Unbestimmten.
Beispiele
![\mathbb Z\!\left[\frac12\right]=\mathbb Z[X]/(2X-1)](/pictures/dewiki/51/3adbcc36c7848180674dc285e3308fc4.png) , der Ring der rationalen Zahlen, deren Nenner eine Zweierpotenz ist.
, der Ring der rationalen Zahlen, deren Nenner eine Zweierpotenz ist.![\mathbb Z[\sqrt 2]=\mathbb Z[X]/(X^2-2)](/pictures/dewiki/99/cdd400b301e6a0458cad49c4b0c921f5.png) , der Ring der Elemente von
, der Ring der Elemente von 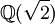 , die die Form
, die die Form
-
- haben.
![\mathbb Z[X]/(X^n - 1)](/pictures/dewiki/54/6f3ac1f36515270d849a29b85e0b4a21.png) ; Ringhomomorphismen von diesem Ring in einen Ring R entsprechen den n-ten Einheitswurzeln in R.
; Ringhomomorphismen von diesem Ring in einen Ring R entsprechen den n-ten Einheitswurzeln in R.
Wikimedia Foundation.