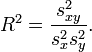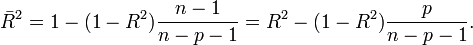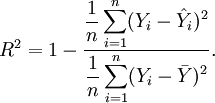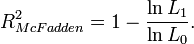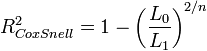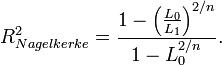- R²
-
Das Bestimmtheitsmaß (abk. R2 oder B, auch Determinationskoeffizient) ist ein Maß der Statistik für den erklärten Anteil der Variabilität (Varianz) einer abhängigen Variablen Y durch ein statistisches Modell. Indirekt wird damit auch der Zusammenhang zwischen der abhängigen und der/den unabhängigen Variablen gemessen (siehe Fehlerreduktionsmaße) [1][2].
Nur im Fall eines linearen Regressionsmodells, d.h. Yi = b0 + b1Xi1 + ... + bpXip + Ui, gibt es eine eindeutige Definition: das Quadrat des multiplen Korrelationskoeffizienten. Ansonsten existieren meist mehrere unterschiedliche Definitionen (siehe Pseudo-Bestimmtheitsmaß).
Inhaltsverzeichnis
Das Bestimmtheitsmaß R2
Interpretation
Die Maßzahl R2 ist der Prozentanteil der Variation von Y (oder auch der Varianz von Y, da gilt Variation(Y) = n * Var(Y)), der durch die lineare Regression erklärt wird, und liegt daher zwischen
- 0 (oder 0 %): kein linearer Zusammenhang und
- 1 (oder 100%): perfekter linearer Zusammenhang.
Ist R2 = 0, dann besteht das "beste" lineare Regressionsmodell nur aus der Konstanten b0, alle anderen Koeffizienten bi sind Null. Ist R2 = 1, dann lässt sich die Variable Y vollständig durch das lineare Regressionsmodell erklären.
Konstruktion
Die Variation von Y wird zerlegt in die Variation der Residuen (durch das Modell nicht erklärte Variation) und die Variation der Regresswerte (durch das Modell erklärte Variation):
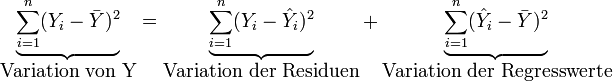
mit
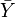 der Mittelwert der Y's,
der Mittelwert der Y's, 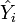 die geschätzten Regresswerte aus dem Regressionsmodell (
die geschätzten Regresswerte aus dem Regressionsmodell (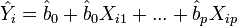 ).
).Damit wird das Bestimmtheitsmaß R2 definiert als:
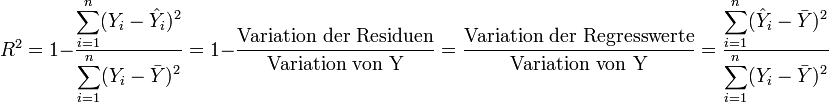
In der Literatur findet man auch folgende Notation für die
- Variation von Y: TSS = SSTotal (total sum of squares),
- Variation der Residuen: RSS = SSResiduen (sum of squared residual) und
- Variation der Regresswerte: ESS = SSRegression (estimated sum of squares).
Zusammenhang mit Korrelationskoeffizienten
Bei einer einfachen Regression (nur eine unabhängige Variable) entspricht R2 dem Quadrat des Pearson'schen Korrelationskoeffizienten R und lässt sich aus der Kovarianz sxy und den Einzelvarianzen
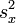 und
und 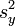 berechnen:
berechnen:Bei einer multiplen Regression (mehr als eine unabhängige Variable) entspricht R2 dem Quadrat des multiplen Korrelationskoeffizienten, also der Korrelation zwischen Y und b1X1 + ... + bpXp.
Grenzen und Kritik
- Das Bestimmtheitsmaß zeigt zwar die Qualität der linearen Approximation, jedoch nicht, ob das Modell richtig spezifiziert wurde. Modelle, die mittels kleinster Quadrate geschätzt wurden, werden daher die höchsten R2 erhalten. Übliche Mißverständnisse sind:
- Ein hohes R2 erlaubt eine gute Vorhersage. Die rote Daten in der Grafik rechts legen nahe, dass sich die Richtung der Daten für höherere Wert von X ändert.
- Ein hohes R2 gibt an, dass die geschätzte Regressionslinie eine gute Approximation an die Daten darstellt; die rote Daten legen auch hier etwas anderes nahe.
- Ein R2 nahe bei Null, zeigt an, dass es keinen Zusammenhang zwischen der abhängigen und den unabhängigen Variablen gibt. Die blauen Daten in der Grafik rechts zeigen einen deutlichen, allerdings nicht-linearen, Zusammenhang, obwohl R2 Null ist.
- Es sagt nichts darüber aus, ob die unabhängigen Variablen Xi wirklich der Grund für die Änderungen in Y sind. Z.B. gibt es tatsächlich einen Zusammenhang zwischen der Anzahl der Störche und der Anzahl der neugeborenen Kinder in einem Gebiet. Der Grund für den Zusammenhang ist jedoch, dass in einem mehr ländlichen Gebiet sowohl die Zahl der Störche als auch die Zahl der neugeborenen Kinder grösser ist als in einem mehr städtisch geprägten Gebiet. Korrekterweise müsste man statt einer Regression Zahl der Kinder = b0 + b1Zahl der Störche eine Regression Zahl der Kinder = b0 + b1Städtische Ausprägung durchführen.
- Außerdem sagt es nichts über die statistische Signifikanz des ermittelten Zusammenhangs und der einzelnen Regressoren aus. Dazu muss zusätzlich ein Signifikanztest durchgeführt werden.
- Es macht keine Aussage über Multikollinearität der unabhängigen Variablen Xi.
- Es macht keine Aussage, ob eine Transformation der Daten die Erklärungskraft der Regression verbessert.
- Ein weiterer Nachteil liegt in der Empfindlichkeit gegenüber Trends: Sofern sich eine exogene Variable parallel zu einer erklärenden entwickelt, werden unabhängig von der wahren Erklärungskraft des Modells hohe R2 ausgewiesen.
Das korrigierte Bestimmtheitsmaß
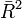
Definition
Das Bestimmtheitsmaß R2 hat die Eigenschaft, dass es umso größer wird je größer die Zahl der unabhängigen Variablen ist. Und zwar unabhängig davon, ob weitere unabhängige Variablen wirklich einen Beitrag zur Erklärungskraft liefern. Daher ist es ratsam, das korrigierte Bestimmtheitsmaß (auch bereinigtes, adjustiertes oder angepasstes Bestimmtheitsmaß genannt) zu Rate zu ziehen. Es berechnet sich wie folgt
Hierbei wird die Erklärungskraft des Modells, repräsentiert durch R2, ausbalanciert mit der Komplexität des Modells, repräsentiert durch p, die Anzahl der unabhängigen Variablen. Je komplexer das Modell ist, desto mehr "bestraft"
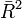 jede neu hinzugenommene unabhängige Variable.
jede neu hinzugenommene unabhängige Variable.Das angepasste Bestimmtheitsmaß
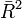 steigt nur, wenn R2 ausreichend steigt, um den gegenläufigen Effekt des Quotienten
steigt nur, wenn R2 ausreichend steigt, um den gegenläufigen Effekt des Quotienten 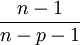 auszugleichen und kann auch sinken. Auf diese Weise lässt sich
auszugleichen und kann auch sinken. Auf diese Weise lässt sich 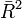 als Entscheidungskriterium bei der Auswahl zwischen zwei alternativen Modellspezifikationen (etwa einem restringierten und einem unrestringierten Modell) verwenden.
als Entscheidungskriterium bei der Auswahl zwischen zwei alternativen Modellspezifikationen (etwa einem restringierten und einem unrestringierten Modell) verwenden.Das korrigierte Bestimmtheitsmaß
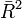 kann auch negative Werte annehmen und ist kleiner als das unbereinigte, außer falls
kann auch negative Werte annehmen und ist kleiner als das unbereinigte, außer falls 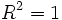 , dann ist auch
, dann ist auch 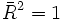 .
.Konstruktion
Aus der obigen Definition von R2 folgt, dass
Wir wissen jedoch, dass
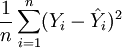 und
und 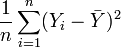 keine unverzerrten Schätzer für die Varianzen sind. Setzt man oben und unten unverzerrte Schätzer ein, so erhält man das korrigierte Bestimmtheitsmaß:
keine unverzerrten Schätzer für die Varianzen sind. Setzt man oben und unten unverzerrte Schätzer ein, so erhält man das korrigierte Bestimmtheitsmaß: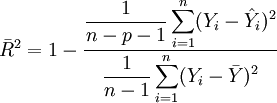 .
.
Pseudo-Bestimmtheitsmaß
Bei einem nominalen oder ordinalen Skalenniveau von Y kann man weder ein lineares Regressionsmodell aufstellen noch eine Variation oder Varianz und damit ein R2 berechnen. Mit Hilfe der Maximum-Likelihood-Schätzung lassen sich jedoch allgemeinere Regressionsmodelle schätzen. In solchen Modellen wird das sogenannte Pseudo-Bestimmtheitsmaß verwendet. Unter diesem Begriff wurden verschiedene Maße vorgeschlagen, darunter das unter Ökonomen am häufigsten verwendete von McFadden[3] (mit lnL0 aus dem Modell mit lediglich einer Konstanten):
Dabei ist L1 der Wert der Likelihoodfunktion unter Kenntnis des Zusammenhanges zwischen Y und Xi (volles Regressionsmodell) und L0 der Wert der Likelihoodfunktion ohne Kenntnis des Zusammenhanges zwischen Y und Xi (Nullmodell ohne Xi). Dieser Ansatz nutzt die Interpretation von R2 als proportionales Fehlerreduktionsmaß aus. Weitere Maße sind die Maße von Cox und Snell[4]
bzw., da gilt
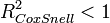 , die Erweiterung von Nagelkerke[5]
, die Erweiterung von Nagelkerke[5]Nagelkerke gab auch eine allgemeine Bedingungen für ein Pseudo-Bestimmtheitsmaß an:
- Ein Pseudo-Bestimmtheitsmaß sollte mit dem Bestimmtheitsmaß R2 übereinstimmen, wenn beide berechnet werden können.
- Es soll ebenfalls maximiert werden mit der Maximum-Likelihood-Schätzung des Modells.
- Es soll, zumindest asymptotisch, unabhängig vom Stichprobenumfang sein.
- Die Interpretation sollte die durch das Modell erklärte Variabilität von Y sein.
- Es soll zwischen Null und Eins liegen. Bei einem Wert von Null sollte es keine Aussage über die Variabilität von Y machen; bei einem Wert von Eins, sollte es die Variabilität von Y mvollständig erklären.
- Es sollte keine Maßeinheit besitzen.
Literatur
- Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W. (1996), Applied linear statistical models (Fourth edition), McGraw-Hill
Einzelnachweise
- ↑ Yule, G.U. (1897), On the theory of correlation, Journal of the Royal Statistical Society, 62, S. 249-295
- ↑ Pearson, K., Lee, A. (1897), On the Distribution of Frequency (Variation and Correlation) of the Barometric Height at Divers Stations, Philosophical Transactions of the Royal Society of London. Series A, Vol. 190, S. 423-469
- ↑ McFadden, D. (1974), Conditional logit analysis of qualitative choice behaviour, in: P. Zarembka (ed.), Frontiers in Econometrics, Academic Press, New York, S. 105-142.
- ↑ Cox, D.R., Snell, E.J. (1989), The Analysis of Binary Data (2. Auflage), Chapman and Hall, London.
- ↑ Nagelkerke, N.J.D. (1991), A Note on a General Definition of the Coefficient of Determination, Biometrika 78(3), S. 691–692.
Wikimedia Foundation.