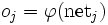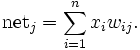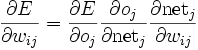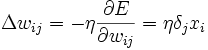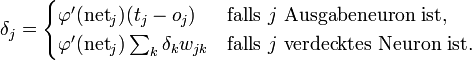Back-Propagation

Backpropagation oder auch Backpropagation of Error bzw. selten auch Fehlerrückführung^[1] (auch Rückpropagierung) ist ein verbreitetes Verfahren für das Einlernen von künstlichen neuronalen Netzen. Formuliert wurde es zuerst 1974 durch Paul Werbos. Bekannt wurde es allerdings erst durch die Arbeit von David E. Rumelhart, Geoffrey E. Hinton und Ronald J. Williams ab 1986 und führte zu einer „Renaissance“ der Erforschung künstlicher neuronaler Netze.

Es gehört zur Gruppe der überwachten Lernverfahren und wird als Verallgemeinerung der Delta-Regel auf mehrschichtige Netze angewandt. Dazu muss ein externer Lehrer existieren, der zu jedem Zeitpunkt der Eingabe die gewünschte Ausgabe, den Zielwert, kennt. Die Rückwärtspropagierung ist ein Spezialfall eines allgemeinen Gradientenverfahren in der Optimierung, basierend auf dem mittleren quadratischen Fehler.

Fehlerminimierung

Beim Lernproblem wird für beliebige Netze eine möglichst genaue Abbildung von gegebenen Eingabevektoren auf gegebene Ausgabevektoren angestrebt. Dazu wird die Qualität der Abbildung durch eine Fehlerfunktion beschrieben, die hier durch den quadratischen Fehler definiert wird:

$E={1\over2} \sum^{n}_{i=1} (t_{i}-o_{i})^{2}$.

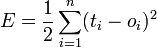Dabei ist

E der Fehler,

n die Anzahl der Muster, die dem Netz vorgestellt werden,

t_i die gewünschte Soll-Ausgabe oder Zielwert (target) und

o_i die errechnete Ist-Ausgabe (output).

Der Faktor 1 / 2 wird dabei lediglich zur Vereinfachung bei der Ableitung hinzugenommen.

Das Ziel ist nun die Minimierung der Fehlerfunktion, wobei aber im Allgemeinen lediglich ein lokales Minimum gefunden wird. Das Einlernen eines künstlichen neuronalen Netzes erfolgt bei dem Backpropagation-Verfahren durch die Änderung der Gewichte, da die Ausgabe des Netzes – außer von der Aktivierungsfunktion – direkt von ihnen abhängig ist.

Algorithmus

Der Backpropagation-Algorithmus läuft in folgenden Phasen:

• Ein Eingabemuster wird angelegt und vorwärts durch das Netz propagiert.
• Die Ausgabe des Netzes wird mit der gewünschten Ausgabe verglichen. Die Differenz der beiden Werte wird als Fehler des Netzes erachtet.
• Der Fehler wird nun wieder über die Ausgabe- zur Eingabeschicht zurück propagiert, dabei werden die Gewichtungen der Neuronenverbindungen abhängig von ihrem Einfluss auf den Fehler geändert. Dies garantiert bei einem erneuten Anlegen der Eingabe eine Annäherung an die gewünschte Ausgabe.

Der Name des Algorithmus ergibt sich aus dem Zurückpropagieren des Fehlers (engl. error back-propagation).

Herleitung

Die Formel des Backpropagation-Verfahrens wird durch Differenziation hergeleitet: Für die Ausgabe eines Neurons abhängig zweier Eingaben x und y erhält man eine zweidimensionale Hyperebene, wobei der Fehler des Neurons abhängig von den Gewichtungen w_x der Eingabe x und w_y der Eingabe y ist. Diese Fehleroberfläche enthält Minima, die es zu finden gilt. Dies kann nun durch das Gradientenverfahren erreicht werden, indem von einem Punkt auf der Oberfläche aus in Richtung des stärksten Abfallens der Fehlerfunktion abgestiegen wird.

Neuronenausgabe

Künstliches Neuron mit Index j

Für die Herleitung des Backpropagation-Verfahrens sei die Neuronenausgabe eines künstlichen Neurons kurz dargestellt. Die Ausgabe o_j eines künstlichen Neurons j lässt sich definieren durch

$o_{j}=\varphi(\mbox{net}_{j})$

und die Netzeingabe net_j durch

$\mbox{net}_{j}=\sum^{n}_{i=1} x_{i} w_{ij}.$

Dabei ist

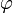$\varphi$ eine differenzierbare Aktivierungsfunktion,

n die Anzahl der Eingaben,

x_i die Eingabe i und

w_ij die Gewichtung zwischen Neuron i und Neuron j.

Auf einen Schwellwert θ_j wird hier verzichtet. Dieser wird meist durch ein immer "feuerndes" ON-Neuron realisiert und das Gewicht zu diesem entsprechend mit dem konstanten Wert 1 belegt. Auf diese Weise entfällt eine Unbekannte.

Ableitung der Fehlerfunktion

Die partielle Ableitung der Fehlerfunktion E ergibt sich durch Verwendung der Kettenregel:

${\partial E \over \partial w_{ij}} = {\partial E \over \partial o_{j}} {\partial o_{j} \over \partial \mbox{net}_{j}} {\partial \mbox{net}_{j} \over \partial w_{ij}}$

Einfaches Netz mit verdeckter Schicht und Ausgabeschicht mit jeweils drei bzw. zwei Neuronen.

Aus den einzelnen Termen kann nun die folgende Formel berechnet werden, dabei ist die Herleitung, im Gegensatz zur einfachen Delta-Regel, abhängig von zwei Fällen:

1. Liegt das Neuron in der Ausgabeschicht, so ist es direkt an der Ausgabe beteiligt,
2. liegt es dagegen in einer verdeckten Schicht, so kann die Anpassung nur indirekt berechnet werden.

$\Delta w_{ij}= -\eta {\partial E \over \partial w_{ij}} = \eta \delta_{j} x_{i}$

mit

$\delta_{j}=\begin{cases} \varphi'(\mbox{net}_{j})(t_{j}-o_{j}) & \mbox{falls } j \mbox{ Ausgabeneuron ist,}\\ \varphi'(\mbox{net}_{j}) \sum_{k} \delta_{k} w_{jk} & \mbox{falls } j \mbox{ verdecktes Neuron ist.} \end{cases}$

Dabei ist

Δw_ij die Änderung des Gewichts w_ij der Verbindung von Neuron i zu Neuron j,

η eine feste Lernrate, mit der die Stärke der Gewichtsänderungen bestimmt werden kann,

δ_j das Fehlersignal des Neurons j,

x_i die Eingabe des Neurons i,

t_j die Soll-Ausgabe des Ausgabeneurons j,

o_j die Ist-Ausgabe des Ausgabeneurons j und

k der Index der nachfolgenden Neuronen von j.

Modifizierung der Gewichte

Die Variable δ_j geht dabei auf die Unterscheidung der Neuronen ein: Liegt das Neuron in einer verdeckten Schicht, so wird seine Gewichtung abhängig von dem Fehler geändert, den die nachfolgenden Neuronen erzeugen, welche wiederum ihre Eingaben aus dem betrachteten Neuron beziehen.

Die Änderung der Gewichte kann nun wie folgt vorgenommen werden:

$w_{ij}^{\mbox{neu}}=w_{ij}^{\mbox{alt}} + \Delta w_{ij}$.

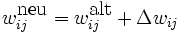Dabei ist

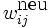$w_{ij}^{\mbox{neu}}$ der neue Wert des Gewichts,

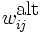$w_{ij}^{\mbox{alt}}$ der alte Wert des Gewichts und

Δw_ij die oben berechnete Änderung des Gewichts.

Erweiterung

Die Wahl der Lernrate η ist wichtig für das Verfahren, da ein zu hoher Wert eine starke Veränderung bewirkt, wobei das Minimum verfehlt werden kann, während eine zu kleine Lernrate das Einlernen unnötig verlangsamt.

Verschiedene Optimierungen von Rückwärtspropagierung, z. B. Quickprop, zielen vor allem auf die Beschleunigung der Fehlerminimierung; andere Verbesserungen versuchen vor allem die Zuverlässigkeit zu erhöhen.

Backpropagation mit variabler Lernrate

Um eine Oszillation des Netzes, d. h. alternierende Verbindungsgewichte zu vermeiden, existieren Verfeinerungen des Verfahrens bei dem mit einer variablen Lernrate η gearbeitet wird.

Backpropagation mit Trägheitsterm

Durch die Verwendung eines variablen Trägheitsterms (Momentum) α kann der Gradient und die letzte Änderung gewichtet werden, so dass die Gewichtsanpassung zusätzlich von der vorausgegangenen Änderung abhängt. Ist das Momentum α gleich 0, so hängt die Änderung allein vom Gradienten ab, bei einem Wert von 1 lediglich von der letzten Änderung.

Ähnlich einer Kugel, die einen Berg hinunter rollt und deren aktuelle Geschwindigkeit nicht nur durch die aktuelle Steigung des Berges, sondern auch durch ihre eigene Trägheit bestimmt wird, lässt sich der Backpropagation ein Trägheitsterm hinzufügen:

Δw_ij(t + 1) = ηδ_jx_i + αΔw_ij(t)

Dabei ist

Δw_ij(t + 1) die Änderung des Gewichts w_ij(t + 1) der Verbindung von Neuron i zu Neuron j zum Zeitpunkt (t+1),

η eine Lernrate,

δ_j das Fehlersignal des Neurons j und

x_i die Eingabe des Neurons i,

α der Einfluss des Trägheitsterms Δw_ij(t). Dieser entspricht der Gewichtsänderung zum vorherigen Zeitpunkt.

Damit hängt die aktuelle Gewichtsänderung (t + 1) sowohl vom aktuellen Gradienten der Fehlerfunktion (Steigung des Berges, 1. Summand), als auch von der Gewichtsänderung des vorherigen Zeitpunktes ab (eigene Trägheit, 2. Summand).

Durch den Trägheitsterm werden unter anderem Probleme der Backpropagation-Regel in steilen Schluchten und flachen Plateaus vermieden. Da z.B. in flachen Plateaus der Gradient der Fehlerfunktion sehr klein wird, käme es ohne Trägheitsterm unmittelbar zu einem "Abbremsen" des Gradientenabstiegs, dieses "Abbremsen" wird durch die Addition des Trägheitsterms verzögert, so dass ein flaches Plateau schneller überwunden werden kann.

Sobald der Fehler des Netzes minimal wird, kann das Einlernen abgeschlossen werden und das mehrschichtige Netz ist nun bereit, die erlernten Muster zu klassifizieren.

Literatur

• David E. Rumelhart, Geoffrey E. Hinton und Ronald J. Williams Learning representations by back-propagating errors., Nature (London) 323, S. 533-536
• Raúl Rojas Theorie der Neuronalen Netze, Springer 1996, ISBN 3540563539 E-Book der englischen Version
• Burkhard Lenze, Einführung in die Mathematik neuronaler Netze. Logos-Verlag, Berlin, 2003, ISBN 3-89722-021-0
• Robert Callan, Neuronale Netze im Klartext, Pearson Studium, München, 2003.
• Andreas Zell, Simulation neuronaler Netze, R. Oldenbourg Verlag, München, 1997, ISBN 3-486-24350-0

Weblinks

• Backpropagator's Review (lange nicht gepflegt)
• Ein kleiner Überblick über Neuronale Netze (D. Kriesel) - Größtes kostenloses Skriptum (knapp 200 Seiten, PDF, 4,6MB) in Deutsch zu Neuronalen Netzen. Sehr reich illustriert und anschaulich. Enthält ein Kapitel über Backpropagation samt Motivation, Herleitung und Variationen wie z.B. Trägheitsterm, Lernratenvariationen u.a.
• Membrain: freier Neuronale-Netze-Editor-und-Simulator für Windows
• Leicht verständliches Tutorial über Backpropagation mit Implementierungen (Englisch)
• Backpropagation in Ruby

Quellen

1. ↑ Werner Kinnebrock: Neuronale Netze: Grundlagen, Anwendungen, Beispiele. R. Oldenbourg Verlag, München 1994, ISBN 3-486-22947-8