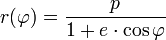- Bahnparameter
-
Die Bahnelemente beschreiben die mittlere Bahn eines Astronomischen Objekts. Die Bewegung wird mit den drei Keplerschen Gesetzen behandelt.
Inhaltsverzeichnis
Die Bahnelemente
Zur Definition einer störungsfreien Keplerbahn sind prinzipiell 6 Bahnelemente erforderlich. Im Zweikörperproblem (ohne Bahnstörungen durch dritte Körper und nicht-gravitative Einflüsse) genügen diese 6 Bahnelemente.
Bahnstörungen verursachen eine langsame Änderung der 6 Bahnelemente, sodass diese nur oskulierende Elemente sind, das heißt, dass sie sich der idealen Bahn nur während eines kurzen Zeitraums anschmiegen. Oft wird daher noch ein siebentes Bahnelement angegeben, einige Störungen können auch durch Angabe zeitlicher Änderungen der Bahnelemente berücksichtigt werden. Prinzipiell wird aber die Oskulationsepoche E angegeben, für die die Daten gelten.
Für Objekte, die starken Störungen unterliegen, werden zusätzliche Elemente angeführt.
Die Gestaltelemente
Zur Beschreibung der Gestalt der Bahnkurve sind zwei Werte erforderlich, die sowohl die Form wie auch die Größe – also als Längenangabe – festlegen. Die Exzentrizität charakterisiert die Form eines Kegelschnitts (Ellipse, Parabel, Hyperbel), die Größe kann entweder mit Hilfe des Parameters oder mit der Periapsisdistanz beschrieben werden. Daneben sind auch andere Angaben möglich:
- Die numerische Exzentrizität e
- (Sie wird in der Mathematik mit ε bezeichnet).
- Der Parameter p
Das sind die grundlegendenden Parameter der allgemeinen Form einer Keplerbahn:
In Spezialfällen werden folgende Werte verwendet, die sich direkt daraus ableiten:
- Die große Halbachse a,α
- Sie ist bei Ellipsenbahnen am zweckmäßigsten. Sie wird im allgemeinen entweder in Kilometer oder in AE angegeben.
- Beispiel Erdbahn: große Halbachse = 149,597 Mio. km = 1 AE
- Die Periapsisdistanz q,rmin
- Entfernung des Hauptscheitels vom Brennpunkt. Typisches Bahnelement eines Kometen, Q bezeichnet dann rmax (auch R), die Apoapsisdistanz periodischer Kometen.
- Der Exzentrizitätswinkel Φ
- Als Alternative zur Exzentrizität
- sinΦ = ε
Die Lageelemente
Zur Beschreibung der Lage im Raum sind ebenfalls zwei Werte erforderlich.
- Die Inklination i
- Das ist der Winkel der Bahnebene zur Referenzebene.
- Das Argument des Knotens (Knotenlänge) Ω
- Der Winkel vom Koordinatennullpunkt der Referenzebene zum aufsteigenden Knoten.
- Beispiel: Die Knotenlänge der Bahn eines Planeten ist die ekliptikale Länge des aufsteigenden Knotens (das ist der Winkel vom Frühlingspunkt zum aufsteigenden Knoten). Die Knotenlänge eines Satelliten ist die Rektaszension (entlang des Erdäquators) bezüglich des Frühlingspunkts.
- Das Argument der Periapsis ω
- Der Winkel vom aufsteigenden Knoten zur Periapsis.
- Im Sonnensystem ist es üblicherweise das Argument des Perihels. Für den Mond oder künstliche Erdsatelliten ist es das Argument des Perigäums.
- Die Länge der Periapsis Π
- als gebrochener Winkel, von denen der erste Summand in der Referenzebene, der zweite in der Bahnebene gemessen wird. Sie ist eine brauchbare Vereinfachung, wenn die Bahnneigung klein ist, zum Beispiel die Perihellänge eines Planeten.
- Π = Ω + ω
- Koordinaten der Periapsis Lπ,Bπ (Winkelelemente)
- Bei der Analyse von Gemeinsamkeiten in den Bahnelementen, insbesondere bei Kometengruppen oder Meteorströmen, benutzt man die Ekliptikalen Winkelkoordinaten der Apsidenlinie bzw. des Periheldurchgangs in Länge und Breite.
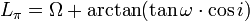
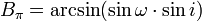
Der Zeitbezug
Auch für den Zeitbezug sind zwei Werte nötig. Man benötigt Werte für den Ort auf der Bahn zum Zeitpunkt oder Bahngeschwindigkeit (Linear oder Winkel):
- Die UmlaufperiodeP
- Für die Umlaufperiode wird entweder die Bahnperiode (anomalistische Umlaufzeit) angegeben oder eine andere Umlaufzeit, etwa für die Planeten des Sonnensystems die siderische Umlaufzeit, bei der Erde das tropische Jahr.
- Die mittlere tägliche Bewegung μ oder n
- Wird für schnell umlaufende Objekte wie nichtstationäre Satelliten benutzt: Die Erdumläufe pro Tag
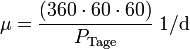
- Die Winkelgeschwindigkeit
- Eine Angabe der beobachtenden Astronomie: So lässt sich die Position aus einer vorhergehenden Beobachtung leicht abschätzen
- Die mittlere Anomalie M
- Für Satelliten und andere Objekte, die starken Bahnstörungen unterliegen – wie dem Mond – wird im allgemeinen die mittlere Anomalie verwendet, das ist die Position eines fiktiven Objekts mit gleichmäßigem Umlauf
- Die mittlere Länge λ,L
- Sie wird gewählt, wenn die Exzentrizität zu klein ist, um mit der Anomalie den Bahnort zu bestimmen; wie die Periapsislänge Π als gebrochener Winkel gezählt.
- L = M + Π
- Die Periapsiszeit T,τ
- Der Zeitpunkt des Periapsisdurchgangs
- Der Radiusvektor R
- Die aktuelle Distanz des Körpers zum Zentralobjekt.
Zusätzliche Elemente
Zur hinreichenden Beschreibung von Bahnstörungen – etwa wenn sich der Körper nicht im hinreichend idealen Vakuum oder einem nahen Mehrkörpersystem bewegt – werden außer den sechs grundlegenden Elementen weitere Bahnelmente angegeben.
- Der Widerstandskoeffizient, als π / 2,B,B *
- Für niedrig-orbitale Raumflugkörper, die noch den Reibungsverlusten durch die Erdatmosphäre unterworfen sind.
Daneben können auch alle oben angegebenen Elemente nicht als Wert, sondern als zeitabhängige Formel gegeben sein, meist als Terme einer oder mehrerer Reihenentwicklungen. So lässt sich der aktuelle Wert mit nötiger Rechengenauigkeit ermitteln.
Übersicht
Bahnelement Verwendbarkeit Bahnelement Bezug Symbol Dimension Ellipse Parabel / Hyperbel Exzentrizität Form e, ε 1 Ja Ja Exzentrizitätswinkel Form Φ 1 Ja Nein Parameter Größe p Länge Ja Ja Periapsis Größe q Länge Ja Ja Große Halbachse Größe a, α Länge Ja Nein Inklination Lage i Winkel Ja Ja Argument des Knotens Lage Ω Winkel Ja teilweise 1 Argument der Periapsis Lage ω Winkel Ja Ja Länge der Periapsis Lage Π Winkel Ja Ja Erste Koordinate der Periapsis Lage Lπ Winkel Ja Ja Zweite Koordinate der Periapsis Lage Bπ Winkel Ja Ja Mittlere Bewegung Zeitverhalten μ, n, V 1 / Zeit Ja Ja Winkelgeschwindigkeit 2 Zeit-Ortverhalten Winkel / Zeit Ja Ja Mittlere Anomalie 2 Bahnort M Winkel Ja Nein Mittlere Länge 2 Bahnort λ, L Winkel Ja Nein Radiusvektor 2 Bahnort R Länge Ja Ja Umlaufperiode Zeitbezug P Zeit Ja Nein Periapsiszeit Zeitbezug T, τ Zeit Ja Ja Die Angabe von Bahnelementen
Die Angabe als 6-Tupel (p, e, i, Ω, ω, T) bezeichnet man als klassische Bahnelemente[1]. Daneben gibt es auch andere Möglichkeiten, die dem jeweiligen Fall angepasst sind, und dann meist kanonisch innerhalb eines Formalismus geregelt ist:
- (a, e, i, Ω, ω, T), eine besonders für Kometen und die Planeten des Sonnensystems geeignete Methode
- (a, e, i, Ω, ω, M), für den Pluto und die Kleinplaneten, wie sie der Astronomical Almanac verwendet[2].
- (a, e, i, Ω, π, L) gibt etwa die Planetentheorie VSOP 82 auf indirektem Wege.
- (i, Ω, e, ω, M, n), das System des NASA/NORAD Two Line Elements Format für künstliche Erdsatelliten
Siehe auch
- Satellitenbahnelement – spezielle Bahnangaben für Erdsatelliten
- Umlaufbahn – die geschlossene Keplerbahn
Literatur
- Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4
- Wolfgang Vollmann: Wandelgestirnörter. In: Hermann Mucke (Hrsg.): Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. Zeiss Planetarium der Stadt Wien und Österreichischer Astronomischer Verein 1992, S. 55–102 (weblink, 6. August 2006)
- Jean Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 1991, ISBN 0-943396-35-2
Weblinks
- Minor Planet Center (englisch)
- Central Bureau for Astronomical Telegrams (englisch)
Einzelnachweise
Wikimedia Foundation.