8-Damenproblem

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Eine Lösung des Acht-Damen-Problems

Das Damenproblem ist eine schachmathematische Aufgabe. Es sollen jeweils acht Damen auf einem Schachbrett so aufgestellt werden, dass keine zwei Damen einander nach den Schachregeln schlagen können. Die Figurenfarbe wird dabei ignoriert und es wird angenommen, dass jede Figur jede andere angreifen könnte. Anders ausgedrückt, es sollen sich keine zwei Damen die gleiche Reihe, Linie oder Diagonale teilen. Im Mittelpunkt steht die Frage nach der Anzahl der möglichen Lösungen.

Das Problem kann auf Schachbretter beliebiger Größe verallgemeinert werden. Dann gilt es, n nicht-dominierende Damen auf einem Brett von n x n Feldern zu positionieren. Für n = 8 hat das Damenproblem 92 verschiedene Lösungen. Betrachtet man Lösungen als gleich, die sich durch Spiegelung oder Drehung des Brettes aus einander ergeben, verbleiben noch zwölf Lösungen.

Geschichte

Erstmals formuliert wurde das Damenproblem von dem bayerischen Schachmeister Max Bezzel. In der Berliner Schachzeitung fragte er 1848 nach der Anzahl der möglichen Lösungen. Als erster nannte 1850 Franz Nauck in der Leipziger Illustrirten Zeitung die korrekte Zahl 92. Auch Carl Friedrich Gauß zeigte Interesse an dem Problem, weshalb es irrtümlich häufig auf ihn zurückgeführt wird. 1874 bewies der englische Mathematiker James Whitbread Lee Glaisher, dass es nicht mehr Lösungen geben kann.^[1] Damit war das ursprüngliche Problem vollständig gelöst.

Nauck verallgemeinerte die Problemstellung und fragte, auf wie viele verschiedene Arten n Damen auf einem n×n-Schachbrett aufgestellt werden können.

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Symmetrische eindeutige Lösung, sorgt für 92 statt 96 verschiedene Lösungen (basierend auf 12 eindeutigen Lösungen)

1991 wurde von B. Bernhardsson eine explizite Lösung des N-Damenproblems für jede beliebige Brettgröße im ACM SIGART Bulletin, Vol. 2, No. 7, angegeben.

Im Jahre 1992 fanden Demirörs, Rafraf und Tanik eine Äquivalenz zwischen magischen Quadraten und Damenproblemen.

Das Damenproblem tauchte auch in The 7th Guest auf, einem Computerspiel aus den 1990er Jahren.

Anzahl der Lösungen im klassischen Damenproblem

Das klassische Problem mit acht Damen auf einem 8x8-Brett hat 92 verschiedene Lösungen. Wenn man solche, die durch Drehen oder Spiegeln des Brettes aufeinander abgebildet werden, nur einfach zählt, bleiben zwölf eindeutige Lösungen übrig (die unterschiedlichen Farben der Felder werden nicht beachtet). Da es für jede dieser reduzierten Lösungen vier Spiegelungen (an Diagonalen, Horizontale und Vertikale durch die Brettmitte) und vier Rotationen gibt, könnte man eine Gesamtzahl von 8·12=96 Lösungen vermuten. Da aber eine der Lösungen (siehe Diagramm) bei einer Drehung um 180° in sich selbst übergeht, lassen sich aus dieser nur vier verschiedene Lösungen konstruieren und es ergeben sich insgesamt 92 Lösungen.

Anzahl der Lösungen im verallgemeinerten Damenproblem

Das verallgemeinerte Damenproblem verlangt, n Damen auf einem Brett von n x n Feldern so zu positionieren, dass sie einander nicht bedrohen.

Anzahl der Lösungen bis zur Brettgröße 25×25

Die folgende Tabelle führt die Anzahl der eindeutigen Lösungen und die der gesamten Lösungen bis zur Brettgröße 25×25 auf:

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
eindeutig	1	0	0	1	2	1	6	12	46	92	341	1.787	9.233	45.752	285.053	1.846.955	11.977.939	83.263.591
insgesamt	1	0	0	2	10	4	40	92	352	724	2.680	14.200	73.712	365.596	2.279.184	14.772.512	95.815.104	666.090.624

n	19	20	21	22	23	24
eindeutig	621.012.754	4.878.666.808	39.333.324.973	336.376.244.042	3.029.242.658.210	28.439.272.956.934
insgesamt	4.968.057.848	39.029.188.884	314.666.222.712	2.691.008.701.644	24.233.937.684.440	227.514.171.973.736

n	25 (Weltrekord – 2005)
eindeutig	275.986.683.743.434
insgesamt	2.207.893.435.808.352

Zur Zeit arbeiten zwei Projekte an der Lösung für n=26:

• Das NQueens@Home^[2]-Projekt nutzt die BOINC-Plattform (siehe Liste der Projekte verteilten Rechnens).
• Das Queens@TUD^[3]-Projekt rechnet auf FPGAs.

Allgemein lässt sich feststellen, dass die Anzahl der Lösungen etwas schneller als exponentiell mit der Brettgröße anwächst. Interessanterweise gibt es auf dem 6×6-Brett weniger Lösungen als auf dem 5×5-Brett.

Anzahl der Lösungen für große n

Eine obere Schranke für die Lösungsanzahl D(n) des Damenproblems auf einem n×n-Brett ist n!. Dies ist die Anzahl von Lösungen für n einander nicht bedrohende Türme. Die Aufstellungen von einander nicht bedrohenden Damen sind eine echte Teilmenge hiervon.

Die asymptotische Form von D(n) ist nicht bekannt. Rivin et al. stellen die Vermutung auf, dass

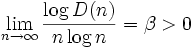$\lim_{n \to \infty} \frac{\log{D(n)}}{n \log{n}}=\beta>0$ ist.^[4]

Aus den bekannten Gliedern der Folge lässt sich weiterhin vermuten, dass für große n gilt:^[5] 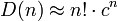$D(n)\approx n! \cdot c^n$ mit $c\approx 0.39$.

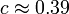Algorithmen zur Lösungssuche

Das Damenproblem ist ein gutes Beispiel für ein einfach zu formulierendes Problem mit nicht-trivialen Lösungen. Eine Reihe von Programmiertechniken ist geeignet, alle Lösungen zu erzeugen. Klassisch ist rekursives Backtracking; dieses ist besonders einfach zu realisieren mit logischer Programmierung. Eine weitere Möglichkeit sind genetische Algorithmen.

Derartige Ansätze sind wesentlich effizienter als ein naiver Brute-Force-Algorithmus, der (im 8×8 Fall) alle 64·63·62·61·60·59·58·57 (knapp 64⁸ = 2⁴⁸) möglichen Positionierungen der acht Damen durchprobiert und dabei alle Stellungen ausfiltert, in denen zwei Damen einander schlagen könnten. Dieser Algorithmus erzeugt mehrfach die gleichen Lösungen, wenn Permutationen der Damen gleiche Felder besetzen.

Ein effizienterer Brute-Force-Algorithmus platziert in jeder Reihe nur eine Dame und reduziert dadurch die Komplexität auf 8⁸ = 2²⁴ mögliche Stellungen.

Rekursives Backtracking

Animation des rekursiven Backtracking-Algorithmus

Das Damenproblem ist ein gutes Beispiel für ein einfaches, aber nicht triviales Problem, das durch einen rekursiven Algorithmus gelöst werden kann, indem das Problem mit n Damen so aufgefasst wird, dass es gilt, zu jeder Lösung mit n-1 Damen eine weitere Dame hinzuzufügen. Letztendlich lässt sich jedes Damenproblem damit auf ein Problem mit 0 Damen zurückführen, was nichts anderes als ein leeres Schachbrett ist.

Das folgende Python-Programm findet alle Lösungen des n-Damenproblems mit Hilfe eines rekursiven Algorithmus. Ein n×n-Brett wird dabei rekursiv auf kleinere Bretter mit geringerer Anzahl an Reihen, n×n-1, n×n-2, … reduziert. Das Programm nutzt direkt aus, dass keine zwei Damen in der gleichen Reihe stehen. Außerdem wird benutzt, dass eine Lösung mit n-1 Damen auf einem n×n-1-Brett auf jeden Fall eine Lösung mit n-2 Damen auf einem n×n-2-Brett enthalten muss. (In anderen Worten, wenn man die untere (oder obere) Reihe der Teillösung eines n×n-1-Bretts entfernt, bleiben n-2 Damen auf einem n×n-2-Brett übrig, die wiederum eine Teillösung auf dem n×n-2-Brett darstellen.)

Der Algorithmus konstruiert also alle Lösungen aus den Lösungen eines jeweils kleineren Brettes. Da sichergestellt wird, dass die Teillösungen auf den kleinen Brettern konfliktfrei sind, spart dieser Algorithmus das Überprüfen vieler Stellungen. Insgesamt werden für das 8×8-Brett nur 15.720 Stellungen überprüft.

# Erzeuge eine Liste von Lösung auf einem Brett mit Reihen und Spalten.
# Eine Lösung wird durch eine Liste der Spaltenpositionen,
# indiziert durch die Reihennummer, angegeben.
# Die Indizes beginnen mit Null.
def damenproblem(reihen, spalten):
    if reihen <= 0:
        return [[]] # Problem nicht definiert, eine Dame auf dem nicht-existierenden Brett
    else:
        return eine_dame_dazu(reihen - 1, spalten, damenproblem(reihen - 1, spalten))
 
# Probiere alle Spalten, in denen für eine gegebene Teillösung
# eine Dame in "neue_reihe" gestellt werden kann.
# Wenn kein Konflikt mit der Teillösung auftritt,
# ist eine neue Lösung des um eine Reihe erweiterten
# Bretts gefunden.
def eine_dame_dazu(neue_reihe, spalten, vorherige_loesungen):
    neue_loesungen = []
    for loesung in vorherige_loesungen:
        # Versuche, eine Dame in jeder Spalte von neue_reihe einzufügen.
        for neue_spalte in range(spalten):
            # print('Versuch: %s in Reihe %s' % (neue_spalte, neue_reihe))
            if kein_konflikt(neue_reihe, neue_spalte, loesung):
                # Kein Konflikte, also ist dieser Versuch eine Lösung.
                neue_loesungen.append(loesung + [neue_spalte])
    return neue_loesungen
 
# Kann eine Dame an die Position "neue_spalte"/"neue_reihe" gestellt werden,
# ohne dass sie eine der schon stehenden Damen schlagen kann?
def kein_konflikt(neue_reihe, neue_spalte, loesung):
    # Stelle sicher, dass die neue Dame mit keiner der existierenden
    # Damen auf einer Spalte oder Diagonalen steht.
    for reihe in range(neue_reihe):
        if loesung[reihe]         == neue_spalte              or  # Gleiche Spalte
           loesung[reihe] + reihe == neue_spalte + neue_reihe or  # Gleiche Diagonale
           loesung[reihe] - reihe == neue_spalte - neue_reihe:    # Gleiche Diagonale
                return False
    return True
 
for loesung in damenproblem(8, 8):
    print(loesung)

Dieser rekursiv programmierte Algorithmus kann leicht in einen nicht-rekursiven (iterativen) umgewandelt werden.

Constraintprogrammierung

Die Constraintprogrammierung über endliche Bereiche kann eine Aufgabe wie das Damenproblem sehr kompakt formulieren. Das folgende Prolog-Programm (in GNU Prolog) findet schnell eine Lösung auch für große Schachbretter.

/* Dieses Prädikat erzeugt eine Liste, die eine einzige Lösung darstellt.
   Es ist sichergestellt, dass jeder Wert zwischen 1 und N genau einmal auftritt. */

n_damen(N,Ls) :- length(Ls,N),
               fd_domain(Ls,1,N),
               fd_all_different(Ls),
               constraint_damen(Ls),
               fd_labeling(Ls,[variable_method(random)]).
 
/* Dieses Prädikat stellt sicher,
   dass alle Stellungen die Lösungsbedingungen erfuellen */

constraint_damen([]).
constraint_damen([X|Xs]) :- nicht_schlagen(X,Xs,1), constraint_damen(Xs).
 
/* Mit diesem Prädikat wird sichergestellt,
   dass zwei Damen nicht auf einer Diagonalen stehen */

nicht_schlagen(_,[],_).
nicht_schlagen(X,[Y|Xs],N) :- X#\=Y+N, X#\=Y-N, T#=N+1, nicht_schlagen(X,Xs,T).

Explizite Lösung

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Konstruktionsvorschrift für gerade n, die nicht bei Division durch sechs den Rest zwei ergeben, funktioniert also bei acht nicht