- 8-Zeller
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Tesserakt
(8-Zeller)
4-Kubus
SchlegeldiagrammGruppe Reguläre Polytope Familie Hyperkubus Zellen 8 (4.4.4) 
Flächen 24 {4} Kanten 32 Ecken 16 Schläfli-Symbole {4,3,3}
{4,3}x{}
{4}x{4}
{4}x{}x{}
{}x{}x{}x{}Coxeter-Dynkin-Diagramme 


































Symmetriegruppe B4, [3,3,4] Eigenschaften konvex Der Tesserakt ist die Verallgemeinerung des klassischen Würfels auf vier Dimensionen. Man spricht dabei auch von einem vierdimensionalen Hyperwürfel. Der Tesserakt verhält sich zum Würfel, wie sich der Würfel zum Quadrat verhält. Er hat 16 Ecken, 32 Kanten, 24 Quadrate, und wird durch 8 würfelförmige Zellen begrenzt.
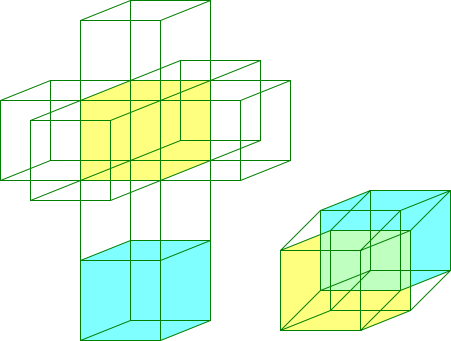
Ein exaktes Modell des Tesserakts ist innerhalb des dreidimensionalen Raumes nicht darstellbar. Daher sind die folgenden Bilder nur als Parallelprojektionen zu verstehen. Unten im ersten Bild erkennt man einen blauen und einen gelben Würfel, die durch sechs weitere rhomboedrisch verzerrte Begrenzungswürfel verbunden sind. Beim dreidimensionalen Netz des Tesserakts (links im ersten Bild) sind alle acht Begrenzungswürfel in den dreidimensionalen Raum gefaltet.
Im folgenden Bild ist das Netz des Tesserakts links zu sehen, und rechts unten die Parallelprojektion des Tesserakts.



Wenn man beim Tesserakt dessen acht gegenüber liegende Begrenzungs-Würfel paarweise mit einander verheftet, dann entsteht ein 4-Torus.
Inhaltsverzeichnis
Entfalten des Tesserakts
Der Tesserakt kann in acht Würfel entfaltet werden, so wie ein Würfel in sechs Quadrate entfaltet werden kann. Es gibt 261 verschiedene Arten, einen Tesserakt zu entfalten.
Projektionen in 2 Dimensionen
Die Konstruktion eines Hyperwürfels kann man sich folgendermaßen vorstellen:
- 1-dimensional: Zwei Punkte A und B können zu einer Linie verbunden werden, es entsteht eine neue Linie AB.
- 2-dimensional: Zwei Parallele Linien AB und CD können zu einem Quadrat verbunden werden, mit den Ecken ABCD.
- 3-dimensional: Zwei parallele Quadrate ABCD und EFGH können zu einem Würfel verbunden werden, mit den Ecken ABCDEFGH.
- 4-dimensional: Zwei parallele Würfel ABCDEFGH und IJKLMNOP können zu einem Hyperwürfel verbunden werden, mit den Ecken ABCDEFGHIJKLMNOP.
Das ist zwar schwer vorstellbar, aber es ist möglich Tesserakte in drei- oder zweidimensionale Räume zu projizieren. Außerdem werden Projektionen in die zweite Dimension aufschlussreicher, wenn man die projizierten Eckpunkte umordnet. In dieser Methode kann man Bilder erhalten, die nicht mehr die Raumbeziehungen innerhalb des Tesserakts widerspiegeln, aber die Verbindungsstruktur der Eckpunkte, wie folgende Beispiele zeigen:
Ein Tesserakt wird im Prinzip durch zwei verbundene Würfel gebildet. Das Schema ist der Konstruktion eines Würfels von zwei Quadraten ähnlich: Stellen Sie zwei Kopien des niedrigerdimensionalen Würfels nebeneinander und verbinden Sie die entsprechenden Scheitelpunkte. Jede Kante eines Tesserakts ist von derselben Länge. Acht Würfel, die miteinander verbunden sind.
Tesserakte sind auch zweiteilige Graphen, genau wie Linien, Quadrate, Würfel und Bäume.
Projektionen in 3 Dimensionen
 Das Rhombendodekaeder bildet die Hülle dieser Projektion eines Tesserakts in 3 Dimensionen
Das Rhombendodekaeder bildet die Hülle dieser Projektion eines Tesserakts in 3 DimensionenDie Zelle-Zuerst-Parallelprojektion des Tesserakts in den 3-dimensionalen Raum hat eine würfelförmige Hülle. Die nächsten und entferntesten Flächen werden auf den Würfel projiziert und die übrigen 6 Zellen werden auf die quadratischen Flächen des Würfels projiziert.
Die Fläche-Zuerst-Parallelprojektion des Tesserakts in den 3-dimensionalen Raum hat eine quaderförmige Hülle. Zwei Paare der projizieren die obere und untere Hälfte der Hülle und die 4 übrigen Zellen werden auf die Seitenflächen projiziert.
Die Kante-Zuerst-Parallelprojektion des Tesserakts in den 3-dimensionalen Raum hat eine Hülle in der Form eines hexagonalen Prismas. Sechs Zellen werden auf rhombische Prismen projiziert, die im hexagonalen Prisma ausgelegt sind analogdazu wie die Flächen eines 3D-Würfels auf eine hexagonale Hülle in der Ecke-Zuerst-Projektion ausgelegt sind. Die zwei übrigen Zellen sind auf die Basen des Prismas projiziert.
Die Ecke-Zuerst-Parallelprojektion des Tesserakts in den 3-dimensionalen Raum hat eine rhombische dodekaederförmige Hülle.Bildergalerie

Stereografische Projektion
(Die Kanten sind auf eine Hyperkugel projiziert)
Einfache Ecken-Grafik
Eine 3D-Projektion eines 8-Zellers, der eine einfache Rotation um eine Ebene, die die Figur von vorne links nach hinten rechts und von oben nach unten teilt, ausführt.
Eine 3D-Projektion eines 8-Zellers, der eine doppelte Rotation um zwei orthogonale Ebenen ausführt.Orthogonale Projektion 



Ein Netz eines Tesserakts.
(Animation ansehen.)
Eine stereografische 3D-Projektion eines Tesserakts.Siehe auch
- Im Film Cube 2: Hypercube spielt das Tesserakt eine große Rolle, ebenso in der Fernsehserie Gene Roddenberry's Andromeda. Es existiert ein niederländisches Techno-Label mit dem Namen Tesseract Records. Außerdem existiert eine englische Band namens Tesseract.
Weblinks
- Animation eines Tesserakts
- Darstellung von Schrägbildern, Zentralprojektionen, Netzen und Schnitten eines Tesserakts
- Platonische Polychora
- Crucifixion (Corpus Hypercubus) Gemälde von Salvador Dalí, welches das Netz des Tesserakts enthält.
- Per Java animierter Tesserakt
Wikimedia Foundation.