- Baire'scher Kategoriensatz
-
Der Satz von Baire, auch als bairescher Kategoriensatz bezeichnet, gilt für eine Vielzahl topologischer Räume, die in verschiedenen Teilgebieten der Mathematik, wie der Maßtheorie und der Funktionalanalysis verwendet werden. In seiner klassischen Fassung sagt er aus, dass sich vollständige metrische Räume nicht als abzählbare Vereinigung von mageren Mengen darstellen lassen. Der Begriff der mageren Menge verallgemeinert dabei den Begriff der nirgends dichten Menge.
Der Satz wurde 1899 von René Louis Baire für den Spezialfall des euklidischen Raumes
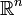 bewiesen. Der vorliegende Artikel enthält die genannte klassische Kernaussage des baireschen Satzes, erläutert die baireschen Kategorien („magere“ und „fette“ Mengen) und geht schließlich auf moderne Verallgemeinerungen des Satzes ein.
bewiesen. Der vorliegende Artikel enthält die genannte klassische Kernaussage des baireschen Satzes, erläutert die baireschen Kategorien („magere“ und „fette“ Mengen) und geht schließlich auf moderne Verallgemeinerungen des Satzes ein.Inhaltsverzeichnis
Bairescher Satz für metrische Räume
- Sei
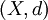 ein vollständiger metrischer Raum und
ein vollständiger metrischer Raum und 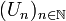 eine Folge offener und dichter Teilmengen von
eine Folge offener und dichter Teilmengen von 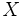 . Dann ist auch
. Dann ist auch 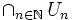 dicht in
dicht in 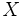 .
. - Sei
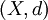 ein vollständiger metrischer Raum und
ein vollständiger metrischer Raum und 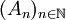 eine Folge abgeschlossener Teilmengen von
eine Folge abgeschlossener Teilmengen von 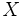 mit
mit 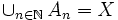 . Dann gibt es ein
. Dann gibt es ein 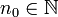 so, dass
so, dass 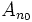 eine offene Kugel enthält – mit anderen Worten: die Folge
eine offene Kugel enthält – mit anderen Worten: die Folge 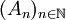 kann nicht nur aus nirgends dichten Teilmengen bestehen.
kann nicht nur aus nirgends dichten Teilmengen bestehen.
Die beiden Formulierungen des Satzes sind äquivalent und ordnungstheoretisch dual zueinander.
Bairesche Kategorien
Sei
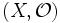 ein topologischer Raum (insbesondere z.B. ein metrischer Raum).
ein topologischer Raum (insbesondere z.B. ein metrischer Raum).- Eine Teilmenge
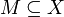 heißt von 1. Baire-Kategorie (oder mager), falls es eine Folge
heißt von 1. Baire-Kategorie (oder mager), falls es eine Folge 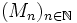 von nirgends dichten Teilmengen mit
von nirgends dichten Teilmengen mit 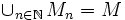 gibt.
gibt. - Falls eine Teilmenge
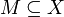 nicht von 1. Baire-Kategorie ist, dann heißt sie von 2. Baire-Kategorie (oder fett).
nicht von 1. Baire-Kategorie ist, dann heißt sie von 2. Baire-Kategorie (oder fett).
Beispiele fetter und magerer Mengen
- Die Teilmenge
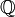 der rationalen Zahlen ist mager in
der rationalen Zahlen ist mager in 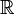 , die Menge der irrationalen Zahlen
, die Menge der irrationalen Zahlen 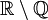 ist fett in
ist fett in 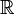 .
. 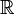 ist fett in
ist fett in 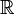 aber mager in
aber mager in 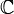 .
.- Die Cantormenge ist eine nicht abzählbare, abgeschlossene und nirgends dichte, magere Teilmenge von
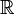 .
.
Bairescher Kategoriensatz
Mit Hilfe der baireschen Kategorien lässt sich der Satz von Baire für metrische Räume auch so formulieren:
- In einem vollständigen metrischen Raum liegt das Komplement einer Menge von 1. Baire-Kategorie dicht und ein nicht-leerer vollständiger metrischer Raum ist in sich selbst von 2. Baire-Kategorie.
Verallgemeinerung: Bairescher Raum
Losgelöst von metrischen Begriffen heißt ein topologischer Raum X bairescher Raum, wenn er eine der folgenden äquivalenten Bedingungen erfüllt:
- Die Vereinigung einer abzählbaren Familie abgeschlossener Teilmengen von X ohne innere Punkte hat keinen inneren Punkt.
- Der Durchschnitt einer abzählbaren Familie offener, dichter Teilmengen von X ist immer noch dicht in X.
- Eine offene, nichtleere Teilmenge von X ist niemals mager.
- Das Komplement einer mageren Teilmenge von X ist dicht in X.
Beispiele für bairesche Räume
- Jeder vollständige metrische Raum.
- Jeder topologische Raum, der zu einem vollständigen metrischen Raum homöomorph ist, also jeder metrisierbare topologische Raum, der bezüglich dieser Metrik vollständig ist.
- Jeder lokalkompakte Hausdorffraum.
-
- (Auch die Feststellung, dass die genannten topologischen Räume bairesche Räume sind, wird – etwa in Camps (2006) – als „Satz von Baire“ bezeichnet.)
Anwendungen
Der Satz von Baire ermöglicht elegante Beweise zentraler Sätze der klassischen Funktionalanalysis:
- Basis eines Banachraums
Als einfaches Beispiel der Anwendung des Satzes von Baire soll gezeigt werden, dass jeder unendlich-dimensionale Banachraum eine überabzählbare Basis hat.
Beweis durch die Gegenannahme, es gäbe eine abzählbare Basis
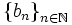 des Banachraumes
des Banachraumes 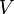 . Sei
. Sei 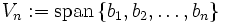 . Dann gilt:
. Dann gilt:- als endlich-dimensionale Vektorräume sind die
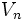 abgeschlossen,
abgeschlossen, - ihre Vereinigung ergibt den ganzen Raum:
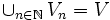 .
.
Nach dem Satz von Baire muss einer der
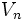 eine Kugel enthalten. Ein Untervektorraum, der eine Kugel enthält, ist aber immer der ganze Raum. Dadurch würde
eine Kugel enthalten. Ein Untervektorraum, der eine Kugel enthält, ist aber immer der ganze Raum. Dadurch würde 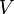 zu einem endlichdimensionalen Raum, was zu einem Widerspruch führt.
zu einem endlichdimensionalen Raum, was zu einem Widerspruch führt.Vergleichbare Begriffsbildungen in der Maßtheorie
In der Maßtheorie wird gezeigt, dass sich der Raum
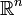 , versehen mit dem Hausdorff- bzw. Lebesgue-Maß nicht als abzählbare Vereinigung von Nullmengen schreiben lässt. Ersetzt man hier den Begriff Nullmenge durch magere Menge, erhält man in diesem Spezialfall die Aussage des baireschen Kategoriensatzes. Die baireschen Kategorien können somit als topologisches Analogon zu Nullmengen bzw. Maßräumen in der Maßtheorie gesehen werden. In der Tat bestehen weitreichende Gemeinsamkeiten. Diese werden in Oxtoby (1980) ausführlich beschrieben.
, versehen mit dem Hausdorff- bzw. Lebesgue-Maß nicht als abzählbare Vereinigung von Nullmengen schreiben lässt. Ersetzt man hier den Begriff Nullmenge durch magere Menge, erhält man in diesem Spezialfall die Aussage des baireschen Kategoriensatzes. Die baireschen Kategorien können somit als topologisches Analogon zu Nullmengen bzw. Maßräumen in der Maßtheorie gesehen werden. In der Tat bestehen weitreichende Gemeinsamkeiten. Diese werden in Oxtoby (1980) ausführlich beschrieben.Literatur
- Dirk Werner: Funktionalanalysis. Springer Verlag, 2005. ISBN 3-540-43586-7
- J. C. Oxtoby: Measure and Category. Springer Verlag, 1980. ISBN 3-540-90508-1
- Sei
Wikimedia Foundation.
