- Balancierter Suchbaum
-
Ein Balancierter Baum ist in der Informatik ein Spezialfall der Datenstruktur Baum, der eine maximale Höhe von
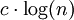 garantiert, wobei n die Anzahl der Elemente im Baum angibt und c eine von n unabhängige Konstante ist.
garantiert, wobei n die Anzahl der Elemente im Baum angibt und c eine von n unabhängige Konstante ist.Inhaltsverzeichnis
Problem: Entartung
Die wichtigste Anwendung von Bäumen in der Informatik ist die als Suchbaum. Die Laufzeit der wichtigsten Operationen in einem Suchbaum (Einfügen, Suchen oder Löschen eines Wertes) hängt im schlechtesten Fall linear von der Höhe des Baumes ab (die Operationen haben eine Komplexität von O(h); h Höhe des Baumes).
Jeder k-näre Baum mit n Knoten hat eine Höhe von
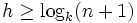 ; und im Durchschnitt immer noch
; und im Durchschnitt immer noch 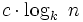 für ein gewisses konstantes c. So sind auch die Operationen auf einem Baum mindestens der Komplexität O(logkn) = O(logn).
für ein gewisses konstantes c. So sind auch die Operationen auf einem Baum mindestens der Komplexität O(logkn) = O(logn).Fügt man jedoch zum Beispiel einem Suchbaum eine große Menge bereits sortierter Daten ein, wächst dieser ungleichmäßig und hat im Extremfall eine Höhe von n mit der unerwünschten Folge, dass auch jede folgende Einfüge-, Such- und Löschoperation der Komplexität O(n) ist.
Siehe auch: O-Notation, Komplexität, Erwartungswert
Gegenstrategie: Balance halten
Balancierte Bäume wurden entwickelt, um die Entartung zu verhindern und eine Höhe von
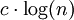 zu garantieren.
zu garantieren.Dazu verfolgt man unterschiedliche Konzepte. Allen gemeinsam ist: Man fordert spezielle Eigenschaften des Baumes,
- aus denen folgt, dass die Höhe des Baumes in jedem Fall
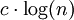 ist.
ist. - sodass es geeignete Einfüge-, Such- und Löschoperationen (sinnvollerweise der Komplexität O(h)) gibt, die die speziellen Eigenschaften wahren.
Man erhält eine solche Operation, indem man die Operation der allgemeinen Suchbäume verwendet und nach jeder Ausführung den Baum an der Stelle der Änderung neu balanciert.
Höhenbalance
Nach der Höhe balancierte Bäume stellen für jeden Knoten sicher, dass die Höhe des linken Unterbaumes und die Höhe des rechten Unterbaumes nur um ein bestimmtes Verhältnis oder eine bestimmte Differenz voneinander abweichen.
Beim Rot-Schwarz-Baum wird jedem Knoten eine Farbe (rot oder schwarz) zugeordnet; der Baum ist bezüglich der schwarzen Knoten optimal höhenbalanciert und der Anteil der roten Knoten ist begrenzt. Diese Bäume stellen eine binäre Realisierung der 2-3-4-Bäume dar, einer speziellen Variante der B-Bäume.
Im AVL-Baum gilt für jeden Knoten: Die Höhe seines linken Kindes weicht von der seines rechten Kindes um höchstens ±1 ab.
Gewichtsbalance
In einem gewichtsbalancierten Baum (BB-Baum) gilt für jeden Knoten: Die Anzahl der Knoten (das Gewicht) links unter ihm steht in einem gewissen Verhältnis zu der Gesamtanzahl der Knoten unter ihm (und damit auch in einem gewissen Verhältnis zu der Anzahl der Knoten rechts unter ihm).
- aus denen folgt, dass die Höhe des Baumes in jedem Fall
Wikimedia Foundation.


