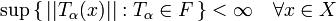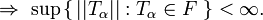- Banach-Steinhaus
-
Der Satz von Banach-Steinhaus oder das Prinzip der gleichmäßigen Beschränktheit ist eines der fundamentalen Ergebnisse der Funktionalanalysis und bildet zusammen mit dem Satz von Hahn-Banach und dem Offenheitssatz einen der Eckpfeiler des Gebiets. Er besagt in seiner Grundform, dass für eine Familie stetiger, linearer Operatoren auf einem Banachraum punktweise Beschränktheit äquivalent zu Beschränktheit ist.
Hugo Steinhaus und Stefan Banach veröffentlichten den Satz 1927. Er wurde jedoch unabhängig davon auch von Hans Hahn bewiesen.
Inhaltsverzeichnis
Satz von Banach-Steinhaus
Sei X ein Banachraum, N ein normierter Vektorraum und F eine Familie stetiger, linearer Operatoren von X nach N.
Dann gilt:
Beweis
Unter Verwendung des Baire'schen Kategoriensatzes:
- Für
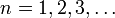 sei
sei 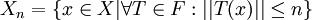 . Nach Annahme ist die Vereinigung aller Xn gleich X.
. Nach Annahme ist die Vereinigung aller Xn gleich X. - Da X von 2. Baire-Kategorie ist, hat eines der Xn einen inneren Punkt, d.h. es gibt ein δ > 0 und ein
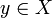 , sodass
, sodass 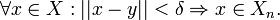
- Für jedes z mit | | z | | < δ gilt dann:
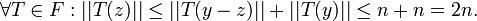
- Also ist
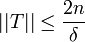 für alle
für alle 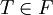 , sodass
, sodass 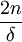 eine gleichmäßige Schranke für die Menge F ist.
eine gleichmäßige Schranke für die Menge F ist.
Verallgemeinerung
Die allgemeine Form des Satzes gilt für tonnelierte Räume (auch als gefasste Räume bezeichnet):
X sei ein gefasster Raum, Y ein lokal konvexer Raum. Dann gilt: Jede Familie punktweise beschränkter, stetiger, linearer Operatoren von X nach Y ist gleichgradig stetig (sogar gleichmäßig gleichgradig stetig).
Dabei werden folgende Definitionen verwendet:Eine Teilmenge S eines topologischen Vektorraums heißt Tonne oder gefasst , falls sie konvex, balanciert (d. h.
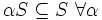 mit
mit 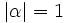 ), absorbierend (d. h.
), absorbierend (d. h. 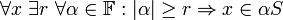 ) und abgeschlossen ist. Die Eigenschaften konvex und balanciert können auch mit der Eigenschaft absolutkonvex zusammengefasst werden.
) und abgeschlossen ist. Die Eigenschaften konvex und balanciert können auch mit der Eigenschaft absolutkonvex zusammengefasst werden.Ein topologischer Vektorraum heißt gefasst oder tonneliert, falls jede gefasste Menge (Tonne) eine Umgebung des Nullvektors ist. Tonnelierte Räume sind lokal konvex.
Literatur
- Stefan Banach, Hugo Steinhaus. "Sur le principle de la condensation de singularités". Fundamenta Mathematicae, 9 50-61, 1927.
Wikimedia Foundation.