- Banach-Tarski Paradox
-
Das Banach-Tarski-Paradoxon oder auch Satz von Banach und Tarski ist eine Aussage der Mathematik, die demonstriert, dass sich der anschauliche Volumenbegriff nicht auf beliebige Punktmengen verallgemeinern lässt. Danach kann man eine Kugel derart zerlegen, dass sich ihre Teile wieder zu zwei lückenlosen Kugeln zusammenfügen lassen, von denen jede denselben Durchmesser hat wie die ursprüngliche. Das Volumen verdoppelt sich, ohne dass anschaulich ersichtlich ist, wie durch diesen Vorgang Volumen aus dem Nichts entstehen können sollte. Dieses Paradoxon demonstriert, dass das mathematische Modell des Raumes als Punktmenge in der Mathematik Aspekte hat, die sich in der physischen Realität nicht wiederfinden.
Im mathematischen Formalismus wird das Paradoxon damit erklärt, dass die Kugelteile dermaßen kompliziert geformt sind, dass ihr Volumen nicht mehr definierbar ist. Man bezeichnet solche Punktmengen als nicht messbar. Sie sind in einem gewissen Sinne unendlich filigran und porös bzw. staubwolkenartig. Die mathematische Existenz solcher Mengen ist nicht selbstverständlich: Zum Beweis der Existenz von nicht messbaren Teilmengen im d-dimensionalen, reellen Raum
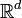 benötigt man das Auswahlaxiom, das zwar von einer überwiegenden Mehrheit der Mathematiker, jedoch nicht von allen, akzeptiert wird. Messbare Punktmengen hingegen verhalten sich hinsichtlich ihres Volumens additiv.
benötigt man das Auswahlaxiom, das zwar von einer überwiegenden Mehrheit der Mathematiker, jedoch nicht von allen, akzeptiert wird. Messbare Punktmengen hingegen verhalten sich hinsichtlich ihres Volumens additiv.Die polnischen Mathematiker Stefan Banach und Alfred Tarski führten den Beweis 1924 und zeigten, dass im Fall der Kugel eine Zerlegung in sechs Teile ausreichend ist. Für diesen Satz kann es jedoch lediglich einen Existenzbeweis geben, ein konstruktiver Beweis ist nicht möglich.
In einer allgemeineren Formulierung dieses Satzes können sich Ausgangs- und Endkörper durch einen beliebigen Volumenfaktor unterscheiden und bis auf gewisse Einschränkungen auch beliebige, verschiedene Gestalt besitzen. Die allgemeine Formulierung dieses mathematischen Satzes in Räumen mit drei und mehr Dimensionen lautet:
Sei
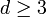 eine ganze Zahl und seien
eine ganze Zahl und seien 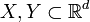 beschränkte Mengen mit nicht-leerem Inneren. Dann gibt es eine natürliche Zahl n und eine disjunkte Zerlegung
beschränkte Mengen mit nicht-leerem Inneren. Dann gibt es eine natürliche Zahl n und eine disjunkte Zerlegung 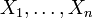 von X und zugehörige Bewegungen
von X und zugehörige Bewegungen  derart, dass Y die disjunkte Vereinigung der Mengen
derart, dass Y die disjunkte Vereinigung der Mengen  ist.
ist.In der Ebene ist dieser Satz nicht gültig. 1990 konnte Miklós Laczkovich jedoch zeigen, dass dieser Satz für Flächen zumindest in ähnlicher Form gilt. Danach sind zwei Flächen, sofern ihr Rand hinreichend glatt ist, ebenfalls zerlegungsgleich, allerdings nur dann, wenn ihre Flächen gleich groß sind. In diesem Sinne ist beispielsweise eine Quadratur des Kreises möglich, wenn auch nicht mit Zirkel und Lineal. Die Anzahl der erforderlichen Teile wurde jedoch von Laczkovich auf etwa 1050 geschätzt.
Weblinks
- Reinhard Winkler: Wie macht man 2 aus 1? – Herleitung mit den Mitteln der Schulmathematik, in html- und pdf-Version.
- Eine Kugel ist eine Kugel ist... sind zwei Kugeln?! – Das Paradoxon von Banach-Tarski auf dem Matheplaneten u. A. mit einer Konstruktion der benötigten Zerlegung der Kugel.
Wikimedia Foundation.

