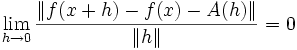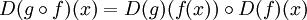- Banachraum
-
Banach-Raum berührt die Spezialgebiete
hat Eigenschaften von
ist Spezialfall von
umfasst als Spezialfälle
Ein Banach-Raum, benannt nach dem Mathematiker Stefan Banach, ist ein vollständiger normierter Vektorraum.
Banach-Räume gehören zu den zentralen Studienobjekten der Funktionalanalysis. Die interessantesten Banach-Räume sind unendlich-dimensionale Funktionenräume.
Inhaltsverzeichnis
Definitionen
Ein Banach-Raum ist ein Vektorraum V über einem Körper K (normalerweise die reellen oder komplexen Zahlen) mit einer Norm und einer durch diese Norm induzierten Metrik, bezüglich der jede Cauchy-Folge aus Elementen von V gegen ein Element von V konvergiert.
Erläuterungen
Ein Banachraum ist also ein normierter Vektorraum, der bezüglich der durch die Norm induzierten Metrik vollständig ist.
Bei metrischen Räumen ist die Vollständigkeit eine Eigenschaft der Metrik, nicht des topologischen Raums selbst. Geht man zu einer äquivalenten Metrik (das heißt zu einer Metrik, die dieselbe Topologie erzeugt) über, kann die Vollständigkeit verloren gehen. Für zwei äquivalente Normen auf einem normierten Raum hingegen gilt, dass die eine genau dann vollständig ist, wenn auch die andere es ist. Im Falle der normierten Räume ist die Vollständigkeit daher eine Eigenschaft der Normtopologie, die nicht von der konkreten Norm abhängt. Ein Banachraum ist ein vollständiger normierter Raum, ohne dass man dazu auf eine konkrete Norm Bezug nehmen muss.
Beispiele
Im Folgenden sei K einer der Körper
 oder
oder 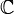 .
.- Die Euklidischen und unitären Räume Kn sind mit der 2-Norm
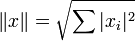 Banach-Räume.
Banach-Räume. - Der Raum aller stetigen Funktionen
![f: [a,b]\to K](/pictures/dewiki/98/b25246670a92546effd2e51085df85db.png) auf einem kompakten Intervall wird mit der Supremumsnorm
auf einem kompakten Intervall wird mit der Supremumsnorm ![\|f\| = \operatorname{sup} \{|f(x)|: x\in [a,b]\}](/pictures/dewiki/97/a396159b8178dc2ec45857a503059c72.png) zu einem Banach-Raum. Dies ist in der Tat eine Norm, da stetige Funktionen auf einem kompakten Intervall beschränkt sind. Der Raum ist vollständig unter dieser Norm und der resultierende Banach-Raum wird geschrieben als C[a,b].
zu einem Banach-Raum. Dies ist in der Tat eine Norm, da stetige Funktionen auf einem kompakten Intervall beschränkt sind. Der Raum ist vollständig unter dieser Norm und der resultierende Banach-Raum wird geschrieben als C[a,b]. - Das vorige Beispiel kann auf den Raum C(X) aller stetiger Funktionen
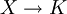 verallgemeinert werden, wobei X ein kompakter Raum ist, oder auf den Raum aller beschränkten stetigen Funktionen
verallgemeinert werden, wobei X ein kompakter Raum ist, oder auf den Raum aller beschränkten stetigen Funktionen 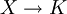 , wobei X ein beliebiger topologischer Raum ist, oder sogar auf den Raum B(X) aller beschränkten Funktionen
, wobei X ein beliebiger topologischer Raum ist, oder sogar auf den Raum B(X) aller beschränkten Funktionen 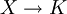 auf einer beliebigen Menge X. In diesen Beispielen kann man Funktionen multiplizieren und im selben Raum bleiben. Diese Räume sind somit sogar so genannte Banach-Algebren.
auf einer beliebigen Menge X. In diesen Beispielen kann man Funktionen multiplizieren und im selben Raum bleiben. Diese Räume sind somit sogar so genannte Banach-Algebren. - Der Folgenraum
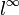 besteht aus allen beschränkten Folgen mit Elementen aus K; die Norm solch einer Folge ist definiert als das Supremum der Absolutbeträge der Elemente der Folge. Dieser Banachraum ist der Spezialfall
besteht aus allen beschränkten Folgen mit Elementen aus K; die Norm solch einer Folge ist definiert als das Supremum der Absolutbeträge der Elemente der Folge. Dieser Banachraum ist der Spezialfall 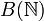 des vorangegangenen Beispiels.
des vorangegangenen Beispiels. - Sei
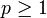 eine reelle Zahl, so kann man den Raum aller Folgen (
eine reelle Zahl, so kann man den Raum aller Folgen (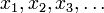 ) mit Elementen aus K betrachten, welche die Eigenschaft haben, dass die unendliche Reihe
) mit Elementen aus K betrachten, welche die Eigenschaft haben, dass die unendliche Reihe 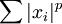 konvergiert. Die p-te Wurzel des Wertes dieser Reihe sei dann definiert als die p-Norm der Folge. Der Folgenraum zusammen mit dieser Norm ist ein Banach-Raum; er wird bezeichnet mit
konvergiert. Die p-te Wurzel des Wertes dieser Reihe sei dann definiert als die p-Norm der Folge. Der Folgenraum zusammen mit dieser Norm ist ein Banach-Raum; er wird bezeichnet mit 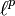 .
. - Ist
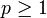 eine reelle Zahl ist, so kann man alle Funktionen
eine reelle Zahl ist, so kann man alle Funktionen ![f : [a, b] \to K](/pictures/dewiki/98/b25246670a92546effd2e51085df85db.png) betrachten, für | f | p Lebesgue-integrierbar ist. Die p-te Wurzel aus diesem Integral nennt man dann die p-Norm von f, die üblicher Weise mit
betrachten, für | f | p Lebesgue-integrierbar ist. Die p-te Wurzel aus diesem Integral nennt man dann die p-Norm von f, die üblicher Weise mit 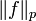 bezeichnet wird. Dabei handelt es sich nicht um eine Norm, sondern nur um eine sogenannte Halbnorm, denn es gibt Funktionen, die nicht Null sind, wohl aber ihre p-Norm. Man definiert eine Äquivalenzrelation wie folgt: f und g sind äquivalent genau dann, wenn die Norm von f − g Null ist. Die Menge der Äquivalenzklassen [f] solcher Funktionen mit der durch
bezeichnet wird. Dabei handelt es sich nicht um eine Norm, sondern nur um eine sogenannte Halbnorm, denn es gibt Funktionen, die nicht Null sind, wohl aber ihre p-Norm. Man definiert eine Äquivalenzrelation wie folgt: f und g sind äquivalent genau dann, wenn die Norm von f − g Null ist. Die Menge der Äquivalenzklassen [f] solcher Funktionen mit der durch ![\|[f]\|_p:= \|f\|_p](/pictures/dewiki/49/1c9bf1d7b7f3fa97f169678cea7249e3.png) erklärten Norm bildet dann einen Banach-Raum, der mit Lp[a,b] bezeichnet wird. Es ist entscheidend, hier den Raum der Lebesgue-integrierbaren Funktionen zu betrachten und nicht den Raum der Riemann-integrierbaren Funktionen, denn im zweiten Fall erhält man keinen vollständigen Raum.
erklärten Norm bildet dann einen Banach-Raum, der mit Lp[a,b] bezeichnet wird. Es ist entscheidend, hier den Raum der Lebesgue-integrierbaren Funktionen zu betrachten und nicht den Raum der Riemann-integrierbaren Funktionen, denn im zweiten Fall erhält man keinen vollständigen Raum.
Lineare Operatoren
Sind V und W Banach-Räume über demselben Körper K, so wird die Menge aller stetigen K-linearen Abbildungen
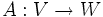 mit L(V,W) bezeichnet.
mit L(V,W) bezeichnet.In unendlich-dimensionalen Räumen sind lineare Abbildungen nicht notwendigerweise stetig.
L(V, W) ist ein K-Vektorraum, und durch ||A|| = sup { ||Ax|| : x in V mit ||x|| ≤ 1 } ist eine Norm auf L(V, W) definiert. Ist W ein Banach-Raum, so auch L(V, W).
Ist V ein Banach-Raum, so ist L(V) = L(V,V) eine unitäre Banach-Algebra; die Multiplikationsoperation ist durch die Komposition linearer Abbildungen gegeben.
Ableitungen
Es ist möglich die Ableitung einer Funktion f : V → W zwischen zwei Banachräumen zu definieren. Intuitiv sieht man, dass, falls x ein Element von V ist, die Ableitung von f im Punkt x eine stetige lineare Abbildung ist, die f nahe x in der Ordnung des Abstandes
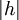 approximiert.
approximiert.Man nennt f (Fréchet)-differenzierbar in x, falls eine stetige lineare Abbildung
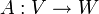 existiert, so dass
existiert, so dassgilt. Der Grenzwert wird hier über alle Folgen mit nicht-Null-Element aus V gebildet, die gegen 0 konvergieren. Falls der Grenzwert existiert, schreibt man Df(x) = A und nennt es die (Fréchet)-Ableitung von f in x. Weitere Verallgemeinerungen der Ableitung ergeben sich analog zur Analysis auf endlich-dimensionalen Räumen. Gemeinsam für alle Ableitungsbegriffe ist aber die Frage nach der Stetigkeit der linearen Abbildung Df(x)
Dieser Begriff der Ableitung ist eine Verallgemeinerung der gewöhnlichen Ableitung von Funktionen
 , da die linearen Abbildungen von
, da die linearen Abbildungen von  auf
auf  einfach Multiplikationen mit reellen Zahlen sind.
einfach Multiplikationen mit reellen Zahlen sind.Falls f differenzierbar ist in jedem Punkt x aus V, dann ist Df : V → L(V, W) eine weitere Abbildung zwischen Banachräumen (im Allgemeinen keine lineare Abbildung!), und kann möglicherweise erneut differenziert werden, wodurch die höheren Ableitungen von f definiert werden. Die n-te Ableitung im Punkt x kann somit als multilineare Abbildung
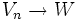 gesehen werden.
gesehen werden.Differentiation ist eine lineare Operation im folgenden Sinne: sind f und g zwei Abbildungen V - W, die in x differenzierbar sind, und r und s sind Skalare aus K, dann ist rf + sg differenzierbar in x mit D(rf + sg)(x) = rD(f)(x) + sD(g)(x).
Die Kettenregel ist in diesem Zusammenhang ebenfalls gültig. Wenn
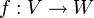 eine in
eine in 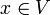 und
und 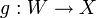 eine in f(x) differenzierbare Funktion ist, dann ist die Komposition
eine in f(x) differenzierbare Funktion ist, dann ist die Komposition  in x differenzierbar und die Ableitung ist die Komposition der Ableitungen:
in x differenzierbar und die Ableitung ist die Komposition der Ableitungen:Dualer Raum
Ist V ein Banach-Raum und K der zugrundeliegende Körper, dann ist K selbst ebenfalls ein Banach-Raum (mit dem Absolutbetrag als Norm), und man kann den dualen Raum definieren durch V' = L(V,K). Dieser ist wiederum ein Banach-Raum. Er kann verwendet werden, um eine Topologie auf V zu definieren: die schwache Topologie. Die schwache Topologie ist nicht äquivalent zur Normtopologie auf V, wenn der Raum V unendlichdimensional ist. Aus der Konvergenz einer Folge in der Normtopologie folgt immer die Konvergenz in der schwachen Topologie, umgekehrt im Allgemeinen nicht. In diesem Sinne ist die Konvergenzbedingung, die sich aus der schwachen Topologie ergibt "schwächer".
Es gibt eine natürliche Abbildung F von V nach V'' = (V')' = L(V',K) (der Bidualraum), definiert durch:
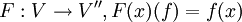 für alle x aus V und f aus V'. Aus dem Satz von Hahn-Banach folgt, dass für jedes x aus V die Abbildung
für alle x aus V und f aus V'. Aus dem Satz von Hahn-Banach folgt, dass für jedes x aus V die Abbildung 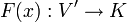 stetig ist und daher ein Element von V''. Die Abbildung F ist stets injektiv und stetig (sogar isometrisch); falls sie zudem noch surjektiv ist (und somit ein isometrischer Isomorphismus), so nennt man den Banachraum V reflexiv. Reflexive Banachräume haben viele wichtige geometrische Eigenschaften.
stetig ist und daher ein Element von V''. Die Abbildung F ist stets injektiv und stetig (sogar isometrisch); falls sie zudem noch surjektiv ist (und somit ein isometrischer Isomorphismus), so nennt man den Banachraum V reflexiv. Reflexive Banachräume haben viele wichtige geometrische Eigenschaften.Ein Banachraum ist reflexiv genau dann wenn sein Dualraum reflexiv ist. Äquivalent zu diesen Aussagen ist weiterhin, dass die Einheitskugel von V in der schwachen Topologie kompakt ist.
Einordnung in die Hierarchie mathematischer Strukturen
Jeder Hilbert-Raum ist ein Banach-Raum, aber nicht umgekehrt: ein Banach-Raum ist genau dann ein Hilbert-Raum, wenn in ihm die Parallelogrammgleichung zumindest für eine äquivalente Norm gilt.
Einige wichtige Räume in der Funktionalanalysis, zum Beispiel der Raum aller unendlich oft differenzierbaren Funktionen
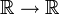 oder der Raum aller Distributionen auf
oder der Raum aller Distributionen auf 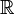 , sind zwar vollständig, aber keine normierten Vektorräume und daher keine Banachräume. In Fréchet-Räumen hat man noch eine vollständige Metrik, während LF-Räume vollständige uniforme Vektorräume sind, die als Grenzfälle von Fréchet-Räumen auftauchen. Es handelt sich hierbei um lokalkonvexe Räume.
, sind zwar vollständig, aber keine normierten Vektorräume und daher keine Banachräume. In Fréchet-Räumen hat man noch eine vollständige Metrik, während LF-Räume vollständige uniforme Vektorräume sind, die als Grenzfälle von Fréchet-Räumen auftauchen. Es handelt sich hierbei um lokalkonvexe Räume.Literatur
- Stefan Banach: Théorie des opérations linéaires. Warszawa 1932. (Monografie Matematyczne; 1) Zbl 0005.20901 (Kolmogoroff)
- Die Euklidischen und unitären Räume Kn sind mit der 2-Norm
Wikimedia Foundation.