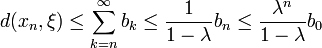- Banachscher Fixpunktsatz
-
Der Fixpunktsatz von Banach ist ein Satz aus der Mathematik. Er ist nach dem Mathematiker Stefan Banach benannt und enthält eine Existenz-, eine Konstruktions- und eine Fehleraussage für Fixpunktprobleme.
Eine Veranschaulichung des Satzes liefert eine Landkarte, auf der die Umgebung, in der man sich befindet, abgebildet ist. Sieht man diese Karte als Kontraktion der Umgebung, so findet man genau einen Punkt auf der Karte, der mit dem direkt darunter liegenden Punkt in der realen Welt übereinstimmt.
Inhaltsverzeichnis
Aussagen des Fixpunktsatzes
Existenz und Eindeutigkeit: Eine Kontraktion
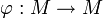 eines (nichtleeren) vollständigen metrischen Raumes M besitzt genau einen Fixpunkt, also einen Punkt
eines (nichtleeren) vollständigen metrischen Raumes M besitzt genau einen Fixpunkt, also einen Punkt 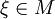 mit
mit 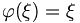 .
.Dabei ist:
- zum Beispiel jeder Banachraum, und unter diesen jeder normierte endlichdimensionale reelle oder komplexe Vektorraum, ein vollständiger metrischer Raum,
- eine Kontraktion eine Abbildung
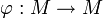 , welche Lipschitz-stetig mit einer Konstanten
, welche Lipschitz-stetig mit einer Konstanten 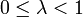 ist.
ist.
Konstruktion: Für jeden Startwert
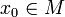 konvergiert die Folge (xn) mit
konvergiert die Folge (xn) mit 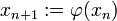 gegen ξ.
gegen ξ.Fehlerabschätzung: Es gibt die folgenden Abschätzungen für den Abstand des Fixpunktes zur rekursiven Folge:
- A-priori-Abschätzung
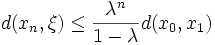 (u.a. auch für n=0)
(u.a. auch für n=0)- für den n-ten Fehler durch die ersten beiden Folgenglieder und die
- A-posteriori-Abschätzung
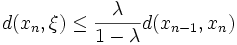
- für den n-ten Fehler durch die beiden zuletzt bestimmten Folgenglieder.
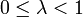 ist dabei die Kontraktionskonstante bzw. Lipschitz-Konstante.
ist dabei die Kontraktionskonstante bzw. Lipschitz-Konstante.Bemerkung: Oft wird dieser Satz nicht allgemein auf (vollständigen) metrischen Räumen, sondern auf einem Banach-Raum B, also einem vollständigen normierten Vektorraum, oder einer Teilmenge M⊆B davon formuliert. Der einzige Unterschied ist, dass der Abstand dann durch die Norm der Differenz erklärt ist,
 .
.Zum Beweis
Beweisidee für normierte Räume
Um den Beweisgang zu verstehen, ist es hilfreich, zunächst in einem Banach-Raum zu operieren. Die eigentlichen Beweisschritte können dann auch im metrischen Raum vollzogen werden. Wir konstruieren die rekursive Folge
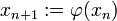 mit irgendeinem Startpunkt
mit irgendeinem Startpunkt 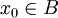 . Diese fassen wir als Partialsummen einer (Teleskop-)Reihe auf, deren Glieder die Differenzen
. Diese fassen wir als Partialsummen einer (Teleskop-)Reihe auf, deren Glieder die Differenzen 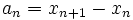 sind,
sind, 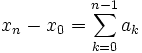 . Von der Reihe zeigen wir, dass sie eine geometrische Reihe als Majorante hat. Wegen der Vollständigkeit des Raumes folgt daraus die Konvergenz der Reihe, der Punkt
. Von der Reihe zeigen wir, dass sie eine geometrische Reihe als Majorante hat. Wegen der Vollständigkeit des Raumes folgt daraus die Konvergenz der Reihe, der Punkt 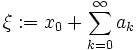 ist der gesuchte Fixpunkt.
ist der gesuchte Fixpunkt.Beweis im metrischen Raum
Wir betrachten das Problem im vollständigen metrischen Raum. Wieder konstruieren wir die rekursive Folge. Statt direkt mit Teleskopsummen zu operieren, betrachten wir die Abstände
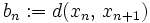 . Die mehrfache Anwendung der Dreiecksungleichung auf die Differenz beliebiger Folgenglieder liefert
. Die mehrfache Anwendung der Dreiecksungleichung auf die Differenz beliebiger Folgenglieder liefert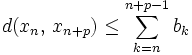 .
.
Zeigen wir also, dass die Reihe
 konvergiert, genauer eine geometrische Reihe als Majorante hat, so ist
konvergiert, genauer eine geometrische Reihe als Majorante hat, so ist 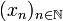 eine Cauchy-Folge und damit konvergent. Nach Voraussetzung der Kontraktivität gilt:
eine Cauchy-Folge und damit konvergent. Nach Voraussetzung der Kontraktivität gilt: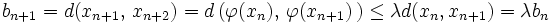 .
.
Also ist
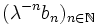 eine monoton fallende Folge, mithin
eine monoton fallende Folge, mithin 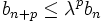 , insbesondere
, insbesondere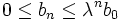 ,
, 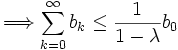 wegen λ<1.
wegen λ<1.
Es gibt also den Grenzwert
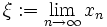 . Für die Abschätzungen erhalten wir
. Für die Abschätzungen erhalten wirInsbesondere ist
 , also
, also 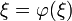 tatsächlich ein Fixpunkt. Für einen weiteren möglichen Fixpunkt η gilt
tatsächlich ein Fixpunkt. Für einen weiteren möglichen Fixpunkt η gilt 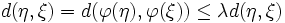 , was nur bei η = ξ möglich ist
, was nur bei η = ξ möglich istAnwendungen
Dieser Satz wird in vielen konstruktiven Sätzen der Analysis benutzt, die wichtigsten sind:
- das inverse- und implizite-Funktionen-Theorem
- der Existenz- und Eindeutigkeitssatz von Picard-Lindelöf für gewöhnliche Differentialgleichungen
Wikimedia Foundation.