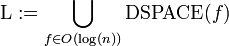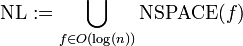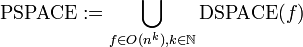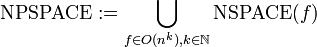- Bandkomplexität
-
Unter der Platzkomplexität eines Problems versteht man den (minimalen) Bedarf an Speicherplatz eines Algorithmus' zur Lösung dieses Problems, in Abhängigkeit von der Länge der Eingabe. Es interessiert also nicht der Speicherbedarf eines konkreten Programms auf einem bestimmten Computer, sondern vielmehr, wie der Speicheraufwand wächst, wenn mehr Daten zu verarbeiten sind. Also z. B. ob sich der Aufwand für die doppelte Datenmenge verdoppelt oder quadriert (siehe auch Skalierbarkeit).
Inhaltsverzeichnis
Notation
Die Platzkomplexität wird immer in Bezug auf ein Maschinenmodell angegeben. In der Regel ist das Bezugsmodell die Turingmaschine. Es gelten die folgenden Notationen:
- Mit DSPACE(f) werden alle Probleme bezeichnet, die von einer deterministischen Turingmaschine entschieden werden können, die bei einer Eingabe der Länge n höchstens f(n) Speicherzellen für die Berechnung benutzt hat.
- Mit NSPACE(f) werden alle Probleme bezeichnet, die von einer nicht-deterministischen Turingmaschine entschieden werden können, die bei einer Eingabe der Länge n höchstens f(n) Speicherzellen für die Berechnung benutzt hat.
Aus diesen Klassen, lassen sich u. a. folgende Platzkomplexitätsklassen bilden:
Es gibt darüber hinaus noch weitere Platzkomplexitätsklassen, die sich auf exponentiellen oder gar über-exponentiellen Speicherplatz beziehen.
Beziehungen
Die Komplexitätsklassen der Zeitkomplexität stehen mit denen der Platzkomplexität in folgender Beziehung:
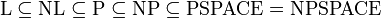
Sonstiges
In der Komplexitätstheorie ist die Platzkomplexität neben der Zeitkomplexität ein wichtiges Maß für die „Härte“ (Schwierigkeit oder eben Komplexität) von Problemen. Dazu ist zu sagen, dass die Zeitkomplexität eines Algorithmus niemals kleiner sein kann als die Platzkomplexität, da für das Schreiben einer Speicherzelle jeweils ein Rechenschritt benötigt wird.
Formal werden Probleme gemäß ihrer Platzkomplexität oder Zeitkomplexität in Komplexitätsklassen eingeteilt.
Siehe auch
Wikimedia Foundation.