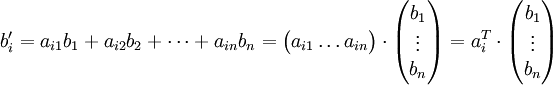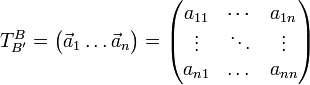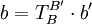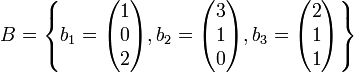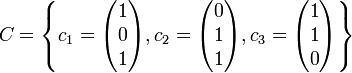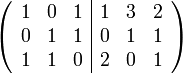- Basis-Transformation
-
Der Basiswechsel oder die Basistransformation ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums. Dadurch ändern sich im Allgemeinen die Koordinaten der Vektoren. Der Basiswechsel kann durch eine Basiswechselmatrix beschrieben werden, mit der sich auch die Koordinaten bzgl. der neuen Basis ausrechnen lassen.
Der Basiswechsel ist ein Isomorphismus und somit kann jeder Basisvektor bi' der neuen Basis B' als Linearkombination von Basisvektoren bi der ursprünglichen Basis B dargestellt werden:
Transformationsmatrix
Die Matrix des Basiswechsels, auch Transformationsmatrix zum Basiswechsel von B nach B' genannt, erhält man mit den obigen Vektoren ai als Spaltenvektoren. Man bezeichnet sie mit
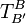 :
:Diese Matrix ist quadratisch und invertierbar. Die entsprechende inverse Matrix ist
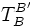 und beschreibt den Basiswechsel von B' zurück nach B. Die Transformationsmatrix
und beschreibt den Basiswechsel von B' zurück nach B. Die Transformationsmatrix 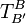 ist identisch mit der Matrix
ist identisch mit der Matrix 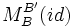 der Identitätsabbildung bei Verwendung unterschiedlicher Basen.
der Identitätsabbildung bei Verwendung unterschiedlicher Basen.Die Berechnung der Koordinaten b bzgl. der Basis B eines Vektors erfolgt durch Multiplikation der Koordinaten b' bzgl. B' mit der Transformationsmatrix
Man beachte hierbei die „Anordnung“ der Basen in der obigen Formel. Diese kehrt sich bezüglich der ursprünglichen Transformationsmatrix T um.
Beispiel
Wir betrachten zwei Basen B und C des
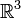 :
:wobei die Koordinatendarstellung der Vektoren die Vektoren bezüglich der Standardbasis beschreibt.
Die Abbildung eines Vektors
- v = β1b1 + β2b2 + β3b3 = γ1c1 + γ2c2 + γ3c3
ergibt sich durch die Darstellung der alten Basisvektoren (b1,b2,b3) bezüglich der neuen Basis (c1,c2,c3) und deren Gewichtung mit (β1,β2,β3).
Um die Matrix der Basistransformation
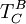 von B nach C zu berechnen, müssen wir die drei linearen Gleichungssysteme
von B nach C zu berechnen, müssen wir die drei linearen Gleichungssysteme- ci = T1ib1 + T2ib2 + T3ib3
nach den 9 Unbekannten Tji auflösen.
Dies kann mit dem Gauß-Jordan-Algorithmus für alle 3 Gleichungssysteme simultan erfolgen. Dazu wird folgendes LGS aufgestellt:
Durch Umformen mit elementaren Zeilenoperationen lässt sich die linke Seite auf die Einheitsmatrix bringen und auf der rechten Seite erhält man die Matrix
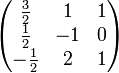 .
.
Wir betrachten einen Vektor v, der bezüglich der Standardbasis die Koordinatendarstellung (5,2,7) besitzt. Bezüglich B ist
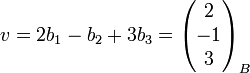 .
.
Das Subskript bezeichne die zur Koordinatendarstellung gehörige Basis. Um nun die Koordinatendarstellung bezüglich C zu berechnen, müssen wir die Transformationsmatrix auf diesen Spaltenvektor anwenden:
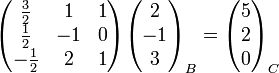 .
.
Also ist
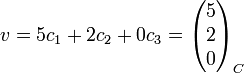 .
.
Wikimedia Foundation.