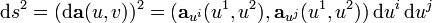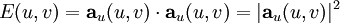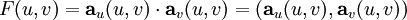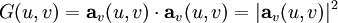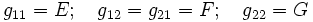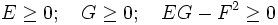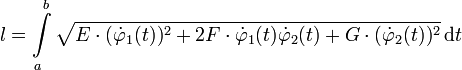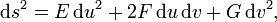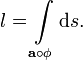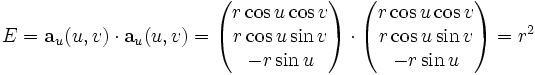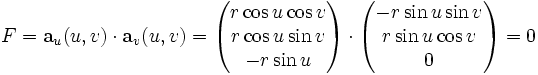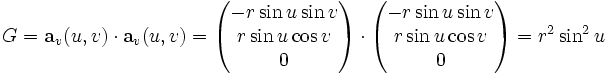- 1. Fundamentalform
-
Die erste Fundamentalform oder metrische Grundform ist ein Rechenausdruck aus der Theorie der Flächen im dreidimensionalen Raum
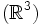 , einem Teilgebiet der klassischen Differentialgeometrie. Die erste Fundamentalform ermöglicht unter anderem die Lösung folgender Probleme:
, einem Teilgebiet der klassischen Differentialgeometrie. Die erste Fundamentalform ermöglicht unter anderem die Lösung folgender Probleme:- Berechnung der Länge einer Kurve auf der gegebenen Fläche
- Berechnung des Winkels, unter dem sich zwei Kurven auf der gegebenen Fläche schneiden
- Berechnung des Flächeninhalts eines Flächenstücks der gegebenen Fläche
Ferner lassen sich aus den Koeffizienten der ersten Fundamentalform und ihren partiellen Ableitungen die gaußsche Krümmung (Formel von Brioschi) und die Christoffelsymbole zweiter Art bestimmen (Formeln von Gauß).
Diejenigen Eigenschaften einer Fläche, die sich mit Hilfe der ersten Fundamentalform untersuchen lassen, fasst man unter der Bezeichnung innere Geometrie zusammen.
Inhaltsverzeichnis
Definition und Eigenschaften
Eine Fläche sei durch
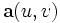 gegeben, also durch u = u1 und v = u2 parametrisiert. Wir nennen die quadratische Differentialform
gegeben, also durch u = u1 und v = u2 parametrisiert. Wir nennen die quadratische Differentialformdie erste Fundamentalform der Fläche.
Für den durch die Parameterwerte u und v bestimmten Punkt der Fläche sind die Koeffizienten der ersten Fundamentalform folgendermaßen definiert:
Dabei sind
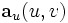 und
und 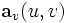 die beiden ersten partiellen Ableitungen nach den Parametern. Die Malpunkte drücken Skalarprodukte von Vektoren aus. Diese Größen nennen wir Koeffizienten der ersten Fundamentalform, weil sie Koeffizienten vor den Differentialausdrücken
die beiden ersten partiellen Ableitungen nach den Parametern. Die Malpunkte drücken Skalarprodukte von Vektoren aus. Diese Größen nennen wir Koeffizienten der ersten Fundamentalform, weil sie Koeffizienten vor den Differentialausdrücken 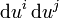 sind. Nicht zu verwechseln sind solche quadratischen Differentialformen mit den Differentialformen im Sinne von Cartan.
sind. Nicht zu verwechseln sind solche quadratischen Differentialformen mit den Differentialformen im Sinne von Cartan.Zur Vereinfachung lässt man häufig die Argumente weg und schreibt nur E, F und G für die Koeffizienten. Eine weitere (modernere) Schreibweise ist:
Die Zahlen gij sind die Koeffizienten des kovarianten metrischen Tensors.
Für die Koeffizienten der ersten Fundamentalform gilt:
Gilt zumindest EG − F2 > 0, so impliziert das auch E > 0 und G > 0 und wir nennen diese erste Fundamentalform positiv definit. Außerdem heißt eine Fläche mit positiv definiter erster Fundamentalform differentialgeometrisch regulär oder differentialgeometrisch regulär parametrisiert.
Länge einer Flächenkurve
Eine Kurve auf der gegebenen Fläche lässt sich ausdrücken durch zwei reelle Funktionen
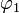 und
und 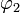 : Jedem möglichen Wert des Parameters t wird der auf der Fläche gelegene Punkt
: Jedem möglichen Wert des Parameters t wird der auf der Fläche gelegene Punkt 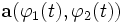 zugeordnet. Sind alle beteiligten Funktionen stetig differenzierbar, so gilt für die Länge des durch
zugeordnet. Sind alle beteiligten Funktionen stetig differenzierbar, so gilt für die Länge des durch ![t \in [a,b]](/pictures/dewiki/99/c9ef8c742260828c469822e9c5dbe2c9.png) festgelegten Kurvenstücks:
festgelegten Kurvenstücks:Den Radikanden in dieser Formel bezeichnet man als erste Fundamentalform.
Wenn wir die Schreibweise mit Differentialen verwenden:
so erhalten wir eine Rechtfertigung für die Bezeichnung Wegelement von ds2. Denn dann schreibt sich die Länge der Kurve in der Form
Inhalt eines Flächenstücks
Der Inhalt eines durch einen Parameterbereich B gegebenen Flächenstücks lässt sich berechnen durch
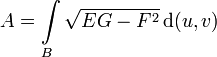 .
.
Beispiel
Die Oberfläche einer Kugel mit Radius r lässt sich parametrisieren durch
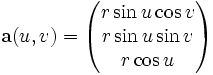 .
.
Für die Koeffizienten der ersten Fundamentalform ergibt sich:
Die erste Fundamentalform ist demnach
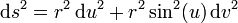 .
.
Siehe auch
Wikimedia Foundation.