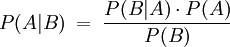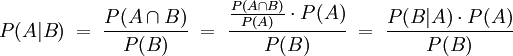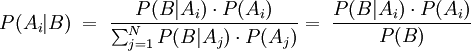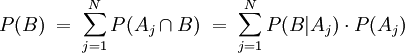- Bayes'sches Theorem
-
Das Bayestheorem (auch Satz von Bayes) ist ein Ergebnis der Wahrscheinlichkeitstheorie, benannt nach dem Mathematiker Thomas Bayes. Es gibt an, wie man mit bedingten Wahrscheinlichkeiten rechnet.
Inhaltsverzeichnis
Formel
Für zwei Ereignisse A und B mit P(B) > 0 lautet es
Hierbei ist
- P(A) die A-priori-Wahrscheinlichkeit für ein Ereignis A und
- P(B | A) die Wahrscheinlichkeit für ein Ereignis B unter der Bedingung, dass A eingetreten ist und
- P(B) die A-priori-Wahrscheinlichkeit für ein Ereignis B
Der Satz folgt unmittelbar aus der Definition der bedingten Wahrscheinlichkeit:
Bei endlich vielen Ereignissen ergibt sich das Bayessche Theorem folgendermaßen: Wenn
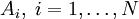 eine Zerlegung der Ergebnismenge in disjunkte Ereignisse ist, gilt für die A-posteriori-Wahrscheinlichkeit P(Ai | B)
eine Zerlegung der Ergebnismenge in disjunkte Ereignisse ist, gilt für die A-posteriori-Wahrscheinlichkeit P(Ai | B)Den zuletzt gemachten Umformungsschritt bezeichnet man auch als Marginalisierung. Man nennt diese Formel auch Bayesformel.
Die Beziehung
wird als Gesetz der totalen Wahrscheinlichkeit bezeichnet.
Interpretation
Der Satz von Bayes erlaubt in gewissem Sinn das Umkehren von Schlussfolgerungen:
Die Berechnung von P(Ereignis | Ursache) ist häufig einfach, aber oft ist eigentlich P(Ursache | Ereignis) gesucht, also ein Vertauschen der Argumente. Für das Verständnis können der Entscheidungsbaum und die A-priori-Wahrscheinlichkeit helfen. Das Verfahren ist auch als Rückwärtsinduktion bekannt.
Anwendungsgebiete
- Statistik: Alle Fragen des Lernens aus Erfahrung, bei denen eine A-priori-Wahrscheinlichkeitseinschätzung aufgrund von Erfahrungen verändert und in eine A-posteriori-Verteilung überführt wird (vgl. Bayessche Statistik).
- Medizin: Von einem oder mehreren positiven medizinischen Testergebnissen (Ereignisse, Symptome einer Krankheit) wird auf das Vorhandensein einer Krankheit (Ursache) abduktiv geschlossen.
- Informatik: Bayesscher Filter - Von charakteristischen Wörtern in einer E-Mail (Ereignis) wird auf die Eigenschaft Spam (Ursache) zu sein, geschlossen.
- Künstliche Intelligenz: Hier wird das Bayestheorem verwendet, um auch in Domänen mit "unsicherem" Wissen Schlussfolgerungen ziehen zu können. Diese sind dann nicht deduktiv und somit auch nicht immer korrekt, sondern eher abduktiver Natur, haben sich aber zur Hypothesenbildung und zum Lernen in solchen Systemen als durchaus nützlich erwiesen.
- Qualitätsmanagement: Beurteilung der Aussagekraft von Testreihen.
- Entscheidungstheorie/Informationsökonomik: Bestimmung des erwarteten Wertes von zusätzlichen Informationen.
- Grundmodell der Verkehrsverteilung.
- Bioinformatik: Bestimmung funktioneller Ähnlichkeit von Sequenzen.
- Kommunikationstheorie: Lösung von Detektions- und Dekodierproblemen.
Rechenbeispiel 1
Es sind zwei Urnen „A“ und „B“ gegeben, in denen sich rote und weiße Kugeln befinden. In „A“ sind sieben rote und drei weiße Kugeln, in „B“ eine rote und neun weiße. Es wird nun eine beliebige Kugel aus einer willkürlich gewählten Urne gezogen. Anders ausgedrückt: Ob aus Urne A oder B gezogen wird, sei a priori gleich wahrscheinlich. Es sei das Ergebnis der Ziehung: Die Kugel ist rot. Gesucht ist die Wahrscheinlichkeit dafür, dass diese rote Kugel aus Urne „A“ stammt.
Urnenversuch Es sei A das Ereignis: Die Kugel stammt aus Urne „A“. Es sei R das Ereignis „Die Kugel ist rot“. Dann gilt:
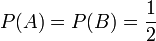 (Beide Urnen a priori gleich wahrscheinlich)
(Beide Urnen a priori gleich wahrscheinlich)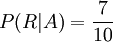 (in Urne A sind 10 Kugeln, davon 7 rote)
(in Urne A sind 10 Kugeln, davon 7 rote)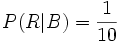 (analog)
(analog)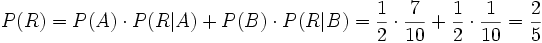 (totale Wahrscheinlichkeit)
(totale Wahrscheinlichkeit)Damit ist
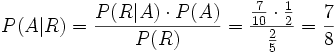 . Die Wahrscheinlichkeit, dass eine gezogene rote Kugel aus Urne „A“ stammt (A vorausgesetzt R), beträgt 7/8.
. Die Wahrscheinlichkeit, dass eine gezogene rote Kugel aus Urne „A“ stammt (A vorausgesetzt R), beträgt 7/8.Rechenbeispiel 2
In einem medizinischen Beispiel trete der Sachverhalt A, dass ein Mensch eine bestimmte Krankheit in sich trage, mit der Wahrscheinlichkeit P(A) = 0,0002 auf (Prävalenz). Jetzt soll in einem Screening-Test ermittelt werden, welche Personen diese Krankheit haben. B bezeichne die Tatsache, dass der Test bei einer Person positiv ausgefallen ist, d. h. der Test lässt vermuten, dass die Person die Krankheit hat. Der Hersteller des Tests versichert, dass der Test eine Krankheit zu 99 % erkennt (Sensitivität = P(B | A) = 0,99) und nur in 1 % der Fälle falsch anschlägt, obwohl gar keine Krankheit vorliegt (1 − Spezifität = P(B | Ac) = 0,01; wobei Ac das Komplement von A bezeichnet).
Die Frage ist: Wie wahrscheinlich ist das Vorliegen der Krankheit, wenn der Test positiv ist? (Positiver prädiktiver Wert)
Wir wissen bereits, mit welcher Wahrscheinlichkeit der Test positiv ist, wenn die Krankheit vorliegt (nämlich mit 99%-iger Wahrscheinlichkeit), jetzt soll das Ganze von der anderen Seite her gesehen werden.
Die Aufgabe kann
- durch Einsetzen in die Formel oder
- durch einen Entscheidungsbaum (nur bei diskreten Wahrscheinlichkeiten)
gelöst werden.
Lösung mit dem Satz von Bayes
Da P(B) unbekannt ist, muss man P(B) auf die bekannten Größen zurückführen. Dies geschieht mittels folgender Gleichungskette:
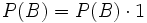
-
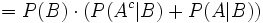
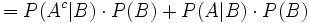
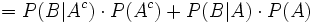 (Satz von Bayes)
(Satz von Bayes)
Nach dieser Umformung kann nun der Satz von Bayes auf die gegebenen Daten angewendet werden
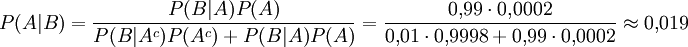
Es liegt also nur zu 1,9 % eine Krankheit vor d. h. der Patient hat eine Chance von 98 % gesund zu sein, obwohl der Test ihn als krank einschätzte! Das ist schwer zu glauben, liegt aber daran, dass die Wahrscheinlichkeit tatsächlich erkrankt zu sein (0,02 %) um das fünfzigfache geringer ist als die Wahrscheinlichkeit eines falschen Testergebnisses (1 %). Diese Problematik und dessen Konsequenzen werden von Gerd Gigerenzer im Buch Das Einmaleins der Skepsis ausführlich beschrieben.
Lösung mittels Baumdiagramm
Probleme mit wenigen Klassen und einfachen Verteilungen lassen sich übersichtlich im Baumdiagramm für die Aufteilung der Häufigkeiten darstellen. Geht man von den Häufigkeiten auf relative Häufigkeiten bzw. auf (bedingte) Wahrscheinlichkeiten über, wird aus dem Baumdiagramm ein Ereignisbaum, ein Sonderfall des Entscheidungsbaums.
10 000 / \ / \ / \ 2(krank) 9 998 (gesund) /\ /\ / \ / \ / \ / \ / \ / \ Test- 0 2 100 9898 ergebnis - + + - (gerundet)Ergebnis: 2+100=102 haben ein positives Ergebnis, obwohl 100 (=falsch positiv) von ihnen gesund sind. Diese Angaben erfolgen hier in der absoluten Häufigkeit.
Parameterschätzung mit dem Bayestheorem
Ermittlung von Messunsicherheiten
Für die Ermittlung von Unsicherheiten beim Messen existiert der international vereinbarte Leitfaden GUM (Norm). Eine der empfohlenen Methoden zur Bestimmung der Messunsicherheit basiert auf der Formel von Bayes und funktioniert im Kern folgendermaßen: Zu bestimmen ist ein Parameter α, der einer Messung direkt nicht zugänglich ist. Messbar ist die Zufallsvariable X, deren Verteilungsdichte f vom Parameter α abhängt: fα(x).
Der Parameter α wird als Realisierung einer Zufallsvariablen Α aufgefasst. Das anfängliche Wissen oder auch Unwissen hinsichtlich dieser Variablen wird durch die A-priori-Verteilungsdichte g(α) modelliert. Die A-priori-Wahrscheinlichkeitsdichte kann das Ergebnis vergangener Beobachtungen sein oder sie kann nach dem Prinzip maximaler Unwissenheit als nichtinformative Verteilung angesetzt werden (Rüger, 1999, S. 211 ff.).
Wird nun ein bestimmter Wert x gemessen, dann ergibt sich mit der Formel von Bayes eine neue Schätzung der Verteilungsdichte des Parameters, die A-posteriori-Schätzung h(α):
- h(α) ~ fα(x)∙g(α).
Hierin ist der Proportionalitätsfaktor durch die Eigenschaft der Dichte bestimmt: Das Integral über h muss den Wert 1 ergeben.
Die A-posteriori-Schätzung kann laut Messunsicherheits-Leitfaden GUM als Verbesserung der ursprünglichen Schätzung angesehen werden.
Kritik
Anders als bei den klassischen Test- und Schätzverfahren (Beispiel: Konfidenzintervall) gibt es für die Bayes-Schätzung von Messunsicherheiten keine gesicherten Genauigkeitsangaben. Zuweilen ergeben mehr Daten sogar schlechtere Folgerungen[1]. Dass es zu solchen paradoxen Resultaten kommen kann, liegt daran, dass die Bayes-Schätzung von Parametern nicht auf einer logisch zwingenden Deduktion beruht.
Wenn man die A-posteriori-Verteilung des Parameters als eine gegenüber der A-priori-Verteilung bessere Schätzung der tatsächlichen Verteilung des Parameters ansieht, dann ist das lediglich ein plausibler Schluss. Die A-posteriori-Verteilung ist nur eine verbesserte Schätzung unter der Bedingung des Messergebnisses; sie besagt, mit welchen Wahrscheinlichkeiten die verschiedenen Parameterwerte zu dem beobachteten Messergebnis beigetragen haben können. Der Umkehrschluss von der Beobachtung auf die tatsächliche Verteilung des Parameters kann demnach auch falsch sein. Denn im Grunde werden „aus einer Beobachtung zu starke Schlussfolgerungen gezogen”[2], ein altbekanntes Problem der Induktion, auf das bereits David Hume und Karl Raimund Popper hingewiesen haben.
Eine umfassende Behandlung der mit der Parameterschätzung einhergehenden Probleme bietet die Test- und Schätztheorie (Rüger, 1999).
Siehe auch
Weblinks
- Thomas Bayes: Original-Text (1763): "An Essay towards solving a Problem in the Doctrine of Chances" (PDF)
- Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Rudolf Sponsel: Das Bayes'sche Theorem
- Der Bayessche Satz der Wahrscheinlichkeit
- Ian Stewart: The Interrogator's Fallacy (Ein Anwendungsbeispiel aus der Kriminalistik (Englisch))
- Christoph Wassner, Stefan Krauss, Laura Martignon: Muss der Satz von Bayes schwer verständlich sein? (Ein Artikel zur Mathematikdidaktik.)
- Gerechnete Übungsbeispiele
- Sammlung der Denkfallen und Paradoxa von Timm Grams
Literaturhinweise
Rüger, Bernhard: Test- und Schätztheorie. Band I: Grundlagen. Oldenbourg, München 1999
Wikimedia Foundation.