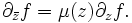Laplace-Beltrami-Operator — Der Laplace Operator Δ ist ein mathematischer Operator (also eine Rechenvorschrift), der zuerst von Pierre Simon Laplace eingeführt wurde. Er spielt in vielen physikalischen Theorien, insbesondere bei der Beschreibung elektrischer und… … Deutsch Wikipedia
Dolbeault-Operator — Die äußere Ableitung oder Cartan Ableitung ist eine Funktion aus den Bereichen Differentialgeometrie und Analysis. Die äußere Ableitung verallgemeinert das aus der Analysis bekannte Leibniz sche Differential auf den Raum der Differentialformen.… … Deutsch Wikipedia
Äußere Ableitung — Die äußere Ableitung oder Cartan Ableitung ist eine Funktion aus den Bereichen Differentialgeometrie und Analysis. Die äußere Ableitung verallgemeinert das aus der Analysis bekannte Leibniz sche Differential auf den Raum der Differentialformen.… … Deutsch Wikipedia
Quasikonforme Abbildung — In der Funktionentheorie ist eine quasikonforme Abbildung eine Verallgemeinerung einer biholomorphen Abbildung. Hier wird im Wesentlichen auf die Winkeltreue verzichtet. Inhaltsverzeichnis 1 Definition 2 Beltrami Gleichung 3 Hauptsatz … Deutsch Wikipedia
Komplexe Geometrie — Komplexe Mannigfaltigkeiten sind topologische Mannigfaltigkeiten, deren Kartenwechselhomöomorphismen sogar konform sind. Diese Objekte werden in der Differentialgeometrie und der Funktionentheorie untersucht. Ihre Definition ist analog zu der… … Deutsch Wikipedia
Komplexe Struktur — Komplexe Mannigfaltigkeiten sind topologische Mannigfaltigkeiten, deren Kartenwechselhomöomorphismen sogar konform sind. Diese Objekte werden in der Differentialgeometrie und der Funktionentheorie untersucht. Ihre Definition ist analog zu der… … Deutsch Wikipedia
Komplexe Mannigfaltigkeit — Komplexe Mannigfaltigkeiten sind topologische Mannigfaltigkeiten, deren Kartenwechselhomöomorphismen sogar konform sind. Diese Objekte werden in der Differentialgeometrie und der Funktionentheorie untersucht. Ihre Definition ist analog zu der… … Deutsch Wikipedia
Delta-Operator — Der Laplace Operator Δ ist ein mathematischer Operator (also eine Rechenvorschrift), der zuerst von Pierre Simon Laplace eingeführt wurde. Er spielt in vielen physikalischen Theorien, insbesondere bei der Beschreibung elektrischer und… … Deutsch Wikipedia
Deltaoperator — Der Laplace Operator Δ ist ein mathematischer Operator (also eine Rechenvorschrift), der zuerst von Pierre Simon Laplace eingeführt wurde. Er spielt in vielen physikalischen Theorien, insbesondere bei der Beschreibung elektrischer und… … Deutsch Wikipedia
Laplaceoperator — Der Laplace Operator Δ ist ein mathematischer Operator (also eine Rechenvorschrift), der zuerst von Pierre Simon Laplace eingeführt wurde. Er spielt in vielen physikalischen Theorien, insbesondere bei der Beschreibung elektrischer und… … Deutsch Wikipedia
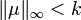 ist.
ist.