- ABCD-Matrix
-
Die Matrizenoptik ist eine Rechenmethode in der geometrischen Optik, bei der die Veränderung von Lichtstrahlen durch optische Bauelemente mit Hilfe von Matrizen bestimmt wird. Diese nennt man (Strahl-)Transfermatrizen oder auch, nach ihren vier Einträgen, ABCD-Matrizen.
Inhaltsverzeichnis
Grundlagen
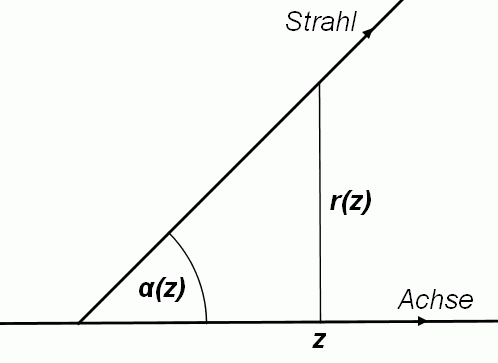
Man betrachtet die Lichtausbreitung entlang der optischen Achse, üblicherweise als z-Achse definiert. Für die Zwecke der geometrischen Optik kann der Zustand eines Lichtstrahles an einem Punkt (also bei einem bestimmten z) durch zwei Werte beschrieben werden: seinen Abstand r zur optischen Achse und den Winkel α, den er mit ihr einschließt. Man kann den Strahl also mit einem z-abhängigen Vektor aus diesen beiden Komponenten darstellen:
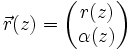
Der Winkel α gibt dabei, da er die Neigung des Strahls darstellt, die Änderung von r mit z an. Im Rahmen der paraxialen Näherung, sprich mit nur geringen Abständen r zur optischen Achse und kleinen Neigungen α, gilt
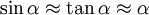 . Somit besteht zwischen zwei Zustandsvektoren
. Somit besteht zwischen zwei Zustandsvektoren 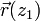 ,
, 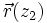 desselben Strahls bei verschiedenen z-Werten ein linearer Zusammenhang, der mit einer Matrix beschrieben werden kann. Man multipliziert dazu die durch die Eigenschaften eines optischen Elementes bestimmte Transformationsmatrix an den ersten Vektor und erhält den zweiten, also die Eigenschaften des Strahles nach Durchgang durch das Element:
desselben Strahls bei verschiedenen z-Werten ein linearer Zusammenhang, der mit einer Matrix beschrieben werden kann. Man multipliziert dazu die durch die Eigenschaften eines optischen Elementes bestimmte Transformationsmatrix an den ersten Vektor und erhält den zweiten, also die Eigenschaften des Strahles nach Durchgang durch das Element: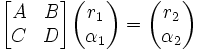
Die übliche Konvention ist, dass die Strahlrichtung (also die positive z-Achse) von links nach rechts verläuft. r wird oberhalb der Achse positiv, unterhalb negativ gezählt. α ist positiv, wenn der Strahl nach oben zeigt, und negativ, wenn der Strahl nach unten zeigt.
Transfermatrizen wichtiger Elemente
Translation
Breitet sich ein Lichtstrahl ungehindert über die Distanz d entlang der optischen Achse aus, wird dies mit der folgenden Matrix des optischen Weges beschrieben:
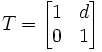
Die Translationsmatrix ist unabhängig von dem Medium, durch das der Strahl propagiert. Es folgt der Vektor:
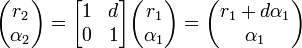
Ein sich einfach ausbreitender Strahl ändert also seine Neigung zur Achse nicht, sondern nur gemäß seiner Anfangsneigung seinen Abstand zu ihr.
Brechung an ebener Fläche
Wird ein Strahl an einer ebenen Fläche gebrochen, lautet die Transfermatrix gemäß dem Brechungsgesetz wie folgt:
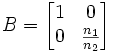 ,
,wobei
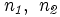 der Brechzahl der optischen Medien vor und nach der Grenzfläche entsprechen.
der Brechzahl der optischen Medien vor und nach der Grenzfläche entsprechen.Brechung an gekrümmter Fläche
Wird ein Lichtstrahl an einer gekrümmten Fläche gebrochen, so lautet die Transfermatrix
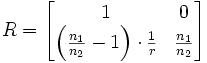 ,
,wobei r der Krümmungsradius und
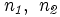 wiederum die Brechzahlen der optischen Medien vor und nach der Grenzfläche sind.
wiederum die Brechzahlen der optischen Medien vor und nach der Grenzfläche sind.Dünne Linse
Aus der Linsengleichung oder durch Multiplikation zweier Kugelflächen-Brechungsmatrizen erhält man für den Durchgang durch eine dünne Linse
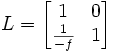 ,
,wobei f der Brennweite der Linse entspricht. f ist größer 0, wenn die Linse fokussierend wirkt, f ist kleiner 0, wenn die Linse defokussierend wirkt.
Ebener Spiegel
Für den ebenen Spiegel erhält man
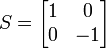
Sphärischer Spiegel
Für sphärische Spiegel (Kugelspiegel) erhält man
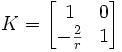
Der Radius r des Spiegels ist für konkave Spiegel positiv, für konvexe Spiegel negativ.
Kombination von Elementen
Durchläuft ein Strahl mehrere optische Elemente hintereinander, so werden nacheinander die entsprechenden Transfermatrizen auf den Strahlvektor angewandt, was äquivalent dazu ist, sie zu multiplizieren und dann die Produktmatrix auf den Vektor anzuwenden. Dabei gelten die Regeln der Matrizenmultiplikation: durchläuft der Strahl drei Elemente in der Reihenfolge T1,T2,T3, so wird das Produkt in der Reihenfolge
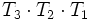 geschrieben und in der Reihenfolge
geschrieben und in der Reihenfolge 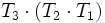 ausmultipliziert.
ausmultipliziert.So ergeben sich die Matrizen komplizierterer Bauteile aus den elementaren, etwa die einer dicken Linse aus denen einer gekrümmten Grenzfläche, einer Translation durch das Linsenglas und einer gegenläufig gekrümmten Grenzfläche; oder die eines Linsensystems aus Linse, Translation, Linse.
Alternative Konvention
Von einigen Autoren wird abweichend zur hier verwendeten Konvention der Strahlvektor definiert als
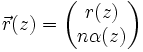 , wobei n die Brechzahl des Mediums am Ort (r,z) ist. Dies hat zur Folge, dass etwa in der Matrix für Translation durch ein Medium für dieses zusätzliche n korrigiert werden muss, sie lautet in dieser Konvention
, wobei n die Brechzahl des Mediums am Ort (r,z) ist. Dies hat zur Folge, dass etwa in der Matrix für Translation durch ein Medium für dieses zusätzliche n korrigiert werden muss, sie lautet in dieser Konvention 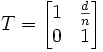 und ist somit selbst explizit vom Medium abhängig.
und ist somit selbst explizit vom Medium abhängig.Weitere Anwendungen
Gaußstrahlen
Die Anwendung der Matrizenoptik ist nicht auf die geometrische Optik beschränkt, sie lässt sich auch auf das Konzept der Gaußstrahlen übertragen. Hierzu bleiben die ABCD-Matrizen und ihre Multiplikationsregeln komplett erhalten, man wendet sie aber nicht mehr per Multiplikation auf einen Strahlvektor an, sondern auf den Strahlparameter q gemäß folgender Vorschrift:
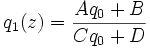 .
.
Der Strahlparameter berechnet sich hierbei nach
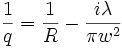 mit R dem Krümmungsradius des Gaußschen Strahls, λ der Wellenlänge und 2w dem Strahldurchmesser.
mit R dem Krümmungsradius des Gaußschen Strahls, λ der Wellenlänge und 2w dem Strahldurchmesser.Polarisation
Ein zur geometrischen Matrizenoptik analoges Verfahren wird verwendet, um die Veränderung der Polarisation beim Durchgang durch optische Elemente zu berechnen. Der Polarisationszustand wird durch Jones-Vektoren ausgedrückt und mit Jones-Matrizen manipuliert.
Literatur
- D. Meschede: Optik, Licht und Laser. B.G. Teubner; Stuttgart, Leipzig ISBN 3-5191-3248-6
- F. Pedrotti, L. Pedrotti, Werner Bausch, Harmut Schmidt: Optik. Prentice Hall; München, London, Mexiko, New York, Singapur, Sydney, Toronto, ISBN 3-8272-9510-6
Weblinks
- Grundlagen der paraxialen Matrizen-Optik, Dr. Harm Fesefeldt, RWTH Aachen
Wikimedia Foundation.