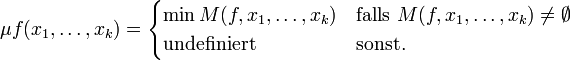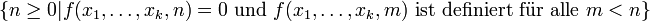- Μ-rekursive Funktion
-
Die Klasse Pr der μ-rekursiven Funktionen oder partiell-rekursiven Funktionen spielt in der Rekursionstheorie, einem Teilgebiet der theoretischen Informatik, eine wichtige Rolle. Sie beschreibt die Menge aller Funktionen, die im intuitiven Sinn berechenbar sind. Eine wichtige echte Teilmenge der μ-rekursiven Funktionen sind die primitiv-rekursiven Funktionen.Die Klasse der μ-rekursiven Funktionen stimmt überein mit der Klasse der Turing-berechenbaren Funktionen. Es stellt sich heraus, dass die unterschiedlichen entwickelten Berechenbarkeitsbegriffe (μ-rekursive Funktionen, Lambda-Kalkül, Turingmaschinen, Registermaschinen, WHILE-Programme etc.) übereinstimmen und den intuitiven Begriff der Berechenbarkeit vollständig erfassen (Churchsche These).
Die primitiv-rekursiven Funktionen sind aus einfachen Grundfunktionen (konstante 0-Funktion, Projektionen auf ein Argument und Nachfolgerfunktion) durch Komposition und primitive Rekursion aufgebaut. Dadurch erhält man immer totale Funktionen, also Funktionen im eigentlichen Sinn. Die μ-rekursiven Funktionen sind demgegenüber partielle Funktionen, die aus denselben Konstrukten und zusätzlich durch die Anwendung des μ-Operators gebildet werden können. Durch die Anwendung des μ-Operators wird Partialität eingeführt.
Inhaltsverzeichnis
Definition des μ-Operators
Für eine partielle Funktion
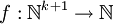 ist die partielle Funktion
ist die partielle Funktion 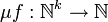 definiert durch:
definiert durch:wobei die Menge
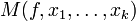 definiert ist als
definiert ist alsInsbesondere bildet der Operator μ eine (k + 1)-stellige partielle Funktion auf eine k-stellige partielle Funktion ab.
Das Programm μf kann verstanden werden als eine While-Schleife, die nach oben zählt, und die deswegen nicht terminieren muss:
Parameter: x1,...,xk. Setze n auf 0; Solange
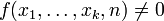 erhöhe n um Eins;
Ergebnis: n.
erhöhe n um Eins;
Ergebnis: n.
Definition der μ-rekursiven Funktionen
Die Klasse Pr der μ-rekursiven Funktionen (von
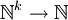 ) umfasst die folgenden Grundfunktionen:
) umfasst die folgenden Grundfunktionen:- konstante 0-Funktion:
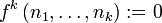
- Projektion auf ein Argument:
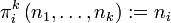 ,
, 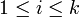
- Nachfolgefunktion:
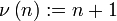
Die μ-rekursiven Funktionen erhält man als Abschluss der Grundfunktionen bezüglich der drei folgenden Operationen:
- Die Komposition:
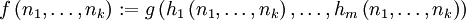 , falls
, falls 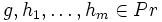
- Die Primitive Rekursion:
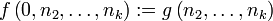 und
und 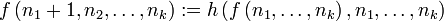 , falls
, falls 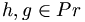
- Der μ-Operator.
Äquivalenz der μ-rekursiven Funktionen mit der Turingmaschine
Es lässt sich beweisen, dass eine Turingmaschine (TM) durch μ-rekursive Funktionen simuliert werden kann. Es lässt sich auch beweisen, dass die Menge der μ-rekursiven Funktionen genau der Menge der Turing-berechenbaren Funktionen entspricht.
Beweis-Skizze für die Simulation der TM mit μ-rekursiven Funktionen
Man kann zeigen, dass sich die Konfiguration einer TM durch drei Zahlen a, b, c darstellen lässt. Genau so kann eine Funktion h(a,b,c) = y (eine bijektive Abbildung
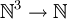 ) definiert werden, die eine geeignete Kodierung der TM ist.
) definiert werden, die eine geeignete Kodierung der TM ist.Nehmen wir also eine primitiv-rekursive Funktion
- f(n,x) = y,
die eine geeignete Kodierung der TM liefert für die Eingabe x nach n Berechnungsschritten,
und eine zweite primitiv-rekursive Funktion
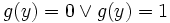 ,
,
die für eine Kodierung y als Ergebnis 0 liefert, falls y einen Endzustand der TM repräsentiert, und ansonsten 1.
Dann ergibt
- Anzahl(x) = μ(g(f(n,x)))
die Anzahl der Schritte, die eine TM zur Berechnung bis zum Ende benötigt. Also bekommen wir mit
- Berechnung(x) = f(Anzahl(x),x)
die Berechnung der TM in einem Endzustand bei der Eingabe x.
Bemerkung
- Die Berechenbarkeit einer μ-rekursiven Funktion bezieht sich auf Werte aus ihrem Definitionsbereich. Es existiert kein allgemeines Verfahren, das alle Werte liefert, die nicht zum Definitionsbereich einer μ-rekursiven Funktion gehören.
- Der μ-Operator realisiert einen Suchprozess, der genau dann abbricht, wenn der gesuchte Wert existiert.
Beispiele
- Alle primitiv rekursiven Funktionen sind μ-rekursiv.
- Die Ackermannfunktion und die Sudanfunktion sind totale μ-rekursive Funktionen.
- Die Funktion Fleißiger Biber (busy beaver) ist nicht μ-rekursiv.
- Die Folge der Ziffern der Halte-Wahrscheinlichkeit (Chaitinsche Konstante Ω) ist nicht μ-rekursiv. Die Halte-Wahrscheinlichkeit ist definiert durch
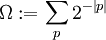 , wobei p ein haltendes Programm ist und
, wobei p ein haltendes Programm ist und 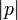 die Länge des Programms in Bit bezeichnet.
die Länge des Programms in Bit bezeichnet.
Literatur
- H.-D. Ebbinghaus, J. Flum, W. Thomas: Einführung in die mathematische Logik. Spektrum, Akad. Verl., Heidelberg, Berlin 1996.
- A. Oberschelp: Rekursionstheorie. BI-Wiss.-Verl., Mannheim, Leipzig, Wien, Zürich 1993.
Wikimedia Foundation.