- Berechenbare Funktion
-
In der Berechenbarkeitstheorie nennt man eine Funktion berechenbar, wenn es einen Algorithmus gibt, der die Funktion berechnet. Die Funktion, die ein Algorithmus berechnet, ist gegeben durch die Ausgabe, mit der der Algorithmus auf eine Eingabe reagiert. Der Definitionsbereich der Funktion ist die Menge der Eingaben, für die der Algorithmus überhaupt eine Ausgabe produziert. Wenn der Algorithmus nicht terminiert, dann liegt die Eingabe nicht im Definitionsbereich.
Dem Algorithmusbegriff liegt ein Berechnungsmodell zugrunde. Verschiedene Berechnungsmodelle sind entwickelt worden, es hat sich aber herausgestellt, dass die stärksten davon zum Modell der Turingmaschine gleich stark (Turing-mächtig) sind. Die Church-Turing-These behauptet daher, dass die Turingmaschinen den intuitiven Begriff der Berechenbarkeit wiedergeben.
Zu den Berechnungsmodellen, die schwächer sind als Turingmaschinen, gehören zum Beispiel die Loop-Programme. Diese können zum Beispiel die Turing-berechenbare Ackermann-Funktion nicht berechnen.
Ein dem Begriff der Berechenbarkeit eng verwandter Begriff ist der der Entscheidbarkeit. Eine Teilmenge einer Menge (zum Beispiel eine Formale Sprache) heißt entscheidbar, wenn ihre charakteristische Funktion (im Wesentlichen das zugehörige Prädikat) berechenbar ist.
Inhaltsverzeichnis
Formale Definition
Man sagt, der Algorithmus P berechnet die Funktion
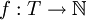 mit
mit 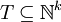 , wenn P bei Eingabe von
, wenn P bei Eingabe von 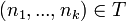 nach einer endlichen Zahl von Schritten den Wert
nach einer endlichen Zahl von Schritten den Wert 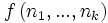 ausgibt, und bei Eingabe von
ausgibt, und bei Eingabe von 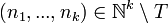 nicht terminiert.
nicht terminiert.Eine Funktion heißt berechenbar, wenn es einen Algorithmus gibt, der sie berechnet.
Den Berechenbarkeitsbegriff kann man gleichwertig auf partielle Funktionen übertragen. Eine partielle Funktion
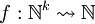 heißt berechenbar, wenn sie eingeschränkt auf ihren Definitionsbereich
heißt berechenbar, wenn sie eingeschränkt auf ihren Definitionsbereich 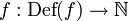 eine berechenbare Funktion ist.
eine berechenbare Funktion ist.Zahlenfunktionen
Definition berechenbarer Funktionen mit Registermaschinen
Eine Funktion
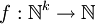 ist berechenbar genau dann, wenn es eine k-stellige Registermaschine M gibt, deren Maschinenfunktion mit f übereinstimmt, also f = fM gilt.
ist berechenbar genau dann, wenn es eine k-stellige Registermaschine M gibt, deren Maschinenfunktion mit f übereinstimmt, also f = fM gilt.Z. B. ist die Funktion
- f(x) = div
(die für kein Argument terminiert) berechenbar, da es eine entsprechende Registermaschine gibt.
Definition mit WHILE-Programmen
Eine Funktion f (wie oben) ist berechenbar genau dann, wenn es ein WHILE-Programm P gibt, mit
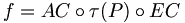 .
.
Dabei ist EC die Eingabecodierung, AC die Ausgabecodierung und τ(P) die von P über die Semantik realisierte Maschinenfunktion.
Definition durch Rekursion
Seien μ, Sub und Prk die Operationen der µ-Rekursion, der Substitution und primitiven Rekursion. Funktionen, die sich aus der Menge der primitiv-rekursiven Grundfunktionen durch wiederholtes Anwenden dieser Operatoren erzeugen lassen, heißen µ-rekursiv. Die Menge der μ-rekursiven Funktionen ist genau die Menge der berechenbaren Funktionen.
Übergang von einstelligen zu mehrstelligen Funktionen
Über die cantorsche Paarungsfunktion führt man den Begriff der Berechenbarkeit einer k-stelligen Funktion auf den der Berechenbarkeit von einstelligen Funktionen zurück. Insbesondere kann man damit in natürlicher Weise definieren, welche Funktionen auf den rationalen Zahlen berechenbar sind.
Wortfunktionen
Die Berechenbarkeit von Wortfunktionen lässt sich entweder mit Hilfe von Turingmaschinen zeigen. Alternativ führt man eine Standardnummerierung über die Wörter über Σ * ein und zeigt, dass die so erzeugten Zahlenfunktionen berechenbar sind.
Uniforme Berechenbarkeit
Eine zweistellige Funktion f(x,y) mit der Eigenschaft, dass für jeden festen Wert a die durch fa(y) = f(a,y) definierte einstellige Funktion fa berechenbar ist, muss selbst nicht unbedingt berechenbar sein; für jeden Wert a gibt es zwar einen Algorithmus (also etwa eine programm für eine Turingmaschine) Ta, der fa berechnet, aber die Abbildung a → Ta ist im Allgemeinen nicht berechenbar.
Eine Familie (fa: a=0,1,2,...) von berechenbaren Funktionen heißt uniform berechenbar, wenn es einen Algorithmus gibt, der zu jedem a einen Algorithmus Ta liefert, welcher fa berechnet. Man kann leicht zeigen, dass so eine Familie genau dann uniform berechenbar ist, wenn die zweistellige Funktion (x, y) → fx(y) berechenbar ist.
Eigenschaften
- Die Komposition von berechenbaren Funktionen ist berechenbar.
- Der Definitionsbereich einer berechenbaren Funktion ist rekursiv aufzählbar.
- Der Wertebereich einer berechenbaren Funktion ist rekursiv aufzählbar.
- Die universelle Funktion nimmt seinen ersten Parameter als Gödelnummer eines Algorithmus und wendet diesen Algorithmus an auf seinen zweiten Parameter. Die universelle Funktion ist berechenbar zum Beispiel durch eine universelle Turingmaschine.
Siehe auch
Wikimedia Foundation.
