- Bessel'sche Ungleichung
-
Die besselsche Ungleichung (nach Friedrich Wilhelm Bessel) beschreibt in der Funktionalanalysis den Sachverhalt, dass ein Vektor f eines Hilbertraums mindestens so "lang" ist, wie eine (beliebige) seiner Projektionen auf Unterräume.
Ist also H ein Hilbertraum und
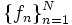 ein Orthonormalsystem in H. Dann gilt für alle
ein Orthonormalsystem in H. Dann gilt für alle 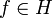 die Ungleichung
die Ungleichung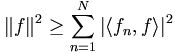 ,
,
wobei
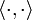 das Skalarprodukt auf dem Hilbertraum darstellt.
das Skalarprodukt auf dem Hilbertraum darstellt.Gilt in der besselschen Ungleichung das Gleichheitszeichen, so heißt sie parsevalsche Gleichung und stellt eine Verallgemeinerung des Satzes des Pythagoras für Innenprodukträume dar.
Wikimedia Foundation.
