- Beta-Fehler
-
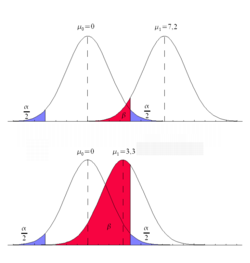 Darstellung möglicher Werte der Wahrscheinlichkeit für einen Fehler 2. Art (rot) am Beispiel eines Signifikanztests für einen Parameter μ. Der Fehler 2. Art ist vom Wert des wahren Parameters μ abhängig. Je dichter dieser bei dem unter der Nullhypothese angenommen Wert liegt, desto größer ist die Wahrscheinlichkeit für einen Fehler 2. Art. Da der wahre Wert von μ bei Annahme der Alternativhypothese nicht bekannt ist, kann die Wahrscheinlichkeit für den Fehler zweiter Art im Gegensatz zum Fehler 1. Art (blau) nicht berechnet werden.
Darstellung möglicher Werte der Wahrscheinlichkeit für einen Fehler 2. Art (rot) am Beispiel eines Signifikanztests für einen Parameter μ. Der Fehler 2. Art ist vom Wert des wahren Parameters μ abhängig. Je dichter dieser bei dem unter der Nullhypothese angenommen Wert liegt, desto größer ist die Wahrscheinlichkeit für einen Fehler 2. Art. Da der wahre Wert von μ bei Annahme der Alternativhypothese nicht bekannt ist, kann die Wahrscheinlichkeit für den Fehler zweiter Art im Gegensatz zum Fehler 1. Art (blau) nicht berechnet werden.Als Fehler 2. Art wird beim statistischen Testen der Fehler bezeichnet, den man begeht, wenn man die Nullhypothese beibehält, obwohl die Alternativhypothese gilt. Alternative Bezeichnungen sind β-Fehler (Beta-Fehler) und Falsch-negativ-Entscheidung. Im Gegensatz zum Fehler 1. Art, der eintritt, wenn die Null-Hypothese fälschlicherweise abgelehnt wird, lässt sich die Wahrscheinlichkeit für den Fehler 2. Art meist nicht berechnen. Dies hat seinen Grund in der Art der Festlegung der Hypothesen eines statistischen Tests. Während die Null-Hypothese stets eine dezidierte Aussage wie beispielsweise H0: „ Mittelwert μ = 0 “ darstellt, ist die Alternativhypothese, da sie ja alle sonstigen Möglichkeiten erfasst, meist globaler Natur (bspw. H1: „ Mittelwert μ ≠ 0 “ ). Die rechtsstehende Graphik illustriert die Wahrscheinlichkeit des Fehlers 2. Art (rot) in Abhängigkeit vom unbekannten Mittelwert μ.
Inhaltsverzeichnis
Entscheidungstabelle
Wahrer Sachverhalt: H0
(Es gibt keinen Unterschied)Wahrer Sachverhalt: H1
(Es gibt einen Unterschied)durch einen statistischen Test fällt eine Entscheidung für: H0 richtige Entscheidung (Spezifität)
Wahrscheinlichkeit: 1-αFehler 2. Art
Wahrscheinlichkeit: βdurch einen statistischen Test fällt eine Entscheidung für: H1 Fehler 1. Art
Wahrscheinlichkeit: αrichtige Entscheidung
Wahrscheinlichkeit: 1-β ("Power", Sensitivität)Beispiele
- Ein Tester hat eine Urne vor sich, in die er nicht hineinschauen kann. Darin befinden sich rote und grüne Kugeln. Es kann jeweils nur eine Kugel zu Testzwecken aus der Urne entnommen werden.
- Alternativhypothese: „In der Urne befinden sich mehr rote als grüne Kugeln“.
- Um ein Urteil über den Inhalt der Urne abgeben zu können, wird der Tester der Urne mehrmals Kugeln zu Testzwecken entnehmen. Die Nullhypothese in unserem Beispiel lautet, dass entweder genauso viele rote wie grüne, oder aber mehr grüne als rote Kugeln in der Urne sind (das Gegenteil der Alternativhypothese). Wenn der Tester aufgrund seiner Stichprobe also zu dem Schluss kommt, die Nullhypothese sei richtig bzw. die Alternativhypothese falsch, obwohl in Wahrheit doch die Alternativhypothese richtig ist, dann beginge er einen Fehler 2. Art.
- Wir möchten den Einfluss der Ernährung auf die geistige Entwicklung von Kindern in Kinderheimen untersuchen. Dafür vergleichen wir zwei Gruppen von Kindern hinsichtlich ihrer Leistung in kognitiven Tests: Die eine Stichprobe wird nach dem herkömmlichen Plan ernährt, die andere erhält eine besonders gesunde Kost. Wir vermuten, dass die gesunde Kost sich positiv auf die kognitiven Leistungen auswirkt.
- Alternativhypothese: „Kinder, die eine besonders gesunde Kost erhalten, weisen bessere kognitive Leistung auf als Kinder, die auf die herkömmliche Weise ernährt werden.“
- Wenn wir nun die kognitive Leistung unserer beiden Stichproben vergleichen, so stellen wir keinen Unterschied in der kognitiven Leistung fest. Demzufolge halten wir die Alternativhypothese für falsch und bestätigen die Nullhypothese. Wenn jedoch in Wahrheit die Population der gesund Ernährten doch eine bessere Leistung aufweist, dann begehen wir einen Fehler 2. Art.
- Aber wir haben in unserer Stichprobe doch keinen Unterschied festgestellt? Diese Gleichheit kann aber auch auf die zufällige Streuung der Messergebnisse oder auf die ungünstige Zusammenstellung unserer Stichproben zurückzuführen sein.
- Das Begehen eines Fehlers 2. Art ist in der Regel weniger „schlimm“, als ein Fehler 1. Art. Dies hängt jedoch individuell vom Untersuchungsgegenstand ab. In unserem Beispiel hat der Fehler 2. Art sehr negative Konsequenzen: Obwohl die gesunde Ernährung die Leistung verbessert, entscheiden wir uns, die herkömmliche Ernährung beizubehalten. Ein Fehler 1. Art, also die Einführung der gesunden Ernährung für alle Kinder, obwohl diese keine Leistungsverbesserung bringt, scheint hier weniger fatale Konsequenzen zu haben.
Hinweis: Bei der Berechnung mit Beta (und auch Alpha) handelt es sich um bedingte Wahrscheinlichkeiten.Siehe auch
Weblinks
Wikimedia Foundation.
