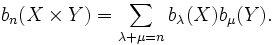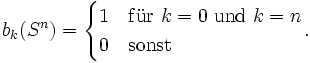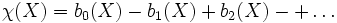Bettische Zahlen

Im mathematischen Teilgebiet der Topologie sind die Bettizahlen (nach E. Betti) eine Folge nichtnegativer ganzer Zahlen, die globale Eigenschaften eines topologischen Raumes beschreiben. Sie sind topologische Invarianten.

Definition

Es sei X ein topologischer Raum. Dann ist die i-te Bettizahl von X

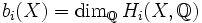$b_i(X) = \dim_{\mathbb Q}H_i(X,\mathbb Q)$ für $i=0,1,2,\ldots$

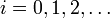
Dabei bezeichnet 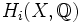$H_i(X,\mathbb Q)$ die i-te singuläre Homologiegruppe mit Koeffizienten in den rationalen Zahlen.

Eigenschaften

• b₀(X) ist die Anzahl der Zusammenhangskomponenten von X.
• b₁(X) ist der Rang der abelsch gemachten Fundamentalgruppe von X.
• Für eine orientierbare geschlossene Fläche vom Geschlecht g ist b₀ = 1, b₁ = 2g, b₂ = 1.
• Allgemein gilt für jede n-dimensionale orientierbare geschlossene Mannigfaltigkeit die Poincaré-Dualität:

b_k = b_{n − k}.

• Für jede n-dimensionale Mannigfaltigkeit X gilt b_k = 0 für k > n.
• Für zwei topologische Räume X,Y gilt

$b_n(X\times Y)=\sum_{\lambda+\mu=n}b_\lambda(X)b_\mu(Y).$

Beispiele

• Die Bettizahlen der n-Sphäre sind

$b_k(S^n)=\begin{cases}1&\mathrm{f\ddot ur}\ k=0\ \mathrm{und}\ k=n\\0&\mathrm{sonst}\end{cases}.$

• Die Bettizahlen der reellen projektiven Ebene sind 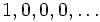$1,0,0,0,\ldots$, genau wie die eines einzelnen Punktes und jeder konvexen Menge im 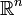$\mathbb R^n$. Zwei sehr verschiedene Räume können also in allen Bettizahlen übereinstimmen.

Verwandte Begriffe

Die Euler-Charakteristik ist die alternierende Summe der Bettizahlen, d.h.

$\chi(X) = b_0(X) - b_1(X) + b_2(X) -+\ldots$

Weblinks

• Eric W. Weisstein: Betti Number auf MathWorld (englisch)