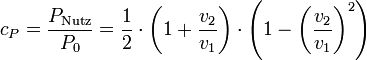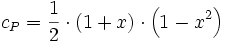- Betz'sches Gesetz
-
Das Betzsche Gesetz stammt von dem deutschen Ingenieur Albert Betz (1885-1968). Er formulierte es erstmals im Jahr 1919. Sieben Jahre später (1926) erschien es in seinem Buch „Wind-Energie“.
Das Gesetz besagt, dass eine Windkraftanlage maximal 16/27 (das sind knapp 60 Prozent) der im Wind enthaltenen translatorischen Energie in rotatorische Energie umwandeln kann (dies gilt nur für Auftriebsläufer.). Dieser Wert ist kein Wirkungsgrad im eigentlichen Sinne, sondern ein Erntegrad, da die ungenutzte Energie in der Strömung, die am Rotor vorbeistreicht, sowie in der abgebremsten Strömung erhalten bleibt und nicht umgewandelt wird.
Der britische Ingenieur Frederick W. Lanchester (1868-1946) publizierte schon 1915 ähnliche Überlegungen.
Inhaltsverzeichnis
Mathematische Herleitung
Leistungsbeiwert
Der Quotient aus genutzter Windleistung PNutz zu ankommender Windleistung P0 wird Leistungsbeiwert cP genannt.
Die Leistung des ankommenden Windes beträgt
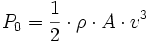 ,
,
genutzt werden kann aber nur
![\ P_{\text{Nutz}} = {1 \over 2}\cdot \rho \cdot A \cdot v^3\cdot \left[ {1 \over 2}\cdot \left( 1+ \frac{v_2}{v_1} \right)\cdot \left( 1- \left(\frac{v_2}{v_1}\right)^2 \right) \right]](/pictures/dewiki/50/216396a6961e0d0cf1d54e39f990f706.png) ,
,
wobei v=v1 die Windgeschwindigkeit weit vor dem Rotor und v2 die Windgeschwindigkeit weit hinter dem Rotor ist. Daraus ergibt sich als Verhältnis der Leistungsbeiwert cP zu:
Führt man die dimensionslose Abbremsung
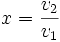 ein, so erhält man als Leistungsbeiwert:
ein, so erhält man als Leistungsbeiwert:Der Leistungsbeiwert ist also ausschließlich eine Funktion der Abbremsung. Wie diese Abbremsung vorgenommen wird, geht in die Berechnung nicht ein. In der Praxis lassen sich hohe Leistungsbeiwerte jedoch ausschließlich mit Auftriebsläufern erreichen.
Betzscher Leistungsbeiwert
Wenn der Windströmung (kinetische) Energie entnommen wird, verlangsamt sich der Wind. Würde die Energie vollständig entnommen, dann kämen die Luftmassen hinter der Anlage zum Stillstand und würden sich vor ihr aufstauen und ausweichen, sodass der Massenstrom durch die Anlage und die Leistung Null wäre. (Aus diesem Grund verliert das Betzsche Gesetz für kleine Geschwindigkeitsverhältnisse v2/v1 seine Gültigkeit, denn bei Ableitung des Gesetzes wird davon ausgegangen, dass die Windgeschwindigkeit in der Rotorebene (v1+v2)/2 ist.) Würde der Wind dagegen gar nicht abgebremst, so nähme der Massenstrom zwar nicht ab, aber es würde auch keine Energie entnommen, und die Leistung wäre wiederum Null. Der Idealfall liegt also irgendwo dazwischen.
Die Herleitung erfolgt mithilfe der Differentialrechnung; wo die Funktion ihr Maximum hat, muss die Ableitung der Funktion eine Nullstelle haben.
Die Ableitung hat bei
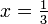 eine Nullstelle;
eine Nullstelle;eingesetzt ergibt sich
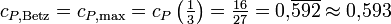 .
.Die größte Leistung lässt sich also entziehen (anders ausgedrückt: der größte Erntegrad erreichen), wenn der Wind auf ein Drittel seiner ursprünglichen Geschwindigkeit abgebremst wird.
Möglichkeiten zur Überwindung
Es wird des Öfteren behauptet, ein cP > cP,Betz erhalten zu haben. Wegen der Allgemeinheit der Herleitung ist dies jedoch praktisch fast so unmöglich wie eine Verletzung des Erhaltungssatzes der Energie. Man muss beachten, dass die Wahl der Bezugsfläche entscheidend ist: Sie ist als größte Projektion der vom Rotor überstrichenen Fläche in Windrichtung zu wählen. Wird einer gemantelten Windturbine ein „Über-Betzwert“ zugesprochen, so liegt auch dies vermutlich an der falschen Wahl der Bezugsfläche: Statt der Rotorfläche muss nun die größte Stirnfläche der Anlage benutzt werden, also in den meisten Fällen die Austrittsfläche des Mantels oder Diffusors.
Bisher ist nur ein theoretisch möglicher Ausweg bekannt, der bereits von Betz selbst angegeben wurde: Wird dem als einzelne, unendlich dünne „Wirkscheibe“ (engl. actuator disk) modellierten Rotor eine endliche Dicke zugesprochen, so könnten quer zur Hauptströmung vorhandene turbulente Fluktuationen zusätzliche Energie in das Volumen zwischen den beiden stromauf und stromab zu unterscheidenden Wirkscheiben einbringen.
Diese Idee wurde von Loth und McCoy 1983 detailliert für einen Darrieus-Rotor mit vertikaler Rotationsachse ausgearbeitet. Sie erhielten cP ≈ 0,62. Allerdings wurde dieser Wert noch in keiner Anlage gemessen.
Ein konifizierter Rotor mit horizontaler Drehachse scheint ebenfalls keine messbare Leistungssteigerung zu erbringen.
Ausgeführte Rotoren
Da die Rotorverluste die mit Abstand größten Verluste einer Windkraftanlage sind, arbeiten alle Hersteller daran, möglichst hohe Leistungsbeiwerte zu erreichen. Moderne ausgeführte Rotoren erreichen Leistungsbeiwerte von cP = 0,4 bis 0,5, das sind also etwa 70 % bis 80 % des theoretisch Möglichen.
Literatur
- Albert Betz: Windenergie und ihre Ausnutzung durch Windmühlen, Ökobuch, Staufen, unveränderter Nachdruck aus dem Jahre 1926, ISBN 3-922964-11-7
- Robert Mikkelsen: Actuator Disc Methods Applied to Wind Turbines, Dissertation, Technical University of Denmark, 2003
- John L. Loth und Hugh McCoy: Optimization of Darrieus Turbines with an Upwind and Downwind Momentum Model, Journal of Energy, Band 4, pp 313-318, 1983
- Derek Grant Phillips: An Investigation on Diffuser Augmented Wind Turbine Design, Dissertation, The University of Auckland, 2003
Weblinks
Wikimedia Foundation.