- Beweisbar
-
Unter einer Ableitung oder Herleitung versteht man in der Logik
- die Gewinnung von Sätzen aus anderen Sätzen in einem formalen Kalkül nach den im Kalkül zugelassenen Regeln (herrschender syntaktisch-formaler Ableitungsbegriff)[1] oder
- den Nachweis der Allgemeingültigkeit eines Schlusses von bestimmten Prämissen (Hypothesen) auf die Konklusion (These)[2]
Inhaltsverzeichnis
Ableitung im formalen Sinn
In der mathematischen Logik bedeutet Ableitung eine formale Folgerung von (neuen) Aussagen aus einer Menge von gegebenen Aussagen. Die zulässigen Schlussregeln sind in einem Kalkül definiert.
Die einfache Anwendung einer solchen Regel auf Aussagen nennt man einen Ableitungsschritt.
Eine Aussage φ heißt ableitbar oder beweisbar aus einer gegebenen Menge Θ von Aussagen, wenn sie durch eine endliche Folge von Ableitungsschritten erreicht werden kann, wobei man von einer (ggf. leeren) Aussagenmenge Θ, den Prämissen oder Annahmen, ausgeht.
Fügt man alle ableitbaren Aussagen zur Aussagenmenge hinzu (man sagt, man bildet den deduktiven Abschluss), so erhält man eine Theorie.
Beispiel (vgl. Aussagenlogik):
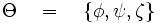
sei als Aussagenmenge gegeben und eine Ableitungsregel des Kalküls sei
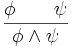 ,
,so kann z. B.
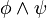 und
und 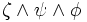 abgeleitet werden.
abgeleitet werden.Bei der Ableitbarkeitsrelation (bzw. dem Ableitbarkeitsbegriff, auch Inferenzrelation) handelt es sich um eine Relation zwischen einer Menge von Aussagen, den Prämissen, und einer einzelnen Aussage, der Konklusion. Für die Ableitbarkeit wird oft das Symbol
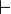 verwendet.
verwendet. 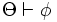 ist dabei zu lesen als: "aus Θ ist φ ableitbar". Führen wir obiges Beispiel fort, so können wir schreiben:
ist dabei zu lesen als: "aus Θ ist φ ableitbar". Führen wir obiges Beispiel fort, so können wir schreiben: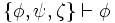 ,
, 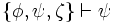 ,
, 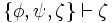 ,
, 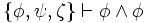 ,
, 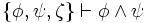 ,
, 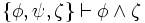 ,
, 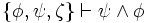 ,
, 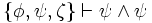 usw.
usw.Unterschiedliche Logiken definieren jeweils einen unterschiedlichen Ableitbarkeitsbegriff. So gibt es einen aussagenlogischen Ableitbarkeitsbegriff, einen prädikatenlogischen, einen Intuitionistischen, einen modallogischen usw.
Obwohl es also unterschiedliche Ableitbarkeitsrelationen gibt, gibt es doch eine Reihe von Eigenschaften, die den meisten Ableitbarkeitsrelationen (zumindest den obengenannten) gemeinsam sind
- Inklusion:
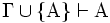 (Jede Annahme ist auch eine Folgerung).
(Jede Annahme ist auch eine Folgerung). - Idempotenz: Wenn
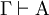 und
und 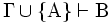 , dann
, dann 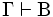 (Durch Hinzunahme von Folgerungen zu den Annahmen erhält man keine neuen Folgerungen.)
(Durch Hinzunahme von Folgerungen zu den Annahmen erhält man keine neuen Folgerungen.) - Monotonie: Wenn
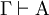 , dann
, dann  (Hinzufügen von Annahmen erhält die bisher möglichen Folgerungen.)
(Hinzufügen von Annahmen erhält die bisher möglichen Folgerungen.) - Kompaktheit; Wenn
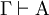 , dann gibt es eine endliche Menge Δ mit
, dann gibt es eine endliche Menge Δ mit 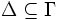 , so dass
, so dass 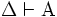 . (Jede Folgerung aus einer unendlichen Annahmenmenge ist bereits aus einer endlichen Teilmenge zu erreichen.)
. (Jede Folgerung aus einer unendlichen Annahmenmenge ist bereits aus einer endlichen Teilmenge zu erreichen.)
Siehe auch: Inferenzoperation; KalkülAbleitung im materiellen Sinn
Da es bei der Ableitung im formalen Sinn [1] lediglich um "die Erzeugung eines Zeichengebildes aus einem anderen nach den Regeln des jeweiligen Kalküls"[3] geht und ein Kalkül "nichts anderes als eine Herstellungsvorschrift für Figuren (ist)[4] ist "das Ableiten ..kein logisches Schließen, denn die Vorschriften des Kalküls, also die Grundfiguren und die Grundregeln, können ja ganz willkürlich gewählt sein“[5].
Von der Ableitung im formalen Sinn eines Kalküls ist der Nachweis der Allgemeingültigkeit des Schlusses von bestimmten Voraussetzungen auf eine Konklusion zu unterscheiden[6].
Die Begriffe der formalen und der materiellen Ableitung[7] hängen miteinander zusammen: Eine formale Ableitbarkeit besteht im Allgemeinen, wenn auch eine materielle Ableitbarkeit besteht.
Beispiel[8]:
In Verbindung mit der Abtrennungsregel ist im aussagenlogischen Kalkül folgende Ableitung möglich:
- Die Beatles spielten Kammermusik.
- Wenn die Beatles Kammermusik spielten, verdienten sie viel Geld.
- Die Beatles verdienten viel Geld.
Zugleich liegt ein allgemeingültiger Schluss vor.
Siehe auch
Quellen
- ↑ Schülerduden Philosophie, 2. Aufl. (2002)/Ableitung spricht von "Ableitung i.S.d. formalen Logik"
- ↑ Schülerduden Philosophie, 2. Aufl. (2002)/Ableitung spricht von "Ableitung i.S.d. inhaltlichen Logik"
- ↑ Seiffert, Wissenschaftstheorie IV (1997), Ableitung
- ↑ Lorenzen, Logik, 4. Aufl. (1970), S. 58
- ↑ Lorenzen, Logik, 4. Aufl. (1970), S. 58
- ↑ Regenbogen/Meyer, Wörterbuch der Philosophischen Begriffe (2005)/Ableitung; Schülerduden Philosophie, 2. Aufl. (2002)/Ableitung
- ↑ Der Ausdruck "materielle Ableitbarkeit" wird hier eingeführt. Schülerduden Philosophie, a.a.O. spricht von der Ableitung im Sinne der inhaltlichen Logik
- ↑ Vgl. Regenbogen/Meyer, Wörterbuch der Philosophischen Begriffe (2005)/Ableitung
Wikimedia Foundation.
