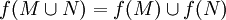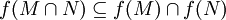- Bildmenge
-
Bei einer mathematischen Funktion f ist das Bild, Bildmenge oder Bildbereich einer Teilmenge M des Definitionsbereichs die Menge der Werte aus der Zielmenge, die f auf M tatsächlich annimmt.[1]
Häufig werden dafür auch die Wörter Wertemenge[2] oder Wertebereich[1] benutzt; andere bezeichnen mit diesen Wörtern aber stattdessen die Zielmenge[3]. Es besteht also Verwechslungsgefahr.
Inhaltsverzeichnis
Definition
Für eine Funktion
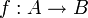 und eine Teilmenge M von A bezeichnet man die folgende Menge als das Bild von M unter f:
und eine Teilmenge M von A bezeichnet man die folgende Menge als das Bild von M unter f:Das Bild von f ist dann das Bild der Definitionsmenge unter f, also:
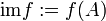 („im“ vom englischen Wort image)
(„im“ vom englischen Wort image)
Alternative Notationen
Für
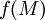 wird auch die Notation
wird auch die Notation ![f[M]\!\,](/pictures/dewiki/99/c1301d3793a989f8033fad55a1a904bf.png) verwendet.
verwendet.Die deutsche Bezeichnung
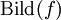 für
für 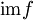 ist ebenfalls gebräuchlich.
ist ebenfalls gebräuchlich.Im allgemeinen nutzt man die übliche Mengennotation, um die Bildmenge darzustellen, in unserem Beispiel: Bildmenge = {A, B, D}.
Beispiele
Für die Funktion
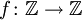 (ganze Zahlen) mit
(ganze Zahlen) mit 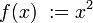 gilt:
gilt:- Wie man sieht führen hier verschiedene Eingabegrößen jeweils auf dieselbe Bildmenge.
- Insgesamt kann man die Menge der Quadratzahlen wie folgt abkürzen:
Eigenschaften
Es sei
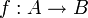 eine Funktion und M und N seien Teilmengen von A:
eine Funktion und M und N seien Teilmengen von A:Die Aussagen über Vereinigung und Durchschnitt lassen sich von zwei Teilmengen auf beliebige Familien von Teilmengen verallgemeinern.
Siehe auch
Einzelnachweise
- ↑ a b Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6. S 106
- ↑ Reinhard Dobbener: Analysis. Oldenbourg Wissenschaftsverlag 2007, ISBN 3486579991. S 12, Definition 1.12
- ↑ Michael Ruzicka: Analysis I. Vorlesung vom Wintersemester 2004/2005. S 21
Wikimedia Foundation.


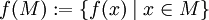
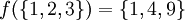
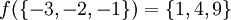
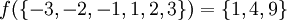
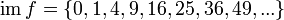
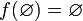
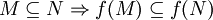
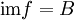 .
.