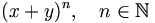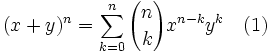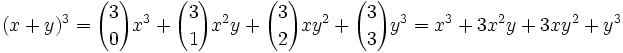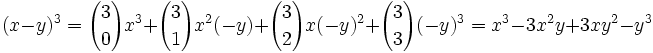- Binomialentwicklung
-
Der binomische Lehrsatz ist ein Satz der Mathematik, der es in seiner einfachsten Form ermöglicht, die Potenzen eines Binoms x+y, also einen Ausdruck der Form
als Polynom n-ten Grades in den Variablen x und y auszudrücken.
Dieser Satz zählt in seiner allgemeinen Form mit einem reellen oder gar komplexen Exponenten zu den erstaunlichsten mathematischen Theoremen. Auf einer 1999 veröffentlichten Liste der 100 erstaunlichsten mathematischen Sätze[1] ist er auf Platz 44 gelistet.
In der Algebra gibt der binomische Lehrsatz an, wie ein Ausdruck der Form (x + y)n auszumultiplizieren ist.
Inhaltsverzeichnis
Binomischer Lehrsatz für natürliche Exponenten
Für alle Elemente x und y eines kommutativen unitären Rings und für alle natürlichen Zahlen
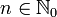 gilt die Gleichung:
gilt die Gleichung:Insbesondere gilt dies für reelle oder komplexe Zahlen x und y. (Man beachte dabei 00 = 1.)
Die Koeffizienten dieses Polynomausdrucks sind die Binomialkoeffizienten
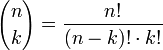 ,
,
die ihren Namen aufgrund ihres Auftretens im binomischen Lehrsatz erhalten haben. Mit
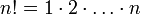 ist hierbei die Fakultät von n bezeichnet.
ist hierbei die Fakultät von n bezeichnet.Bemerkung
Die Terme
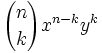 sind dabei als Skalarmultiplikation der ganzen Zahl
sind dabei als Skalarmultiplikation der ganzen Zahl 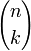 an das Ringelement xn − kyk aufzufassen, d. h. hier wird der Ring in seiner Eigenschaft als
an das Ringelement xn − kyk aufzufassen, d. h. hier wird der Ring in seiner Eigenschaft als 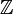 -Modul benutzt.
-Modul benutzt.Spezialisierung
Der binomische Lehrsatz für den Fall n = 2 heißt erste Binomische Formel.
Verallgemeinerungen
- Der binomische Lehrsatz gilt auch in beliebigen unitären Ringen, sofern nur x und y miteinander kommutieren, d.h.
 gilt.
gilt. - Auch die Existenz der Eins im Ring ist verzichtbar, sofern man den Lehrsatz in folgende Form umschreibt:
![(x+y)^n = x^n + \left[ \sum_{k=1}^{n-1}{n \choose k} x^{n-k}y^{k} \right] + y^n](/pictures/dewiki/97/aaea4dc5e8cbf6e6ec7190f8b620493e.png) .
.
- Für mehr als zwei Summanden gibt es den polynomischen Lehrsatz.
Herleitung
Der Beweis [1] funktioniert durch Induktion über n; für jedes konkrete n kann man diese Formel auch durch Ausmultiplizieren erhalten.
Beispiel
Binomische Reihe, Lehrsatz für komplexe Exponenten
Eine Verallgemeinerung des Theorems auf beliebige reelle Exponenten α mittels unendlicher Reihen ist Isaac Newton zu verdanken. Dieselbe Aussage ist aber auch gültig, wenn α eine beliebige komplexe Zahl ist.
Der binomische Lehrsatz lautet in seiner allgemeinen Form:
 .
.
Diese Reihe konvergiert für alle
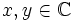 mit | x / y | < 1.
mit | x / y | < 1.Im Spezialfall
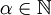 geht Gleichung (2) in (1) über und ist dann sogar für alle
geht Gleichung (2) in (1) über und ist dann sogar für alle 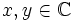 gültig, da die Reihe dann abbricht.
gültig, da die Reihe dann abbricht.Die hier gebrauchten verallgemeinerten Binomialkoeffizienten sind definiert als
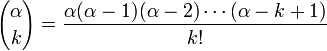 .
.
Im Fall k = 0 entsteht ein leeres Produkt, dessen Wert als 1 definiert ist.
Für α = -1 und y = 1 ergibt sich aus (2) als Sonderfall die geometrische Reihe.
Literatur
- M. Barner, F. Flohr: Analysis I, de Gruyter, 2000, ISBN 3-11-016778-6.
Einzelnachweise
Wikimedia Foundation.