- Birefringenz
-
Als Doppelbrechung (engl. birefringence) wird in der Optik die Eigenschaft von nichtkubischen (optisch anisotropen) Materialien bezeichnet, ein Lichtbündel in zwei senkrecht zueinander polarisierte Teilbündel aufzuspalten (vgl. Brechung). Die Ursache dieses Effekts liegt in unterschiedlichen Brechzahlen (no und nao) in Abhängigkeit von der Ausbreitungsrichtung und Polarisation des Lichtes. Ein prominentes Beispiel für ein solches Material ist Calcit (Kalkspat, auch Doppelspat), an dem die Doppelbrechung 1669 von Erasmus Bartholin entdeckt wurde.
 Doppelbrechung beim Calcit
Doppelbrechung beim Calcit Aufspaltung eines Laser-Strahles in Calcit
Aufspaltung eines Laser-Strahles in CalcitAuch isotrope Materialien können durch äußere Einflüsse, wie mechanische Spannung (Deformations- oder Spannungsdoppelbrechung), elektrische Felder (elektrische Doppelbrechung, Kerr-Effekt) oder magnetische Felder (magnetische Doppelbrechung, Cotton-Mouton-Effekt), doppelbrechend werden. Auch Flüssigkeiten mit hoher Zähigkeit können bei Strömung durch innere Reibung doppelbrechend wirken.
Eng verwandt mit der Doppelbrechung ist der Dichroismus.
Inhaltsverzeichnis
Physikalische Ursache für den Effekt
Doppelbrechung tritt in solchen Kristallen auf, die optisch anisotrop sind. Dies bedeutet, dass sie verschiedene Brechzahlen für verschiedene Polarisationen und Richtungen des eingestrahlten Lichtes aufweisen. Dies lässt sich mit dem Brechzahl-Ellipsoid (auch Indikatrix genannt) darstellen. Dieses Ellipsoid kann ein Rotationsellipsoid, d. h. „optisch einachsig“, sein (z. B. bei tetragonalen Kristallen) oder drei verschiedene Hauptachsen besitzen (z. B. bei orthorhombischer Symmetrie). In diesem besonderen Fall, d. h. bei „optisch zweiachsigen“ Kristallen (biaxial), sind im Allgemeinen beide gebrochenen Strahlen „außerordentlich“ (elektrisches Feld,
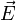 , und dielektrische Induktion,
, und dielektrische Induktion, 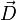 , haben nicht die gleiche Richtung, wobei der Ausbreitungsvektor,
, haben nicht die gleiche Richtung, wobei der Ausbreitungsvektor, 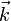 , senkrecht zu
, senkrecht zu 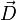 ist, nicht wie sonst üblich, zu
ist, nicht wie sonst üblich, zu 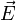 , siehe Literatur).
, siehe Literatur).In optisch einachsigen Kristallen breitet sich der ordentliche Strahl, dessen elektrisches Feld immer senkrecht zur optischen Achse des Kristalls steht, wie in einem nicht doppelbrechenden Material aus, ist also transversal zur Ausbreitungsrichtung. Dagegen hat das elektrische Feld des außerordentlichen Strahls, der senkrecht zum ordentlichen polarisiert ist, eine Komponente parallel zur Ausbreitungsrichtung. Beide Komponenten bzgl. der optischen Achse haben unterschiedliche Ausbreitungsgeschwindigkeiten,
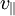 bzw.
bzw. 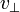 , was dazu führt, dass der außerordentliche Strahl im Material bzgl. der Richtung des ordentlichen Strahls etwas geneigt ist.
, was dazu führt, dass der außerordentliche Strahl im Material bzgl. der Richtung des ordentlichen Strahls etwas geneigt ist.Man kann zu den genannten Geschwindigkeiten Brechzahlen definieren:
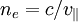 ,
, 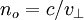 , wobei c die Vakuum-Lichtgeschwindigkeit ist. Die Differenz der Brechzahlen Δn = ne − n0 ist ein Maß für die Doppelbrechung, das Vorzeichen wird als optischer Charakter (oder optische Orientierung) bezeichnet. Für Kalkspat ist Δn = − 0,172, man nennt ihn auch optisch negativ.
, wobei c die Vakuum-Lichtgeschwindigkeit ist. Die Differenz der Brechzahlen Δn = ne − n0 ist ein Maß für die Doppelbrechung, das Vorzeichen wird als optischer Charakter (oder optische Orientierung) bezeichnet. Für Kalkspat ist Δn = − 0,172, man nennt ihn auch optisch negativ.Da es in optisch aktiven Substanzen unterschiedliche Brechzahlen für links- und rechts-zirkular polarisiertes Licht gibt, spricht man in diesem Fall auch von zirkularer Doppelbrechung.
Tabellen
Die beiden folgenden Tabellen auf der rechten Seite enthalten Daten gängiger uniaxialer bzw. biaxialer Systeme. 'D' ist die oben angegebene Differenz der Brechzahlen für den außerordentlichen (
 ) bzw. für den ordentlichen Strahl:
) bzw. für den ordentlichen Strahl:Uniaxiale Kristalle, für λ=590 nm[1] Material no ne D Beryll Be3Al2(SiO3)6 1,602 1,557 −0,045 Kalkspat CaCO3 1,658 1,486 −0,172 Kalomel Hg2Cl2 1,973 2,656 +0,683 Eis H2O 1,309 1,313 +0,014 Lithiumniobat LiNbO3 2,272 2,187 −0,085 Magnesiumfluorid MgF2 1,380 1,385 +0,006 Quarz SiO2 1,544 1,553 +0,009 Rubin Al2O3 1,770 1,762 −0,008 Rutil TiO2 2,616 2,903 +0,287 Peridotit (Mg, Fe)2SiO4 1,690 1,654 −0,036 Saphir Al2O3 1,768 1,760 −0,008 Natriumnitrat NaNO3 1,587 1,336 −0,251 Turmalin (komplexes Silikat) 1,669 1,638 −0,031 a-Zirkon ZrSiO4 1,960 2,015 +0,055 b-Zirkon ZrSiO4 1,920 1,967 +0,047 Biaxiale Kristalle, für λ= 590 nm[1] Material na nß n? Borax 1,447 1,469 1,472 Epsomsalz MgSO4·7(H2O) 1,433 1,455 1,461 Glimmer, Biotit 1,595 1,640 1,640 Glimmer, Muskovit 1,563 1,596 1,601 Olivin (Mg, Fe)2SiO4 1,640 1,660 1,680 Perovskit CaTiO3 2,300 2,340 2,380 Topas 1,618 1,620 1,627 Ulexit 1,490 1,510 1,520 Anwendung von doppelbrechenden Materialien
Doppelbrechende Materialien werden z. B. in Wellenplatten und Polarisatoren verwendet. Man kann aus unpolarisiertem Licht so linear polarisisertes Licht erzeugen. Zu den doppelbrechenden Polarisatoren zählen unter anderem das Nicolsche Prisma, das Glan-Thompson-Prisma oder das λ/4-Plättchen.
Doppelbrechung kann auch beim Spritzpressen von CDs auftreten.[2] Verursacht wird die Doppelbrechung durch mechanische Verspannungen innerhalb der Polycarbonat-Schicht, beispielsweise durch thermischen Belastung oder Scherbeanspruchung des Materials.
Nachweis doppelbrechender Materialien
Der Nachweis einer doppelbrechenden Substanz erfolgt z.B. über die Polarisationsmikroskopie. Bei Drehung der Probe zwischen gekreuzten Polarisationsfiltern ändert sich die Helligkeit bzw. die Farbe des doppelbrechenden Objektes, während optisch isotrope Materialien keine Veränderungen im Bild zeigen.
Literatur
- Werner Döring: Einführung in die Theoretische Physik, Band III (Optik). Sammlung Göschen, Berlin 1957.
Siehe auch
Weblinks
Einzelnachweise
- ↑ a b Elert, Glenn. Refraction. The Physics Hypertextbook.
- ↑ R. Wimberger-Friedl: Analysis of the birefringence distributions in compact discs of polycarbonate. In: Polymer Engineering & Science. 30, Nr. 14, 1990, S. 813–820 (doi:10.1002/pen.760301403).
Wikimedia Foundation.



