- Blasensortierung
-
Das Sortieren durch Aufsteigen (englisch Bubble sort, "Blasensortierung") bezeichnet einen einfachen, stabilen Sortieralgorithmus, der eine Reihe zufällig angeordneter Elemente (etwa Zahlen) der Größe nach ordnet.
Bubblesort wird von Donald E. Knuth als vergleichsbasierter Sortieralgorithmus bezeichnet [1]. Das bedeutet, dass der Sortieralgorithmus sämtliche Entscheidungen alleine auf Basis des Größenvergleichs je zweier Elemente fällt, nicht etwa aufgrund der Inspektion der Binärdarstellung eines Elements. Bubblesort ist der einfachste solcher Algorithmen. Einzige Anforderung an den Vergleichsoperator ist, dass er eine Totalordnung der Liste ermöglicht.
Bubblesort gehört zur Klasse der In-place-Verfahren, was bedeutet, dass der Algorithmus zum Sortieren keinen zusätzlichen Arbeitsspeicher außer den lokalen Laufvariablen der Prozedur benötigt. Dadurch, dass grundsätzlich nur aneinandergrenzende Elemente miteinander vertauscht werden, eignet sich dieses Verfahren auch zum Sortieren von Listen mit unterschiedlich großen Elementen.
Wegen der einerseits mangelhaften Effizienz und anderseits breiten Verfügbarkeit deutlich besserer Alternativen wird Bubblesort meistens nur als Beispiel für einen schlechten oder naiven Sortieralgorithmus verwendet.
Inhaltsverzeichnis
Prinzip
Der Algorithmus vergleicht der Reihe nach zwei benachbarte Elemente und vertauscht sie, falls sie in der falschen Reihenfolge vorliegen. Dieser Vorgang wird solange wiederholt, bis keine Vertauschungen mehr nötig sind. Hierzu sind in der Regel mehrere Durchläufe erforderlich.
Je nachdem, ob auf- oder absteigend sortiert wird, steigen die größeren oder kleineren Elemente wie Blasen im Wasser (daher der Name) immer weiter nach oben, das heißt, an das Ende der Reihe. Auch werden immer zwei Zahlen miteinander in „Bubbles“ vertauscht.
Formaler Algorithmus
Der Algorithmus sieht im Pseudocode so aus:
prozedur bubbleSort( A : Liste sortierbarer Elemente ) n := Länge( A ) wiederhole vertauscht := falsch für jedes i von 1 bis n - 1 wiederhole falls A[ i ] > A[ i + 1 ] dann vertausche( A[ i ], A[ i + 1 ] ) vertauscht := wahr falls ende für ende n := n - 1 solange vertauscht und n >= 1 prozedur endeDie äußerste Schleife durchläuft die zu sortierenden Daten, bis keine Vertauschungen mehr nötig sind. In dieser Schleife wird das Feld jeweils einmal durchlaufen und es werden zwei benachbarte Daten vertauscht, wenn sie in falscher Reihenfolge stehen.
Analyse
Schlimmster Fall
Bubblesort hat die Laufzeit
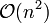 für Listen der Länge n. Im Falle der umgekehrt sortierten Liste (n,n-1,...,2,1) werden maximal
für Listen der Länge n. Im Falle der umgekehrt sortierten Liste (n,n-1,...,2,1) werden maximal 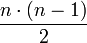 viele Vertauschungen ausgeführt: um das erste (und größte) Element n ganz nach rechts zu bewegen, werden n − 1 Vertauschungen vorgenommen. Allgemein: Die Bewegung des k-ten Elements an die Stelle n − k wird durch n − k Vertauschungen vollzogen. Aufsummieren über alle k ergibt im Ganzen
viele Vertauschungen ausgeführt: um das erste (und größte) Element n ganz nach rechts zu bewegen, werden n − 1 Vertauschungen vorgenommen. Allgemein: Die Bewegung des k-ten Elements an die Stelle n − k wird durch n − k Vertauschungen vollzogen. Aufsummieren über alle k ergibt im Ganzen 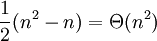 Vertauschungen. Da nur Paare vertauscht werden, die auch vorher verglichen wurden, benötigt der Algorithmus auch mindestens ebenso viele Vergleiche. Betrachtet man den Pseudocode des Algorithmus, so sieht man leicht ein, dass keine der Anweisungen öfter als
Vertauschungen. Da nur Paare vertauscht werden, die auch vorher verglichen wurden, benötigt der Algorithmus auch mindestens ebenso viele Vergleiche. Betrachtet man den Pseudocode des Algorithmus, so sieht man leicht ein, dass keine der Anweisungen öfter als 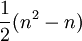 mal ausgeführt werden kann, also ist dies auch die bestmögliche untere Schranke.
mal ausgeführt werden kann, also ist dies auch die bestmögliche untere Schranke.Bester Fall
Falls die Liste bereits sortiert ist, wird Bubblesort die Liste nur einmal durchgehen, um festzustellen, dass die Liste bereits sortiert ist, weil keine benachbarten Elemente vertauscht werden mussten. Daher benötigt Bubblesort
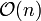 Schritte, um eine bereits sortierte Liste zu bearbeiten.
Schritte, um eine bereits sortierte Liste zu bearbeiten.Falls die Elemente der Liste bereits nah den Stellen sind, die sie nach der Sortierung bekommen sollen, ist die Laufzeit erheblich besser als
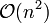 .
.Durchschnittlicher Fall
Die erwartete Anzahl der Vergleiche für eine zufällig gewählte Permutation der Liste (1,2,...,n) ist
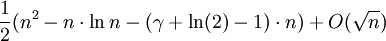 ,
,wobei γ die Euler-Mascheroni-Konstante bezeichnet; die erwartete Anzahl der Vertauschungen beträgt
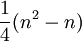 , siehe [2], S. 108ff.
, siehe [2], S. 108ff.Hasen und Schildkröten
Die Positionen der Elemente vor dem Sortieren entscheiden maßgeblich den Sortieraufwand. Große Elemente am Anfang wirken sich nicht gravierend aus, da sie schnell nach hinten getauscht werden, kleine Elemente am Ende bewegen sich jedoch eher langsam nach vorne. Darum spricht man bei diesen Elementen von Hasen und Schildkröten.
Verschiedene Anstrengungen wurden unternommen, um die Geschwindigkeit der Schildkröten zu verbessern. Ein Algorithmus, der sie erheblich verbessert, ist Cocktailsort, der allerdings im schlimmsten Fall immer noch
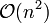 Schritte benötigt. Combsort vergleicht Elemente, die weit von einander entfernt sind, und kann Schildkröten darum schnell bewegen, bevor die kleineren Sortierungen vorgenommen werden. Dessen Komplexität ist mit schnelleren Algorithmen wie Quicksort vergleichbar.
Schritte benötigt. Combsort vergleicht Elemente, die weit von einander entfernt sind, und kann Schildkröten darum schnell bewegen, bevor die kleineren Sortierungen vorgenommen werden. Dessen Komplexität ist mit schnelleren Algorithmen wie Quicksort vergleichbar.Beispiel
Eine Reihe von fünf Zahlen soll aufsteigend sortiert werden.
Die fett gedruckten Zahlen werden jeweils verglichen. Ist die linke größer als die rechte, so werden beide vertauscht; das Zahlenpaar ist dann blau markiert. Im ersten Durchlauf wandert somit die größte Zahl ganz nach rechts. Der zweite Durchlauf braucht somit die letzte und vorletzte Position nicht mehr zu vergleichen. --> Dritter Durchlauf: kein Vergleich letzte/vorletzte/vorvorletzte....
55 07 78 12 42 1. Durchlauf
07 55 78 12 42
07 55 78 12 42
07 55 12 78 42 Letzter Vergleich
07 55 12 42 78 2. Durchlauf
07 55 12 42 78
07 12 55 42 78 Letzter Vergleich
07 12 42 55 78
07 12 42 55 78 3. Durchlauf
07 12 42 55 78 Letzter Vergleich
07 12 42 55 78
07 12 42 55 78
07 12 42 55 78 Fertig sortiert.Siehe auch
Weblinks
- [1] - Bubblesort als Flussdiagramm dargestellt (Chr. Everke, 05/2008 ITA)
- VisuSort Framework - Visualisierung diverser Sortieralgorithmen (Windows)
- Visualisierung von BubbleSort
- http://olli.informatik.uni-oldenburg.de/fpsort/Animation.html - interaktive Animation des Verfahrens mit Codebeispielen
- http://www.inf.ethz.ch/~staerk/algorithms/SortAnimation.html - Java-Beispiele für Sortieralgorithmen
- Bubblesort Source Code
- Bubblesort c,c++,c#,php Code
Einzelnachweise
- ↑ D. E. Knuth. The Art of Computer Programming. Volume 3: Sorting and Searching, Second Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 5.3.1: Minimum-Comparison Sorting, pp.180–197
- ↑ Knuth, Donald E.: The Art of Computer Programming, Vol. 3: Sorting and Searching (englisch), 2nd Edition, Addison-Wesley, 1981
Wikimedia Foundation.

