- Blattsuchbaum
-
Der B+-Baum ist eine Erweiterung des B-Baumes. Bei einem B+-Baum werden die eigentlichen Datenelemente nur in den Blattknoten gespeichert, während die inneren Knoten lediglich Schlüssel enthalten.
Ziel dieses Verfahrens ist es, die Zugriffszeiten auf die Datenelemente zu verbessern. Dazu muss man die Baumhöhe verringern, was bedeutet, dass der Verzweigungsgrad des Baumes wachsen muss. Da die maximale Speicherbelegung eines Knotens begrenzt ist, gewinnt man durch das Verlegen der Daten in die Blätter mehr Platz für Schlüssel bzw. Verzweigungen in den inneren Knoten.
Ein weiteres Ziel kann sein, die Operation Bereichssuche zu verbessern, bei der alle Daten in einem gewissen Schlüsselintervall sequentiell durchlaufen werden. Werden die Daten nämlich ausschließlich in den Blättern abgelegt, muss der jeweils nächste Datensatz der Sequenz nicht wieder von der Wurzel aus gesucht werden.
Sei s der Schlüssel des aktuellen Datensatzes der Sequenz. Ist dieser Schlüssel nicht an rechtester Stelle in einem Blatt abgelegt, so befindet sich sein nachfolgender Datensatz (mit dem Schlüssel s') im selben Blatt rechts neben s. Ist der Schlüssel doch an rechtester Stelle eines Blattes gespeichert, müsste die Suche wiederum bei der Wurzel beginnen. Dies kann vermieden werden, indem man die Blätter des B+-Baumes, wie beim B*-Baum, in einer linearen Liste miteinander verbindet. Dieses Feature wird häufig in die Definition des B+-Baumes mit aufgenommen.
Wesentlicher Vorteil eines externen Suchbaums (Daten nur in den Blättern), ist die Möglichkeit des Einsatzes von Sekundärindizes. Sie stellen einen weiteren – nach anderen Kriterien sortierbaren – Suchbaum auf denselben Daten zur Verfügung.
Inhaltsverzeichnis
Struktur
Jeder Knoten besteht aus n Suchschlüsseln und n + 1 Pointern. Davon zeigt in den Blattknoten der letzte Pointer immer auf das nächstliegende Blatt (außer dem letzten Knoten). Die restlichen Pointer in den Blattknoten zeigen jeweils auf die Datenelemente, die durch die Suchschlüssel repräsentiert werden.
Beispiel: n = 3
- alle Knoten haben maximal 3 Suchschlüsselwerte und maximal 4 Pointer
- Wurzel hat mindestens einen Wert, also 2 Pointer
- Innere Knoten haben mindestens 1 Suchschlüssel und 2 Pointer
- Blätter haben mindestens 2 Suchschlüssel und 3 Pointer
Regeln
- Wurzel: Mindestens zwei Pointer besetzt
- Mittelknoten: Mindestfüllgrad
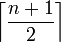 Pointer
Pointer - Blätter: Mindestfüllgrad
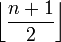 Pointer (zeigen auf Datenblöcke, Pointer auf Nachbarknoten werden nicht gezählt)
Pointer (zeigen auf Datenblöcke, Pointer auf Nachbarknoten werden nicht gezählt)
Für Mittel- und Wurzelknoten gilt: Der links unter einem Suchschlüssel startende Pointer führt zu einem Knoten, dessen größter Suchschlüsselwert kleiner dem Suchschlüsselwert ist. Der rechts unter einem Suchschlüssel stehende Pointer führt zu einem Knoten, dessen kleinster Suchschlüsselwert größer gleich dem Suchschlüsselwert ist.
Suchen
Beispiel anhand von obiger Grafik:
- Suche von Wert „9“: Start im Wurzelknoten, Wert ist größer als 5, also gehe rechten Weg den Pointer entlang, durchsuche Blatt, nicht gefunden, Suche erfolglos.
- Suche von Wert „2“: Start im Wurzelknoten, Wert ist kleiner als 3, also gehe linken Weg dem Pointer entlang und durchsuche Blatt, gefunden, Suche erfolgreich.
Einfügen
Es gibt grundsätzlich 2 Möglichkeiten beim Einfügen von neuen Suchschlüsseln: 1. Es gibt im betreffenden Blatt Platz. 2. Es gibt keinen Platz.
Im ersten Fall kann der Wert einfach in das Blatt eingetragen werden. (siehe Suchen)
Im zweiten Fall wird der Wert an das Blatt "virtuell" angefügt. Jetzt ergibt sich eine Überfüllung des Blattes. Es muss also geteilt werden. Dabei ist zu beachten, dass bei ungerader Suchschlüsselanzahl in einem Blatt das linke Teilblatt einen Suchschlüsselwert mehr als das rechte bekommt (Beispiel: n=4, 1 einfügen, links: 3 Werte & rechts 2 Werte). Dies kann möglicherweise eine Kettenreaktion verursachen, die nach oben im Baum durchpropagiert werden muss, da ja die Mittel- und Wurzelknoten angepasst werden müssen.
Löschen
Der Wert wird im Baum gesucht. Wenn er gefunden wird, dann wird der Wert entfernt. Eventuelle Änderungen müssen durch den Baum propagiert werden. Dabei gibt es zu beachten, dass unterbefüllte Knoten mit anderen verschmolzen werden müssen. Hier gibt es durchaus unterschiedliche Techniken. Am gebräuchlichsten sollte es sein, den Knoten mit seinem linken Nachbarn zu verschmelzen (wenn es keinen linken gibt, dann den rechten) und bei Bedarf diesen bei Überfüllung wieder nach obiger Regel zu teilen.
Vorteile
- ist immer balanciert
- für Bereichsanfragen (in Datenbanksystem) optimal geeignet, da immer alle Blätter sortiert und durch Pointer untereinander verbunden, sodass leicht iterierbar
Siehe auch
- 2-3-4-Baum und B*-Baum sind weitere B-Baum-Varianten.
Weblinks
Wikimedia Foundation.

