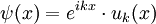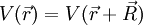- Bloch-Funktionen
-
Die Bloch-Funktion oder Bloch-Welle (nach Felix Bloch) ist die allgemeinste Lösung der stationären Schrödingergleichung für ein x0-periodisches Potential (z. B. die Wellenfunktion eines Elektrons in einem kristallinen Festkörper). Die Form dieser Wellenfunktionen wird durch das Bloch-Theorem festgelegt:
-
Definition: Es sei ein periodisches Potential V(x) mit der Periodizität x0 gegeben, V(x + x0) = V(x). Dann haben die Lösungen der stationären Schrödinger-Gleichung notwendigerweise die Form wobei uk(x) eine periodische Funktion mit Periode x0 ist (uk(x) = uk(x + x0)).
Die Periodizität des Potentials V(x)=V(x+x0) überträgt sich also auf uk(x) und damit auf die Aufenthaltswahrscheinlichkeit |ψ|2 des betrachteten Teilchens im Potential. Betrachtet man einen kristallinen Festkörper, so ist die Periodizität x0 durch das Kristallgitter, also einen Gittervektor gegeben.
Kurze Herleitung
Das Potential
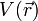 ist invariant gegenüber einer Translation um einen Vektor
ist invariant gegenüber einer Translation um einen Vektor 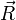 (in einem Kristall ist
(in einem Kristall ist 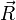 ein Gittervektor):
ein Gittervektor):
Dieselbe Translationsinvarianz gilt damit auch für den Hamiltonoperator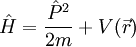 des Teilchens. Daher unterscheiden sich zwei Wellenfunktionen, die um einen Vektor R gegeneinander verschoben sind, höchstens um einen ortsunabhängigen Faktor f:
des Teilchens. Daher unterscheiden sich zwei Wellenfunktionen, die um einen Vektor R gegeneinander verschoben sind, höchstens um einen ortsunabhängigen Faktor f: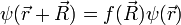 .
.
Bloch zeigte, dass der Faktor f gegeben sein muss durch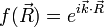 .
.
Diese Bedingungen werden aber gerade durch die Bloch-Funktion erfüllt.Literatur
- Hartmut Haug, Stephan Koch: Quantum Theory of the Optical and Electronic Properties of Semiconductors, Fourth Edition, Singapore – River Edge – London: World Scientific, Seite 29ff.
- Cohen-Tannoudji, Claude / Diu, Bernard / Laloë, Franck (1999): Quantenmechanik 1&2, 2. Auflage, Berlin – New York: Walter de Gruyter.
- Kittel, Charles (2006): Einführung in die Festkörperphysik, 14. Auflage, München: Oldenbourg-Verlag, Seite 194
- Ibach, Harald / Lüth, Hans (1991): Festkörperphysik, 3.Auflage, Berlin – Heidelberg: Springer-Verlag, Seite 106fff
-
Wikimedia Foundation.