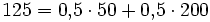Briefumschlagparadox

Das Umtauschparadoxon (oder Briefumschlagparadoxon) beschreibt die paradoxe Situation, dass es bei Kenntnis des Wertverhältnisses zwischen zwei Alternativen und nachdem der Wert einer der Alternativen eröffnet worden ist, stets sinnvoll erscheint, vom angebotenen Umtauschrecht Gebrauch zu machen. Das Paradoxon hinterfragt das naive Rechnen mit Erwartungswerten. Es ist verwandt, aber nicht logisch identisch mit dem Ziegenproblem.

Die Umtauschsituation

Nehmen wir an, Herr Lemke ist ein Gönner von Herrn Schmidt. Die Sekretärin von Herrn Lemke hat zwei gleich aussehende Briefumschläge genommen und in den einen einen Geldbetrag x hinein getan. In den anderen Briefumschlag hat sie den doppelten Betrag hineingetan. Von außen sehen beide Briefumschläge völlig gleich aus. Am Abend treffen sich Herr Lemke und Herr Schmidt auf einer Party. Herr Lemke legt beide Briefumschläge auf einem Tisch ab. Andere Partygäste bringen die Briefumschläge durcheinander. Zur fortgeschrittenen Stunde – man hat schon etwas getrunken – zeigt Herr Lemke die beiden Briefumschläge Herrn Schmidt mit den Worten: „In beiden Briefumschlägen befindet sich ein Geldbetrag, in dem einen doppelt so viel wie im anderen. Ich weiß aber nicht, in welchem wie viel ist. Sie dürfen einen Umschlag öffnen und dann entscheiden, ob Sie die beiden Umschläge austauschen und den anderen nehmen möchten.“ Herr Schmidt ergreift zufällig einen der beiden Umschläge, findet zum Beispiel 100 Euro und überlegt: „Ich habe in diesem Umschlag 100 Euro. Wenn ich tausche, habe ich mit einer Wahrscheinlichkeit von 50% 200 Euro und mit derselben Wahrscheinlichkeit 50 Euro. Dies macht einen Erwartungswert von 125 Euro.“

$125 = 0{,}5 \cdot 50 + 0{,}5 \cdot 200$

Lohnt sich das Tauschen?

Das Paradoxon

Wenn die Rechnung von Herr Schmidt für jeden beliebigen Betrag das Ergebnis liefert, dass sich Tauschen lohnt, so braucht er den Umschlag gar nicht zu öffnen, sondern kann gleich den anderen Umschlag nehmen. Es kann aber nicht sein, dass der andere Umschlag immer besser ist, da ja beide Umschläge vor dem Öffnen offensichtlich gleichwertig sind.

Die Denkfalle

Unser Wahrnehmungs- und Denkapparat ist ständig dabei, Strukturen zu suchen und zu erkennen. Das ist ein Erfolgsrezept. Diese Strukturerwartung drückt sich in der uns angeborenen Prägnanztendenz aus. Die Prägnanztendenz bewirkt unter anderem, dass wir kleine Unterschiede einebnen und Symmetrien überbetonen. In diesem Sinne ist das Indifferenzprinzip eine Ausprägung der Prägnanztendenz. Der grundsätzlich nützliche Mechanismus der Prägnanztendenz schießt bisweilen über das Ziel hinaus. Er wird dann zur Denkfalle.

Beim Umschlagparadoxon tut sich eine solche Denkfalle auf. Das Indifferenzprinzip scheint anwendbar zu sein, denn mit 50-prozentiger Wahrscheinlichkeit wird der Umschlag mit dem größeren Betrag und mit ebenfalls 50-prozentiger Wahrscheinlichkeit der mit dem kleineren Betrag gewählt. Wenn wir den größeren Betrag 2Z und den kleineren Betrag Z nennen, gewinnt Herr Schmidt Z Euro oder verliert Z Euro durch den Tausch. Um eine sinnvolle Tauschstrategie zu ermitteln, ist jedoch die bedingte Wahrscheinlichkeit erforderlich. Es geht hier erstens um die Wahrscheinlichkeit des Falles, dass 50 Euro in einem und 100 Euro im anderen Umschlag stecken und zweitens um die Wahrscheinlichkeit des Falles, dass es sich um 100 Euro und 200 Euro handelt. Nur wenn die Wahrscheinlichkeiten dieser beiden Fälle gleich sind, hat Herr Schmidt mit seinen Überlegungen recht. Und über die Wahrscheinlichkeiten dieser Fälle ist tatsächlich nichts bekannt. Da die Anzahl von denkbaren Fällen unendlich groß ist, können diese Wahrscheinlichkeiten gar nicht alle gleich sein. Das Indifferenzprinzip ist also ausgehend von einem aufgedeckten Betrag x auf die Ereignisse „doppelter Betrag“ (2x) und „halber Betrag“ (x/2) aus grundsätzlichen Erwägungen heraus nicht anwendbar. In der Denkfallen-Sammlung ^[1] wird das an ein paar Rechenbeispielen weiter verdeutlicht.^[2]

Der folgende Abschnitt geht der Frage auf den Grund, ob bei einer bekannten oder geschätzten Wahrscheinlichkeitsverteilung ein Tausch für gewisse Beträge sinnvoll sein kann, und ob es überhaupt eine Wahrscheinlichkeitsverteilung geben kann, bei der ein Tausch immer angezeigt ist.

Die Lösung

Die bedingte Wahrscheinlichkeit, den kleineren Umschlag gewählt zu haben, unter der Bedingung, dass im geöffneten Umschlag der Betrag n ist, hängt von n ab. Sie kann für manche Beträge 50% sein (dann lohnt sich das Tauschen tatsächlich); es gibt aber keine Wahrscheinlichkeitsverteilung, die für jeden beliebigen Betrag im Umschlag konstant eine bedingte Wahrscheinlichkeit von 50% liefert. Tauschen abhängig vom Inhalt des Umschlags kann eine höhere Gewinnerwartung liefern. Tauschen unabhängig vom Inhalt liefert hingegen keine höhere Gewinnerwartung.

Eine exakte Berechnung, ob ein Tausch abhängig vom Inhalt des Umschlags sinnvoll ist, sieht folgendermaßen aus: Bezeichnet man mit

• S_n das Ereignis, dass die Sekretärin von Herrn Lemke n Euro in den einen und 2n Euro in den anderen Umschlag steckt, mit
• p_n = P(S_n) die Wahrscheinlichkeit dieses Ereignisses, mit
• B_n das Ereignis, dass Herr Schmidt n Euro im Briefumschlag findet, und mit
• A_n das Ereignis, dass Herr Schmidt n Euro im anderen Briefumschlag findet,

so gilt für die Wahrscheinlichkeit, dass Herr Schmidt n Euro im Briefumschlag findet

$P\left(B_n\right)=P\left(B_n|S_n\right)P\left(S_n\right)+P\left(B_n|S_{n/2}\right)P\left(S_{n/2}\right)=\frac{p_n}{2}+\frac{p_{n/2}}{2}$,

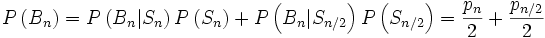für die bedingte Wahrscheinlichkeit, dass Herr Schmidt den doppelten Betrag im anderen Briefumschlag findet

$P\left(A_{2n}|B_n\right)=\frac{P\left(A_{2n}\cap B_n\right)}{P\left(B_n\right)}= \frac{\frac{1}{2}p_n}{\frac{p_n}{2}+\frac{p_{n/2}}{2}}=\frac{p_n}{p_n+p_{n/2}}$,

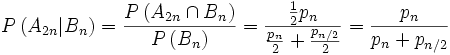und für die bedingte Wahrscheinlichkeit, dass Herr Schmidt den halben Betrag im anderen Briefumschlag findet

$P\left(A_{n/2}|B_n\right)=\frac{P\left(A_{n/2}\cap B_n\right)}{P\left(B_n\right)}= \frac{\frac{1}{2}p_{n/2}}{\frac{p_n}{2}+\frac{p_{n/2}}{2}}=\frac{p_{n/2}}{p_n+p_{n/2}}$.

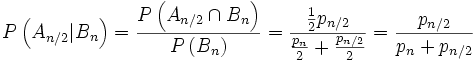Sofern der Erwartungswert der Verteilung mit den korrekten Wahrscheinlichkeiten existiert, erhielte man

$E=2n\frac{p_n}{p_n+p_{n/2}}+\frac{n}{2}\frac{p_{n/2}}{p_n+p_{n/2}}=\frac{4p_n+p_{n/2}}{2\left(p_n+p_{n/2}\right)}n$.

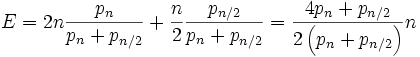Zu tauschen würde sich demnach genau dann auszahlen, wenn E > n gilt; dies ist genau dann der Fall wenn 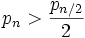$p_n > \frac{p_{n/2}}{2}$. Verteilungen, die diese Bedingung für alle möglichen n erfüllen, lassen sich zwar konstruieren, besitzen dann aber keinen endlichen Erwartungswert, sodass die oben angedeutete Argumentation, die zu einem Widerspruch führt, bereits aus formalen Gründen unzulässig ist.

Zudem widerspricht die Annahme, dass beliebig hohe Beträge im Umschlag sein können, der praktischen Einschränkung, dass niemand, also auch nicht Hr. Lemke, unendlich viel Geld zur Verfügung hat.

Beispiel

Wenn man eine Wahrscheinlichkeitsverteilung annimmt, mit der die Sekretärin von Herrn Lemke das Geld in die Briefumschläge verteilt, lässt sich die Geschichte sehr gut simulieren. Beispielsweise sei angenommen, die Sekretärin bestimmt den Betrag mit einem fairen Würfel. Zeigt der Würfel k Augen, so steckt sie 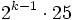$2^{k-1} \cdot 25$ Euro in den einen und 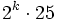$2^k \cdot 25$ Euro in den anderen Umschlag. Herr Schmidt findet dann mit Wahrscheinlichkeit 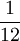$\frac{1}{12}$ den Betrag 25 Euro im Umschlag, mit Wahrscheinlichkeit je 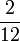$\frac{2}{12}$ einen der Beträge 50, 100, 200, 400 oder 800 Euro, und wieder mit Wahrscheinlichkeit 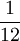$\frac{1}{12}$ den Betrag 1600 Euro. Tauscht er nicht, so beträgt der Erwartungswert des Geldgeschenkes also

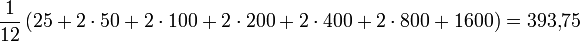$\frac{1}{12}\left(25+2\cdot 50+2\cdot 100+2\cdot 200+2\cdot 400+2\cdot 800+ 1600\right) = 393{,}75$ Euro.

Tauscht Herr Schmidt in jedem Fall, so ändert sich sein Erwartungswert nicht, da er insbesondere auch den Betrag von 1600 Euro tauscht, obwohl er in diesem Fall nichts gewinnen kann. Vermutet Herr Schmidt aber, dass wohl kaum mehr als 1000 Euro im Umschlag sind, und entscheidet sich daher, dann und nur zu tauschen, wenn höchstens 500 Euro im Umschlag sind, so ändern sich die Wahrscheinlichkeiten: Nach dem Tausch hat Herr Schmidt dann weiterhin mit Wahrscheinlichkeit 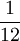$\frac{1}{12}$ den Betrag 25 Euro im Umschlag, ebenso mit Wahrscheinlichkeit je 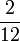$\frac{2}{12}$ einen der Beträge 50, 100, oder 200 Euro, den Betrag von 400 Euro allerdings nur mehr mit Wahrscheinlichkeit 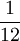$\frac{1}{12}$ (da Herr Schmidt bei 800 Euro nicht mehr tauscht), dafür aber mit Wahrscheinlichkeit 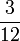$\frac{3}{12}$ den Betrag von 800 Euro, und wieder mit Wahrscheinlichkeit 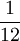$\frac{1}{12}$ den Betrag 1600 Euro. Der Erwartungswert des Geldgeschenkes ist nun also

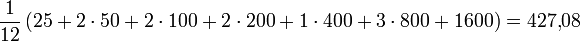$\frac{1}{12}\left(25+2\cdot 50+2\cdot 100+2\cdot 200+1\cdot 400+3\cdot 800+ 1600\right) = 427{,}08$ Euro.

Schätzt Herr Schmidt die Situation besser ein und beschließt, erst ab 1000 Euro aufs Tauschen zu verzichten, kann er den Erwartungswert sogar auf 460,62 Euro erhöhen; wird er aber zu gierig und tauscht beispielsweise bis zu 2000 Euro, so fällt er wieder auf den Ausgangswert 393,75 Euro zurück.

Für Herrn Schmidt ist es natürlich schwierig, die Sekretärin von Herrn Lemke richtig einzuschätzen; wesentlich ist aber, dass das Paradoxon verschwindet, sobald man irgendeine konkrete Wahrscheinlichkeitsverteilung für das Verhalten der Sekretärin von Herrn Lemke annimmt. Je nach Tauschstrategie von Herrn Schmidt ändert sich der Erwartungswert des Geldgeschenks; die Strategie „Tausche immer“ ist aber gleich gut (oder schlecht) wie die Strategie „Tausche nie“.

Anwendung des Zwei-Zettel-Spiels

In obigem Beispiel wurde angenommen, dass bekannt ist, nach welchem Prinzip die Sekretärin die Geldbeträge verteilt. Unter dieser Annahme lassen sich leicht Gewinnstrategien angeben. Die Problemformulierung enthält aber keine Information über die Arbeitsweise der Sekretärin. Es gibt allerdings auch eine allgemeine Gewinnstrategie für Herrn Schmidt, die diese Annahme nicht benötigt. Diese Strategie besteht darin, dass Herr Schmidt, bevor er den Umschlag öffnet, eine Zufallszahl Z wählt, die alle Werte zwischen 0 und unendlich annehmen kann, deren Verteilung aber ansonsten beliebig ist. Dann öffnet er den Umschlag und findet den Betrag n. Ist der gefundene Betrag n kleiner gleich Z, so tauscht er den Umschlag; ist der Betrag n größer als Z, so behält er den Umschlag. Diese Strategie geht auf Thomas M. Cover zurück.^[3] Wie im Artikel Zwei-Zettel-Spiel erklärt, erhöht er so theoretisch seine Chancen, den größeren Betrag zu erhalten.^[4][5]

Angenommen, Hr. Schmidt entschließt sich das Zwei-Zettel-Spiel anzuwenden. Enthalten die Briefumschläge die Beträge A und B, wobei A der kleinere Betrag sein soll, und öffnet Hr. Schmidt zuerst den Umschlag mit Inhalt A, so wechselt er, falls 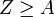$Z\geq A$. Die bedingte Erwartung seines Gewinns beträgt dann

$E_{A;AB}= P(Z\geq A)\cdot B+P(Z<A)\cdot A$.

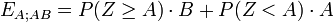Öffnet er zuerst den Umschlag mit Inhalt B, so wechselt er, falls 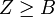$Z\geq B$. Die bedingte Erwartung seines Gewinns beträgt dann

$E_{B;AB}= P(Z\geq B)\cdot A+P(Z<B)\cdot B$.

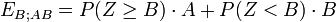Insgesamt beträgt die bedinge Erwartung bei fixen Inhalten, aber vor der Wahl des ersten Umschlags 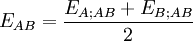$E_{AB}=\frac{E_{A;AB}+E_{B;AB}}{2}$. Tauscht er immer oder tauscht er nie, berägt sein Erwartungswert 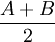$\frac{A+B}{2}$. Für Z wählt Hr. Schmidt beispielsweise eine Zufallsvariable Z, die exponentialverteilt mit Erwartungswert 1000 ist, also 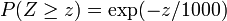$P(Z\geq z)=\exp(-z/1000)$. Falls die Sekretärin wie im oben angegebem Beispiel das Geld in die Briefumschläge verteilt, ergibt sich insgesamt folgender Erwartungswert des Geldgeschenkes:

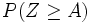
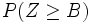
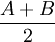
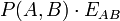
	A	B	P(A,B)	$P(Z\geq A)$	EA;AB	$P(Z\geq B)$	EB;AB	EAB	$\frac{A+B}{2}$	$P(A,B)\cdot E_{AB}$
	25	50	1/6	0,975	49,382	0,951	26,219	37,801	37,5	6,300
	50	100	1/6	0,951	97,561	0,904	54,758	76,160	75,0	12,693
	100	200	1/6	0,904	190,484	0,819	118,127	154,305	150,0	25,718
	200	400	1/6	0,819	363,746	0,670	265,936	314,841	300,0	52,473
	400	800	1/6	0,670	688,128	0,449	620,268	644,198	600,0	107,366
	800	1600	1/6	0,449	1159,463	0,202	1438,483	1298,973	1200,0	216,496
Summe			1							421,046

Der Erwartungswert des Geldgeschenkes beträgt bei dieser Vorgangsweise also 421,046 Euro. Das ist zwar weniger als bei der optimalen Strategie (tausche bei weniger als 1000 EUR), bei der der Erwartungswert 427,08 Euro beträgt; aber jedenfalls mehr als bei der "Tausche-nie" oder "Tausche-immer"-Vorgangsweise, bei der der Erwartungswert 393,75 beträgt. Wie aus der Tabelle ersichltich, ist in jeder Zeile E_AB größer als 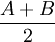$\frac{A+B}{2}$, es gilt nämlich:

$E_{AB}= \frac{A+B}{2} + \frac{B-A}{2}\Big(P(Z\geq A)-P(Z\geq B)\Big)$.

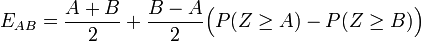Der genaue Erwartungswert hängt natürlich stark von der Wahl der Verteilung von Z ab, ist aber immer höher als bei der "Tausche-nie" oder "Tausche-immer"-Vorgangsweise.

Geschichte des Paradoxons

Das Umtauschparadoxon lässt sich zumindest bis 1953 zurückverfolgen und wurde damals in einem Buch des belgischen Mathematikers Maurice Kraitchik sinngemäß folgendermaßen formuliert:

Zwei gleich wohlhabende Personen treffen einander und wollen die Inhalte ihrer Geldbörsen vergleichen. Keiner weiß, wie viel Geld der andere in der Börse hat. Sie vereinbaren folgendes Spiel: Derjenige, der weniger Geld in der Börse hat, gewinnt den Inhalt der Geldbörse des anderen. Falls beide gleich viel haben sollten, behält jeder sein Geld. Nun könnte einer der beiden folgende Überlegung anstellen: „Angenommen, ich habe den Betrag A in meiner Börse. Dann ist das das Maximum, das ich verlieren kann. Mit Wahrscheinlichkeit 0,5 gewinne ich allerdings und habe danach mehr als 2A. Daher ist das Spiel günstig für mich.“ Der andere könnte allerdings genauso argumentieren. Aus Symmetriegründen muss das Spiel aber fair sein. Worin liegt der Trugschluss dieser Argumentation?^[6]

Martin Gardner verbreitete das Rätsel 1982 in seinem Buch Aha! Gotcha, ebenfalls in der Gestalt eines Geldbörsenspiels.^[7]. Die heutige Form mit den beiden Briefumschlägen wurde 1989 von Barry Nalebuff formuliert.^[8]

Siehe auch

Verwandte Themen, bei denen man aus Teilinformation die optimale Entscheidung des Restproblems treffen kann:

• Gefangenenparadoxon
• Odds-Strategie
• Sekretärinnenproblem
• Ziegenproblem
• Zwei-Zettel-Spiel

Einzelnachweise

1. ↑ Denkfallen und Paradoxa
2. ↑ Denkfallen und Paradoxa: Umtauschparadoxon (Briefumschlag-Paradoxon)
3. ↑ Franz Thomas Bruss,Der Ungewissheit ein Schnippchen schlagen, Spektrum der Wissenschaft, 6/2000. 106-107.
4. ↑ R Christensen and J Utts, Bayesian Resolution of the Exchange Paradox, The American Statistician 1992
5. ↑ Dov Samet, Iddo Samet, and David Schmeidler, One Observation behind Two-Envelope Puzzles (PDF)
6. ↑ Maurice Kraitchik, La mathématique des jeux, 1953
7. ↑ Martin Gardner, Aha! Gotcha, 1982
8. ↑ Barry Nalebuff, Puzzles: the other person's envelope is always greener, Journal of Economic Perspectives 3, 1989