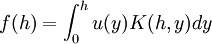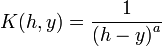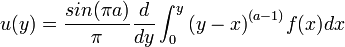- Abel-Transformation
-
Die Abelsche Integralgleichung ist eine spezielle Volterrasche Integralgleichung 1. Art. Sie hat die Form:
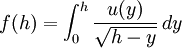 .
.
wobei f (h) vorgegeben ist und u (y) die gesuchte Funktion ist. Die Volterrasche Integralgleichung 1. Art ist allgemeiner als
definiert mit einer Kernfunktion K. Speziell für Kernfunktionen K der Form
mit 0 < a < 1 gibt es eine allgemeine Lösungsmethode durch Rückführung auf die Formel für die Eulersche Betafunktion. Es ergibt sich:
Bei der Abelschen Integralgleichung ist
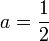 .
.Der durch die Verallgemeinerung der Abelsche Integralgleichung für 0 < a < 1 ausgedrückte Zusammenhang zwischen den Funktionen f(h) und u(y) wird auch als Abel-Transformation bezeichnet, das heißt f (h) ist die Abel-Transformierte von u (y). Die durch die erwähnte Lösungsmethode für 0 < a < 1 gelieferte Formel für u(y) ergibt die Umkehrformel der Abeltransformation.
Anwendung und Geschichte
Niels Henrik Abel untersuchte 1823 als einer der ersten Integralgleichungen, und zwar in Zusammenhang mit einem mechanischen Problem. Bis dahin war die Mechanik vorwiegend von Differentialgleichungen bestimmt. Abel betrachtete einen Körper, der sich unter dem Einfluss der Schwerkraft entlang einer in einer vertikalen Ebene gelegenen Kurve von P1(x0,y0) nach (0,0) bewegt.
Ausgehend von der klassischen Formel für Geschwindigkeit
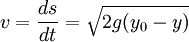 kommt man durch Integration über die Strecke auf die Fallzeit
kommt man durch Integration über die Strecke auf die Fallzeit 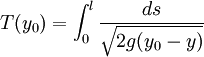 .
.Durch die Substitution
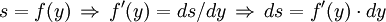 zu der endgültigen Form:
zu der endgültigen Form: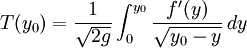 .
.Kennt man die Kurve f(y), erhält man so die Fallzeit. Abel betrachtete auch das umgekehrte Problem: ist die Fallzeit vorgegeben, erhält man eine Abelsche Integralgleichung für die unbekannte Funktion f'(y).
Weitere Anwendungen der Abelschen Integralgleichung bzw. der Abel-Transformation gibt es in der Astrophysik, in der Geophysik (Herglotz-Wiechert-Methode der Bestimmung der Geschwindigkeitsverteilung aus Ankunftszeiten von seismischen Wellen) und beispielsweise in der Bestimmung der Atmosphären-Daten von Planeten durch Radio-Okkultation. Wie in der ursprünglichen Anwendung sind das typische inverse Probleme.
Literatur
- Smirnow Lehrgang der höheren Mathematik, Teil 4, VEB Deutscher Verlag der Wissenschaften, Berlin 1979, S.5
- Flügge Methoden der mathematischen Physik, Bd.1, Springer Verlag, S.130
- Abel Transformation bei Math World
Wikimedia Foundation.