- Abgestumpftes Tetraeder
-
Das Friauf-Polyeder (abgestumpftes Tetraeder, Tetraederstumpf) ist ein Polyeder (Vielflächner), das durch Abstumpfung der Ecken eines Tetraeders entsteht und zu den archimedischen Körpern zählt. Anstatt der vier Ecken des Tetraeders befinden sich nun dort vier gleichseitige Dreiecke, die dreieckigen Flächen des Tetraeders werden zu regelmäßigen Sechsecken. Der Name geht zurück auf den Chemiker James B. Friauf, der dieses Polyeder zum ersten Mal als Grundlage des Aufbaus von MgZn2 beschrieb.[1] [2]
Das Friauf-Polyeder ist ein typisches Koordinationspolyeder mit der Koordinationszahl 12 in intermetallischen Verbindungen wie den Laves-Phasen. In MgNi2 beispielsweise wird das Magnesium von 12 Nickelatomen in Form eines Friauf-Polyeders umgeben. Die nächsten vier benachbarten Magnesiumatome umgeben das zentrale Magnesiumatom des Friauf-Polyeders in Form eines Tetraeders und befinden sich genau über den Sechsecken, sie werden auch als Kappen bezeichnet. Für dieses vierfach überkappte Friauf-Polyeder ergibt sich somit eine Koordinationszahl von 12 + 4 = 16.
Inhaltsverzeichnis
Formeln
Größen eines Tetraederstumpfs mit Kantenlänge a Volumen 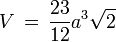
Oberflächeninhalt 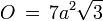
Umkugelradius 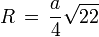
Kantenkugelradius 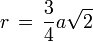
Flächen-Flächen-Winkel
≈ 70,53° (Hexagon–Hexagon)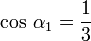
Flächen-Flächen-Winkel
≈ 109,47° (Hexagon–Trigon)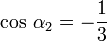
Kartesische Koordinaten
Die kartesischen Koordinaten der Eckpunkte können lauten, bei Mittelpunkt im Ursprung:
- (±3, ±1, ±1),
- (±1, ±3, ±1),
- (±1, ±1, ±3),
wobei von diesen 24 Koordinaten jene 12 auszuwählen sind, die eine ungerade Zahl an Pluszeichen (1 oder 3) und damit eine gerade an Minuszeichen (2 oder 0) haben, oder umgekehrt.
Einzelnachweise
- ↑ http://laves.mpie.de/laves_phases.html
- ↑ http://etd.caltech.edu/etd/available/etd-11112004-102634/
Weblinks
- Eric W. Weisstein: Truncated Tetrahedron auf MathWorld (engl.)
Tetraederstumpf · Kuboktaeder · Hexaederstumpf · Oktaederstumpf · Rhombenkuboktaeder · Großes Rhombenkuboktaeder · Dodekaederstumpf · Ikosaederstumpf · Ikosidodekaeder · Abgeschrägtes Hexaeder · Rhombenikosidodekaeder · Großes Rhombenikosidodekaeder · Abgeschrägtes Dodekaeder
Rhombendodekaeder · Triakistetraeder · Triakisoktaeder · Tetrakishexaeder · Deltoidalikositetraeder · Pentagonikositetraeder · Rhombentriakontaeder · Hexakisoktaeder · Triakisikosaeder · Pentakisdodekaeder · Deltoidalhexakontaeder · Pentagonhexakontaeder · Disdyakistriakontaeder
Wikimedia Foundation.


