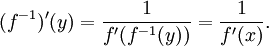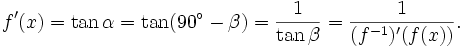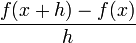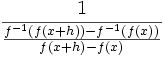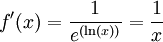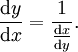Ableitung der Umkehrfunktion
- Ableitung der Umkehrfunktion
-
Die Umkehrregel ist eine Regel der Differentialrechnung. Sie besagt, dass für eine umkehrbare (d. h. bijektive) Funktion f,
- die an der Stelle x differenzierbar ist und
- dort keine waagerechte Tangente besitzt, d.h. für die
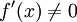 gilt,
gilt,
auch ihre Umkehrfunktion f − 1 an der Stelle y = f(x) differenzierbar ist mit Ableitung
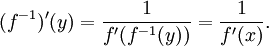
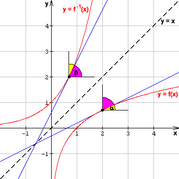
Veranschaulichung der Umkehrregel
Die Gültigkeit dieser Gleichung kann man sich gut an einer Skizze verdeutlichen: Die Bildung der Umkehrfunktion entspricht einer Vertauschung der Koordinaten x und y. Die Graphen der Funktion f und ihrer Umkehrfunktion f − 1 sind also zueinander symmetrisch bezüglich der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung y = x. Die Ableitung einer Funktion an einer bestimmten Stelle entspricht der Steigung der zugehörigen Tangente, also gleich dem Tangens des Neigungswinkels gegenüber der Waagrechten. Damit erhält man:
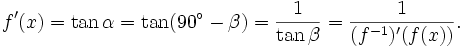
Beweisskizze
Die Umkehrregel kann direkt gezeigt werden, indem man den Differenzenquotient
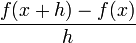
dahingehend umformt, dass er zu
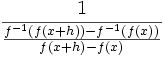
wird, um anschließend mit t = f(x + h) − f(x) zu substituieren. Beim Grenzübergang für 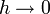 und damit auch
und damit auch 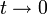 folgt die Behauptung.
folgt die Behauptung.
Beispiel
Für den natürlichen Logarithmus f(x) = ln(x) lautet die Umkehrfunktion:
- f − 1(x) = ex.
Die Ableitung der Umkehrfunktion ist:
- (f − 1)'(x) = ex
Dann lautet die Ableitung der Funktion:
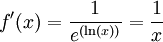
Alternative Formulierungen und Verallgemeinerungen
Alternative Voraussetzungen
Fordert man die Stetigkeit der ersten Ableitung von f, so genügt bereits die Voraussetzung 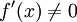 , da daraus direkt
, da daraus direkt 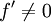 auf einem kleinen Bereich um x und daraus wiederum die Existenz der Umkehrfunktion von f auf diesem kleinen Bereich folgt (man betrachte dazu die Monotonie von f!). Von dieser Grundidee geht man bei der mehrdimensionalen Verallgemeinerung der Umkehrregel, dem Satz von der inversen Abbildung, aus.
auf einem kleinen Bereich um x und daraus wiederum die Existenz der Umkehrfunktion von f auf diesem kleinen Bereich folgt (man betrachte dazu die Monotonie von f!). Von dieser Grundidee geht man bei der mehrdimensionalen Verallgemeinerung der Umkehrregel, dem Satz von der inversen Abbildung, aus.
Abweichende Schreibweisen in der Physik und anderen Naturwissenschaften
In der Physik und anderen Naturwissenschaften wird manchmal die leibnizsche Schreibweise mit Differentialen benutzt. Die Umkehrregel nimmt dann die folgende Gestalt an:
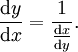
Verallgemeinerungen
Die Umkehrregel lässt sich auf die Ableitungen von Funktionen in mehreren Dimensionen verallgemeinern. Die mehrdimensionale Entsprechung der Umkehrregel ist der Satz von der Umkehrabbildung.
Literatur
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Ableitung (Mathematik) — Die Differential bzw. Differenzialrechnung ist ein Gebiet der Mathematik und ein wesentlicher Bestandteil der Analysis. Sie ist eng verwandt mit der Integralrechnung, mit der sie unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird.… … Deutsch Wikipedia
Satz über die Umkehrfunktion — Der Satz von der impliziten Funktion ist einer der wichtigsten Sätze in der Analysis. Er beinhaltet ein relativ einfaches Kriterium, wann man eine implizite Gleichung oder ein Gleichungssystem (lokal) eindeutig auflösen kann. Inhaltsverzeichnis 1 … Deutsch Wikipedia
Satz von der inversen Funktion — Der Satz von der impliziten Funktion ist einer der wichtigsten Sätze in der Analysis. Er beinhaltet ein relativ einfaches Kriterium, wann man eine implizite Gleichung oder ein Gleichungssystem (lokal) eindeutig auflösen kann. Inhaltsverzeichnis 1 … Deutsch Wikipedia
Satz von der impliziten Funktion — Der Satz von der impliziten Funktion ist einer der wichtigsten Sätze in der Analysis. Er beinhaltet ein relativ einfaches Kriterium, wann eine implizite Gleichung oder ein Gleichungssystem (lokal) eindeutig aufgelöst werden kann.… … Deutsch Wikipedia
Trennung der Veränderlichen — Die Methode der Trennung der Veränderlichen, Trennung der Variablen, Separationsmethode oder Separation der Variablen ist ein Verfahren aus der Theorie der gewöhnlichen Differentialgleichungen. Mit ihr lassen sich separierbare… … Deutsch Wikipedia
Separation der Variablen — Die Methode der Trennung der Veränderlichen (auch Trennung der Variablen, Separationsmethode oder Separation der Variablen) ist ein Verfahren aus der Theorie der gewöhnlichen Differentialgleichungen um Differentialgleichungen erster Ordnung der… … Deutsch Wikipedia
Trennung der Variablen — Die Methode der Trennung der Veränderlichen (auch Trennung der Variablen, Separationsmethode oder Separation der Variablen) ist ein Verfahren aus der Theorie der gewöhnlichen Differentialgleichungen um Differentialgleichungen erster Ordnung der… … Deutsch Wikipedia
Lambert-W-Funktion — Der Graph von W(x) für In der Mathematik ist die lambertsche W Funktion (oder Lambert W Funktion), benannt nach Johann Heinrich Lambert, die Umkehrfunktion von f(x): = xex, wobei ex di … Deutsch Wikipedia
Omega-Konstante — Der Graph von W(x) für In der Mathematik ist die lambertsche W Funktion (oder Lambert W Funktion), benannt nach Johann Heinrich Lambert, die Umkehrfunktion von f(x): = xex, wobei ex di … Deutsch Wikipedia
Lambertsche W-Funktion — Der Graph von W(x) für W > −4 und x < 6. Der obere Zweig W ≥ −1 ist die Funktion W0 (principal branch), der untere Zweig mit W ≤ −1 ist die Funktion W−1. In der Mathematik ist die lambertsche W Funktion (oder Lambert W Funktion), auch… … Deutsch Wikipedia
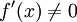 gilt,
gilt,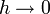 und damit auch
und damit auch 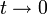 folgt die Behauptung.
folgt die Behauptung.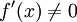 , da daraus direkt
, da daraus direkt 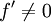 auf einem kleinen Bereich um x und daraus wiederum die Existenz der Umkehrfunktion von f auf diesem kleinen Bereich folgt (man betrachte dazu die Monotonie von f!). Von dieser Grundidee geht man bei der mehrdimensionalen Verallgemeinerung der Umkehrregel, dem Satz von der inversen Abbildung, aus.
auf einem kleinen Bereich um x und daraus wiederum die Existenz der Umkehrfunktion von f auf diesem kleinen Bereich folgt (man betrachte dazu die Monotonie von f!). Von dieser Grundidee geht man bei der mehrdimensionalen Verallgemeinerung der Umkehrregel, dem Satz von der inversen Abbildung, aus.