Absolutkonvexe Menge — Absolutkonvexe Mengen spielen eine wichtige Rolle in der Theorie der lokalkonvexen Räume, da sie in natürlicher Weise zu Halbnormen führen. Inhaltsverzeichnis 1 Definition 2 Beziehung zu Halbnormen 3 Absolutkonvexe Hülle … Deutsch Wikipedia
Satz von Komura — Unter einem nuklearen Raum versteht man in der Mathematik eine spezielle Klasse lokalkonvexer Vektorräume. Viele in den Anwendungen wichtige Räume, z. B. Räume differenzierbarer Funktionen, sind nuklear. Während normierte Räume, insbesondere… … Deutsch Wikipedia
Satz von Komura-Komura — Unter einem nuklearen Raum versteht man in der Mathematik eine spezielle Klasse lokalkonvexer Vektorräume. Viele in den Anwendungen wichtige Räume, z. B. Räume differenzierbarer Funktionen, sind nuklear. Während normierte Räume, insbesondere… … Deutsch Wikipedia
Satz von Kōmura-Kōmura — Unter einem nuklearen Raum versteht man in der Mathematik eine spezielle Klasse lokalkonvexer Vektorräume. Viele in den Anwendungen wichtige Räume, z. B. Räume differenzierbarer Funktionen, sind nuklear. Während normierte Räume, insbesondere… … Deutsch Wikipedia
Beschränkt — Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge… … Deutsch Wikipedia
Beschränkte Menge — Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge… … Deutsch Wikipedia
Gleichmäßig beschränkt — Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge… … Deutsch Wikipedia
Gleichmäßige Beschränktheit — Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge… … Deutsch Wikipedia
Punktweise Beschränktheit — Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge… … Deutsch Wikipedia
Schranke (Mathematik) — Die Eigenschaft der Beschränktheit wird in verschiedenen Bereichen der Mathematik einer Menge zugeordnet. Die Menge wird dann als (nach unten oder oben) beschränkte Menge bezeichnet. Damit ist zunächst gemeint, dass alle Elemente der Menge… … Deutsch Wikipedia
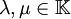 mit
mit 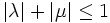 und alle
und alle 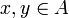 stets
stets 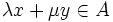 gilt. Damit ist A genau dann absolutkonvex, wenn A ausgewogen und konvex ist. (Dabei steht
gilt. Damit ist A genau dann absolutkonvex, wenn A ausgewogen und konvex ist. (Dabei steht 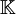 für den Körper der reellen oder komplexen Zahlen.)
für den Körper der reellen oder komplexen Zahlen.)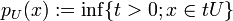 eine Halbnorm auf E. Es gilt
eine Halbnorm auf E. Es gilt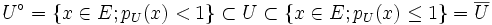 .
.