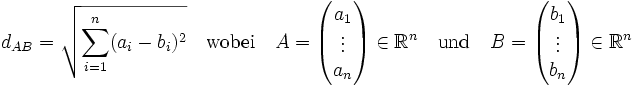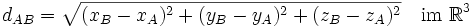- Abstand (Mathematik)
-
Physikalische Größe Name Abstand Größenart Länge Formelzeichen der Größe r Formelzeichen der Dimension L Größen- und
Einheiten-
systemEinheit Dimension SI Meter (m) L Im mathematisch und physikalischen Sinn ist der Abstand, die Entfernung, die Distanz zwischen zwei Punkten, die Länge der Strecke, die durch die beiden Punkte begrenzt wird, also die Länge der gradlinigen Verbindungslinie der beiden Punkte. Der Abstand zwischen zwei Gegenständen ist die Länge der kürzesten Verbindungslinie der beiden Gegenstände, also die Länge der Strecke die durch die beiden einander nächstliegenden Punkte der beiden Gegenstände begrenzt wird. Werden nicht die einander nächstliegenden Punkte zweier Gegenstände betrachtet, so wird dies explizit angegeben oder ergibt sich aus dem Zusammenhang, wie beispielsweise der Abstand der geometrischen Mittelpunkte oder der Schwerpunkte.
Der Bereich der Mathematik, der sich mit der Abstandsmessung beschäftigt ist die Metrik.
Der Abstand, die Entfernung, die Distanz zwischen zwei Werten oder Zeitpunkten wird bestimmt, indem man den Absolutwert ihrer Differenz bildet, das heißt, indem sie voneinander abgezogen werden und vom Ergebnis der Absolutbetrag gebildet wird. Der gemessene Abstand (Entfernung, Distanz) ist unabhängig vom gewählten Referenzpunkt des Koordinatensystems nicht aber von dessen Skalierung (vergleiche Maßstab).
In der beobachtenden Astronomie wird der scheinbare Abstand am Himmel zwischen zwei Himmelsobjekten als Winkelabstand − der Differenz der Winkel, unter denen sie erscheinen − angegeben.
Der Abstand zweier Mengen kann über die Hausdorff-Metrik definiert werden.
Inhaltsverzeichnis
Euklidischer Abstand
Im kartesischen Koordinatensystem ist der Abstand (euklidischer Abstand) zwischen zwei Punkten gleich der Wurzel der Summe der Quadrate der Abstands-Koordinaten:
Der Abstand eines Punkts zu einer Geraden oder einer ebenen Fläche ist der Abstand zum Fußpunkt des darauf gefällten Lots, der zu einer gekrümmten Linie ist stets ein Abstand zu einer ihrer Tangenten.
Abstandsmessung auf gekrümmten Flächen
Auf der Kugeloberfläche wird der Abstand entlang von Großkreisen bestimmt und im Gradmaß oder Bogenmaß angegeben. Zur Berechnung des Abstandes siehe Orthodrome.
Auf dem Erdellipsoid oder anderen konvexen Flächen benutzt man die geodätische Linie oder den Normalschnitt.
In der Geodäsie und den Geowissenschaften spricht man eher von Distanz oder Entfernung, die metrisch angegeben wird.
Siehe auch
Weblinks
Wikimedia Foundation.