- Abzählbare Menge
-
In der Mengenlehre wird eine Menge A als abzählbar unendlich bezeichnet, wenn sie die gleiche Mächtigkeit hat wie die Menge der natürlichen Zahlen
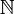 . Dies bedeutet, dass es eine Bijektion zwischen A und der Menge der natürlichen Zahlen gibt, die Menge A also „durchnummeriert“ werden kann.
. Dies bedeutet, dass es eine Bijektion zwischen A und der Menge der natürlichen Zahlen gibt, die Menge A also „durchnummeriert“ werden kann.Zu den höchstens abzählbaren Mengen zählen neben den abzählbar unendlichen auch kleinere, also endliche Mengen. Die Verwendung des Begriffes abzählbar ist nicht einheitlich. Er kann je nach Definition sowohl abzählbar unendlich als auch höchstens abzählbar bedeuten.
Eine Menge, die weder endlich noch abzählbar unendlich ist, wird als überabzählbar bezeichnet.
Inhaltsverzeichnis
Beispiele abzählbar unendlicher Mengen
Natürliche Zahlen
Die Menge der natürlichen Zahlen
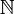 ist per Definition abzählbar unendlich, da sie dieselbe Mächtigkeit wie sie selbst besitzt.
ist per Definition abzählbar unendlich, da sie dieselbe Mächtigkeit wie sie selbst besitzt.Primzahlen
Die Menge der Primzahlen
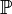 ist ebenfalls abzählbar unendlich, da sie eine Teilmenge der natürlichen Zahlen und nach dem Satz von Euklid auch unendlich ist.
ist ebenfalls abzählbar unendlich, da sie eine Teilmenge der natürlichen Zahlen und nach dem Satz von Euklid auch unendlich ist.n 1 2 3 4 5 6 7 8 … f(n) 2 3 5 7 11 13 17 19 … Ganze Zahlen
Die Menge der ganzen Zahlen
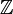 ist abzählbar unendlich, eine Abzählung ist beispielsweise gegeben durch
ist abzählbar unendlich, eine Abzählung ist beispielsweise gegeben durchn 1 2 3 4 5 6 7 8 … f(n) 0 1 −1 2 −2 3 −3 4 … Die Beispiele Primzahlen und ganze Zahlen zeigen, dass sowohl echte Teilmengen als auch Obermengen dieselbe Mächtigkeit besitzen können, im Gegensatz zu endlichen Mengen.
Paare natürlicher Zahlen
Auch die Menge aller Paare
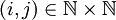 von zwei natürlichen Zahlen ist abzählbar unendlich.
von zwei natürlichen Zahlen ist abzählbar unendlich.Die Unendlichkeit ist wiederum offensichtlich. Schwieriger ist die Frage der Abzählbarkeit. Dafür nutzt man die Cantorsche Paarungsfunktion, die jedem Zahlenpaar (i,j) bijektiv eine natürliche Zahl k zuordnet. Damit kann man alle Zahlenpaare eindeutig nummerieren und somit abzählen.
n 1 2 3 4 5 6 7 8 9 10 … f(n) 1,1 1,2 2,1 1,3 2,2 3,1 1,4 2,3 3,2 4,1 … n-Tupel natürlicher Zahlen
Die Menge aller n-Tupel
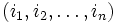 natürlicher Zahlen
natürlicher Zahlen 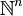 ist ebenfalls abzählbar unendlich. Das zeigt man wiederum durch (n − 1)-malige Anwendung der Cantorschen Paarungsfunktion.
ist ebenfalls abzählbar unendlich. Das zeigt man wiederum durch (n − 1)-malige Anwendung der Cantorschen Paarungsfunktion.Rationale Zahlen
Georg Cantor zeigte mit der so genannten Cantor-Diagonalisierung, dass die Menge der rationalen Zahlen abzählbar ist, ebenso jede Menge der Gestalt
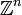 (Tupel ganzer Zahlen). Darüber hinaus existiert noch die Quantoralsymmetrie.
(Tupel ganzer Zahlen). Darüber hinaus existiert noch die Quantoralsymmetrie.Die Abbildung
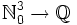 ,
, 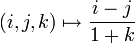 ist surjektiv, also ist die Mächtigkeit von
ist surjektiv, also ist die Mächtigkeit von 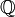 höchstens so groß wie die von
höchstens so groß wie die von 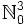 . Da es einerseits unendlich viele Brüche gibt und andererseits die Menge
. Da es einerseits unendlich viele Brüche gibt und andererseits die Menge 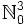 abzählbar unendlich ist, ist auch
abzählbar unendlich ist, ist auch  abzählbar unendlich.
abzählbar unendlich.Algebraische Zahlen
Es sei P ein Polynom mit ganzzahligen Koeffizienten, P(x) = a0 + ... + anxn. Die Höhe von P sei definiert als h(P) = | a0 | + ... + | an | + n. Zu jeder vorgegebenen Höhe > 0 gibt es nur endlich viele Polynome, welche wiederum nur endlich viele Nullstellen besitzen. Die Vereinigung
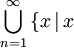 ist Nullstelle eines ganzzahligen Polynoms P mit
ist Nullstelle eines ganzzahligen Polynoms P mit 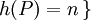 ist gerade die Menge der algebraischen Zahlen
ist gerade die Menge der algebraischen Zahlen 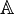 . Als abzählbare Vereinigung endlicher Mengen ist
. Als abzählbare Vereinigung endlicher Mengen ist 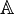 daher abzählbar.
daher abzählbar.Wörter über einem Alphabet
Durch die Anwendung der sogenannten Standardnummerierung über das Alphabet Σ kann man auch die Wörter einer Sprache im Sinne der Mathematik abzählen.
Berechenbare Zahlenfunktionen
Die Menge aller berechenbaren Zahlenfunktionen ist abzählbar unendlich. Man kann eine Standardnummerierung aller denkbaren Bandprogramme angeben. Da die Menge der Bandprogramme größer als die Menge der berechenbaren Funktionen ist (es könnte ja zwei unterschiedliche Programme geben, die dieselbe Funktion berechnen), sind damit die Zahlenfunktionen abzählbar unendlich.
Beispiel einer überabzählbaren unendlichen Menge
Die Menge der reellen Zahlen ist dagegen überabzählbar. Das bedeutet, dass es keine bijektive Abbildung gibt, die jede reelle Zahl auf je eine natürliche Zahl abbildet, siehe Cantors zweites Diagonalargument.
Eigenschaften
- Jede Teilmenge einer (höchstens) abzählbaren Menge ist (höchstens) abzählbar.
- Die Vereinigung zweier (höchstens) abzählbarer Mengen ist (höchstens) abzählbar.
- Allgemeiner ist jede Vereinigung einer abzählbaren Anzahl von (höchstens) abzählbaren Mengen wieder (höchstens) abzählbar.
- Das kartesische Produkt zweier (höchstens) abzählbaren Mengen ist (höchstens) abzählbar.
- Gibt es eine Surjektion von der Menge
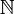 der natürlichen Zahlen auf die Menge A, so ist A höchstens abzählbar.
der natürlichen Zahlen auf die Menge A, so ist A höchstens abzählbar. - Jede aufzählbare Menge ist auch abzählbar.
Siehe auch
- In der Topologie erfüllen „kleine“ topologische Räume ein Abzählbarkeitsaxiom.
- Kardinalzahl (Mathematik)
- Diskretheit
- Hilberts Hotel
Wikimedia Foundation.
