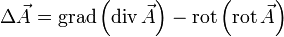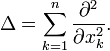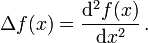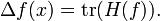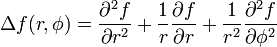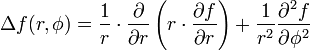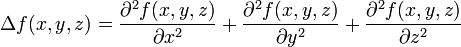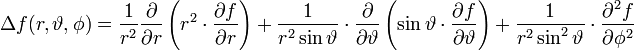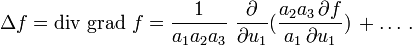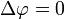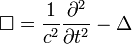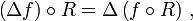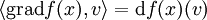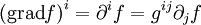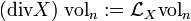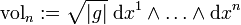Delta-Operator

Der Laplace-Operator Δ ist ein mathematischer Operator (also eine Rechenvorschrift), der zuerst von Pierre-Simon Laplace eingeführt wurde. Er spielt in vielen physikalischen Theorien, insbesondere bei der Beschreibung elektrischer und gravitativer Felder, eine zentrale Rolle und bildet z. B. das Kernstück der Laplace- und Poisson-Gleichung. Im Vakuum beschreibt die Laplace-Gleichung das elektrostatische Potential außerhalb leitender, geladener Körper. Soll dagegen das elektrostatische Potential innerhalb beliebig verteilter, zeitunabhängiger Ladungsdichten berechnet werden, wird die Poisson-Gleichung verwendet. Zusammen mit anderen Ableitungen tritt der Laplace-Operator auch in der Wellengleichung und der Diffusionsgleichung auf. Wie bereits erwähnt, wird der Laplace-Operator oftmals auch bei der Berechnung der Verteilung von Schwerefeldern verwendet.

Mathematisch gesehen ist der Laplace-Operator ein Differentialoperator innerhalb der mehrdimensionalen Analysis. Zudem ist er der einzige partielle Differentialoperator zweiter Ordnung, der mit Rotationen, Translationen und Reflexionen vertauscht.

Definition

Der Laplace-Operator ist für Skalarfelder definiert als:

$\Delta f = \operatorname{div}\left(\operatorname{grad}\,f\right) = \nabla^2 f = \nabla \cdot \nabla f$

Im englischsprachigen Raum wird der Laplace-Operator auch mit der Schreibweise 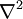$\nabla^2$, mit Bezug zu dem Nabla-Operator $\nabla$, bezeichnet.

Für Vektorfelder gilt:

$\Delta\vec A = \operatorname{grad}\left(\operatorname{div}\,\vec A \right) - \operatorname{rot}\left( \operatorname{rot}\,\vec A \right)$

Durch die Invarianz der Begriffe div, rot und grad, siehe Divergenz, Rotation und Gradient, ist diese Definition vom gewählten Koordinatensystem unabhängig. Wird der Laplace-Operator auf ein Skalarfeld angewendet, liefert er als Ergebnis ein Skalarfeld. Bei der Anwendung auf ein Vektorfeld ist das Ergebnis ein Vektorfeld. Im n -dimensionalen, Euklidischen Raum ergibt sich in kartesischen Koordinaten

$\Delta= \sum_{k=1}^n {\partial^2\over \partial x_k^2}.$

Die Darstellung des Laplace-Operators in anderen Koordinatensystemen ergibt sich mit der Kettenregel aus der Koordinatentransformation.

In einer Dimension reduziert sich der Laplace-Operator auf die zweite Ableitung,

$\Delta f(x) = \frac{\mathrm d^2 f(x)}{\mathrm dx^2}\,.$

Der Laplace-Operator einer Funktion kann auch als Spur ihrer Hessematrix dargestellt werden.

$\Delta f(x) = \mathrm{tr}(H(f)).\,\!$

Darstellung in zwei Dimensionen

Für eine Funktion f(x,y) mit zwei Variablen ergibt die Anwendung des Laplace-Operators in kartesischen Koordinaten

$\Delta f(x,y) = \frac{\partial^2 f(x,y)}{\partial x^2} + \frac{\partial^2 f(x,y)}{\partial y^2}$

In Polarkoordinaten ergibt sich mit f(r,φ)

$\Delta f(r, \phi ) = \frac{\partial^2 f}{\partial r^2} + \frac{1}{r}\frac{\partial f}{\partial r} + \frac{1}{r^2}\frac{\partial^2 f}{\partial \phi^2}$

oder

$\Delta f(r, \phi ) = \frac{1}{r}\cdot\frac{\partial}{\partial r} \left( r\cdot\frac{\partial f}{\partial r} \right) + \frac{1}{r^2}\frac{\partial^2 f}{\partial \phi^2}$

Darstellung in drei Dimensionen

Für eine Funktion f(x,y,z) mit drei Variablen ergibt sich in kartesischen Koordinaten

$\Delta f(x,y,z) = \frac{\partial^2 f(x,y,z)}{\partial x^2} + \frac{\partial^2 f(x,y,z)}{\partial y^2} + \frac{\partial^2 f(x,y,z)}{\partial z^2}$

Die Laplace-Operatoren in Zylinder- und Kugelkoordinaten gelten nur bei Anwendung auf einen Skalar, bei der Anwendung auf einen Vektor müssen noch weitere Terme berücksichtigt werden.^[1] in Zylinderkoordinaten mit f(ρ,φ,z)

$\Delta f ( \rho , \phi , z ) = \frac{1}{\rho} \cdot\frac{\partial}{\partial \rho} \left( \rho\cdot\frac{\partial f}{\partial \rho} \right) + \frac{1}{\rho^2}\cdot\frac{\partial^2 f}{\partial \phi^2} + \frac{\partial^2 f}{\partial z^2}$

in Kugelkoordinaten mit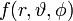 $f ( r , \vartheta , \phi )$

$\Delta f ( r , \vartheta , \phi ) = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \cdot \frac{\partial f}{\partial r} \right) + \frac{1}{r^2 \sin \vartheta} \cdot \frac{\partial}{\partial \vartheta} \left(\sin\vartheta \cdot \frac{\partial f}{\partial \vartheta} \right) + \frac{1}{r^2 \sin^2\vartheta} \cdot \frac{\partial^2 f}{\partial \phi^2}$

In dieser Gleichung kann man hinter dem Gleichheitszeichen anstelle des ersten Terms auch

$\frac{1}{r}\cdot \frac{\partial^2}{\partial r^2}(r\cdot f) \quad \mbox{oder} \quad \left(\frac{\partial^2}{\partial r^2}+\frac{2}{r}\cdot\frac{\partial}{\partial r}\right)f$

schreiben.

Die Greensche Funktion des Laplace-Operators hat die Form: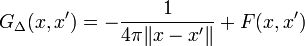

$G_{\Delta}(x, x') = -\frac{1}{4\pi\|x-x'\|} + F(x,x')$ mit ΔF(x,x') = 0.

Es gilt dann: ΔG_Δ(x,x') = δ(x − x') mit der Delta-Distribution δ. Diese Greensche Funktion wird in der Elektrodynamik als Hilfsmittel zur Lösung von Randwertproblemen benötigt.

Darstellung in krummlinigen Orthogonalkoordinaten

In beliebigen krummlinigen Orthogonalkoordinaten, z. B. in sphärischen Polarkoordinaten, Zylinderkoordinaten, elliptischen Koordinaten, u.s.w., gilt dagegen mit 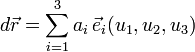$d\vec r=\sum\limits_{i=1}^3 a_i\,\vec e_i(u_1, u_2,u_3)\,$, wobei 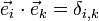$\vec e_i\cdot \vec e_k = \delta_{i,k}\,$ ist (=1 für i=k, =0 sonst), wegen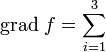 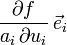${\rm{grad\,\,}} f = \sum_{i=1}^3\,$$\frac{\partial f}{a_i\,\partial u_i} \,\vec e_i$ , wobei also nicht die du_i, sondern die Größen 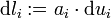$\mathrm dl_i:= a_i\cdot\mathrm{d}u_i$ die physikalische Dimension einer „Länge“ haben, eine allgemeinere Beziehung für den Laplace-Operator, wobei zu beachten ist, dass die a_i nicht konstant sind, sondern von u₁, u₂ und u₃ abhängen können:

$\Delta f ={\rm{div\,\,grad\,\,}}f = \frac{1}{a_1a_2a_3}\,\,\frac{\partial}{{\partial u_1}}(\frac{a_2a_3\,\partial f}{a_1\,\partial u_1})\,+\dots\, .$

Dabei sind durch die Punkte, ..., zwei Terme angedeutet, die aus dem ausgeschriebenen Term durch zyklische Permutation nach dem Schema 1 -> 2, 2 -> 3, 3 -> 1 hervorgehen. Für noch allgemeinere Koordinaten gilt die Laplace-Beltrami-Beziehung (siehe unten).

Bemerkungen

Der Laplace-Operator tritt beispielsweise in der Laplace-Gleichung

$\Delta\varphi = 0$

auf. Zweimal stetig differenzierbare Lösungen dieser Gleichung heißen harmonische Funktionen.

Da die Hesse-Matrix die Matrix aller zweiten, partiellen Ableitungen ist, ist der Laplace-Operator gerade die Spur der Hesse-Matrix.

Der Laplace-Operator ergibt zusammen mit der zweiten Zeitableitung den d'Alembert-Operator:

$\square = \frac{1}{c^2} \frac{\partial ^2}{\partial t^2}- \Delta$

Dieser Operator kann als eine Verallgemeinerung des Laplace-Operators Δ auf den Minkowski-Raum betrachtet werden.

Eigenschaften

Der Laplace-Operator ist drehsymmetrisch, das heißt, ist f eine zweimal differenzierbare Funktion und R eine Drehung, so gilt

$\left( \Delta f \right)\circ R=\Delta\left(f\circ R\right)\,,$

wobei „$\circ$“ für die Verkettung von Abbildungen steht.

Diskreter Laplace-Operator und Bildverarbeitung

Hauptartikel: Laplace-Filter

In der Bildverarbeitung wird der Laplace-Operator zur Kantendetektion eingesetzt. Eine Kante taucht als Nulldurchgang der zweiten Ableitung des Signals auf. Auf ein diskretes Signal g_n bzw. g_nm wird der Laplace-Operator über eine Faltung angewendet. Dabei kann man folgende einfache Faltungsmasken verwenden:

1D-Filter: $\vec{D}^2_x=\begin{bmatrix}1 & -2 & 1\end{bmatrix}$

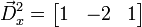
2D-Filter: $\mathbf{D}^2_{xy}=\begin{bmatrix}0 & 1 & 0\\1 & -4 & 1\\0 & 1 & 0\end{bmatrix}$

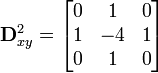
Für das 2D-Filter gibt es noch eine zweite Variante:

2D-Filter: $\mathbf{D}^2_{xy}=\begin{bmatrix}1 & 1 & 1\\1 & -8 & 1\\1 & 1 & 1\end{bmatrix}$

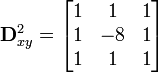
Diese Faltungsmasken erhält man durch die Diskretisierung der Differenzenquotienten.

Laplace-Beltrami-Operator

Für den Laplace-Operator, der ursprünglich stets als Operator des euklidischen Raumes verstanden wurde, gab es mit der Formulierung der riemannschen Geometrie die Möglichkeit der Verallgemeinerung auf gekrümmte Flächen und Riemannsche bzw. pseudo-riemannsche Mannigfaltigkeiten. Dieser allgemeinere Operator wird als Laplace-Beltrami-Operator bezeichnet. Er wird, wie der Laplace-Operator, als Divergenz des Gradientenfeldes definiert. Um den Laplace-Beltrami-Operator herzuleiten werden also verallgemeinerte Ausdrücke für die Divergenz und den Gradienten auf einer riemannschen Mannigfaltigkeit benötigt.

Der Gradient einer skalaren Funktion auf einer Mannigfaltigkeit 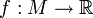$f:M\rightarrow \mathbb{R}$ ist ein Vektorfeld auf M, das mit Hilfe des Skalarprodukts 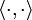$\,\langle\cdot,\cdot\rangle$ dadurch definiert ist, dass an jedem Punkt x der Mannigfaltigkeit M für alle Tangentialvektoren 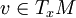$\,v \in T_x M$ die Gleichung

$\langle \mbox{grad} f(x) , v \rangle = \mathrm d f(x)(v)$

gilt. Hierbei bezeichnet df(x) die äußere Ableitung der Funktion f an der Stelle x, aufgefasst als Linearform auf dem Tangentialraum. Die kontravarianten Komponenten des Gradienten können mit

$\left(\mbox{grad} f\right)^i = \partial^i f = g^{ij} \partial_j f$

berechnet werden. In dieser Formel wird die einsteinsche Summenkonvention benutzt. Das bedeutet, dass über j von 1 bis n summiert wird. Die g^ij sind dabei die Komponenten der Inversen des metrischen Tensors g_ij. Es gilt also 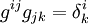$g^{ij}g_{jk}=\delta^i_k$. Dabei ist 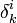$\delta^i_k$ das Kronecker-Delta.

Die Divergenz eines Vektorfeldes X in einer Mannigfaltigkeit kann über die Lie-Ableitung L_X des Volumenelements entlang des Vektorfeldes X

$(\mbox{div} X) \; \mathrm{vol}_n := \mathcal{L}_X \mathrm{vol}_n$

definiert werden. Wenn g für den metrischen Tensors der Mannigfaltigkeit steht, ist das Volumenelement in lokalen Koordinaten durch:

$\mathrm{vol}_n := \sqrt{|g|} \;\mathrm dx^1\wedge \ldots \wedge \mathrm dx^n$

gegeben. Dabei ist | g | : = | detg_ij | der Betrag der Determinante des metrischen Tensors. Die dxⁱ sind die Kovektoren zu den Basisvektoren

$\partial_i := \frac {\partial}{\partial x^i}$

und bilden eine Basis des Dualraums des lokalen Koordinatensystems. 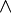$\, \wedge$ ist das Keilprodukt. In lokalen Koordinaten gilt also:

$\mbox{div} X = \frac{1}{\sqrt{|g|}} \partial_i \left(\sqrt {|g|} X^i\right).$

Der Laplace-Beltrami-Operator schreibt sich damit in der Anwendung auf eine skalare Funktion f insgesamt als

$\Delta f = \mbox{div grad} \; f = \frac{1}{\sqrt {|g|}} \partial_i \left(\sqrt{|g|} \partial^i f\right)$.

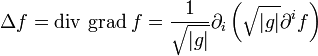Unter Benutzung der Produkt- und Kettenregel lässt sich das auch in die folgende Formel umformen:

$\Delta f = \partial_i \partial^i f + (\partial^i f) \partial_i \ln \sqrt{|g|}$.

Da im dreidimensionalen, euklidischen Raum mit kartesischen Koordinaten | g | = 1 gilt, ergibt sich 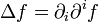$\Delta f = \partial_i \partial^i f$ was genau dem gewöhnlichen Laplace-Operator entspricht. Wird die Minkowski-Metrik mit Signatur (+,-,-,-) oder (-,+,+,+) benutzt, ergibt sich dagegen der D'Alembert-Operator.

Setzt man in der Formel für den Laplace-Beltrami-Operator die Darstellung des (euklidischen) metrischen Tensors in Polar-, Zylinder- oder Kugelkoordinaten ein, so erhält man die Darstellung des üblichen Laplace-Operators in diesen Koordinatensystemen, denn in Polar- und Zylinderkoordinaten gilt | g | = r bzw. | g | = ρ und in Kugelkoordinaten | g | = rsinθ.

Neben der Darstellung mit Hilfe des Volumenelements gibt es auch eine Darstellung, die die Christoffel-Symbole verwendet:

$\Delta f = g^{ij}\left(\frac{\partial^2 f}{\partial x^i \partial x^j} - \Gamma_{ij}^k \frac{\partial f}{\partial x^k} \right)$.

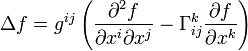Mit der äußeren Ableitung d und der verallgemeinerten Divergenz lässt sich noch die folgende Identität auf Mannigfaltigkeiten formulieren und beweisen:

$\int_M \mathrm df(X) \;\mathrm{vol}_n = - \int_M f \mbox{div} X \;\mathrm{vol}_n$.

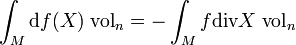Für geeignete Funktionen f und h gelten die Formeln:

$\int_M f\Delta h \;\mathrm{vol}_n = - \int_M \langle \mbox{grad} f, \mbox{grad} h \rangle \;\mathrm{vol}_n = \int_M h\Delta f \;\mathrm{vol}_n$.

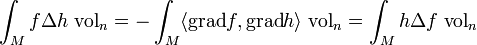Der Laplace-deRham-Operator ist eine Verallgemeinerung des Laplace-Beltrami-Operators.

Einzelnachweise

1. ↑ http://mathworld.wolfram.com/VectorLaplacian.html

Literatur

• Otto Forster: Analysis 3. 3. Auflage, vieweg studium, 1984
• Martin Schottenloher: Geometrie und Symmetrie in der Physik, vieweg Lehrbuch, 1995

Weblinks

• Wie „krümme“ ich Nabla und Delta? – Herleitung des Nablaoperators für orthonormal krummlinige Koordinaten auf www.matheplanet.com