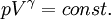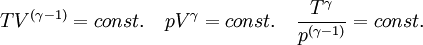- Adiabatengleichung
-
Siméon-Denis Poisson (* 21. Juni 1781 in Pithiviers (Département Loiret); † 25. April 1840 in Paris) war ein französischer Physiker und Mathematiker.
Poisson begann 1798 Mathematik an der École polytechnique zu studieren, wo er die Bekanntschaft von Laplace und Lagrange machte. Bereits 1802 wurde er dort Professor und übernahm 1806 den Lehrstuhl von Jean Baptiste Joseph Fourier, nachdem dieser von Napoleon nach Grenoble geschickt worden war. Poisson war ein Schüler von Pierre Simon Laplace und beschäftigte sich mit den Grundlagen der Wellentheorie, arbeitete über Akustik, Elastizität und Wärme sowie über die elektrischen Eigenschaften von festen Körpern. 1812 publiziert er seine Erweiterung der Laplace-Gleichung um die Oberflächenladung. 1838 veröffentlichte er seine Wahrscheinlichkeitstheorie (darin auch Poisson-Verteilung, die Abraham de Moivre bereits bekannt war).
Die Beziehung zwischen Druck p und Volumen V bei adiabatischer Zustandsänderung ging als Poissonsches Gesetz in die Physik ein:
In der Thermodynamik, auch Kalorik oder Wärmelehre genannt, spricht man eher von den Poissonschen Gleichungen:
Dabei ist γ der so genannte Adiabatenexponent (oft auch κ genannt). Nach ihm ist auch die Poissonzahl μ benannt. Sie gibt an, in welchem Verhältnis die Längsdehnung ε und die gleichzeitig eintretende Querkontraktion εq zueinander stehen, wenn ein Stab auf Zug beansprucht wird. Die Poissonzahl, auch Querkontraktionszahl genannt, liegt stets zwischen 0 und 0,5.
Als Mathematiker arbeitete Poisson auf vielen Gebieten, unter anderem der Differentialgeometrie, Infinitesimalrechnung und Wahrscheinlichkeitsrechnung. Mehrere mathematische Begriffe sind mit seinem Namen verbunden, z.B. Poissonsche Differentialgleichung, Poissonsche Integralformel, Poisson-Kern, Poisson-Verteilung, Poisson-Gleichung, Poissonzahl und Poisson-Klammer. Insgesamt veröffentlichte er über 300 Arbeiten.
Nachdem die Gesetze der Deviation von Matthew Flinders gefunden worden waren, stellte Poisson sie in mathematischer Form dar.
Er ist namentlich auf dem Eiffelturm verewigt, siehe: Die 72 Namen auf dem Eiffelturm.
Weblinks
- S.-D. Poisson: Lehrbuch der Mechanik. Zweiter Teil, Berlin 1836 (Digitalisat Łódź)
- Eintrag im Mathematikerstammbaum
- Siméon Denis Poisson im MacTutor History of Mathematics archive (englisch)
Personendaten NAME Poisson, Siméon Denis KURZBESCHREIBUNG französischer Physiker und Mathematiker GEBURTSDATUM 21. Juni 1781 GEBURTSORT Pithiviers (Dep. Loiret) STERBEDATUM 25. April 1840 STERBEORT Paris
Wikimedia Foundation.