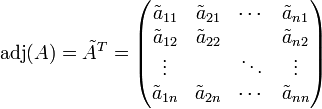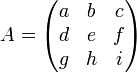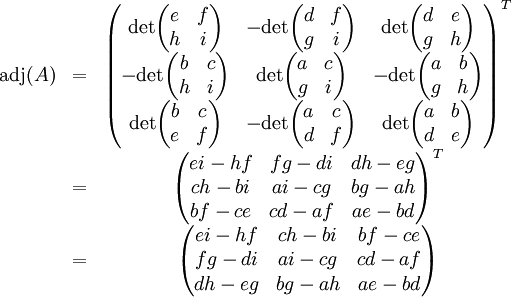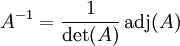- Adjunkte Matrix
-
Die Adjunkte, klassische Adjungierte oder komplementäre Matrix einer Matrix ist ein Begriff aus dem mathematischen Teilgebiet Lineare Algebra. Man bezeichnet damit die transponierte Matrix der Cofaktoren, also der vorzeichenbehafteten Minoren.
Es ist hierbei zu beachten, dass dem Indexpaar (i,j) der Cofaktor
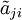 zugeordnet wird. Die Cofaktoren
zugeordnet wird. Die Cofaktoren 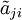 berechnen sich zu
berechnen sich zu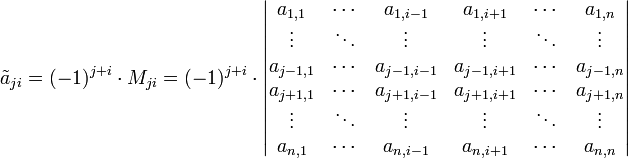 .
.
Die Minoren Mji sind die Werte der Unterdeterminanten der Matrix A, die durch Streichen der j-ten Zeile und der i-ten Spalte entstehen.
Da die Adjunkte in heutigen Lehrbüchern selten auftaucht und in älteren Werken die Notation alles andere als eindeutig war, ist Vorsicht geboten. Oft wird dieselbe Notation für die Adjunkte und die Adjungierte (also bei reellen Matrizen deren Transponierte, bei komplexen Matrizen deren konjugiert-transponierte, bei allgemeineren Räumen mit Hilfe des zu Grunde liegenden Skalarproduktes oder Sesquilinearproduktes) verwendet.
Beispiel
Eine beliebige
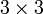 -Matrix hat die Form
-Matrix hat die FormDie Adjunkte zu dieser Matrix ist
Eigenschaften
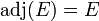 , wobei E eine Einheitsmatrix ist.
, wobei E eine Einheitsmatrix ist.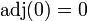 , wobei 0 eine Nullmatrix ist.
, wobei 0 eine Nullmatrix ist.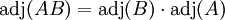
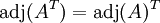
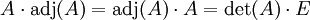
Berechnung der Inversen einer Matrix
Hauptartikel: Reguläre Matrix
Die einzelnen Spalten der Inversen einer Matrix A werden jeweils von der Lösung des Gleichungssystems Ax = ej mit dem j-ten Einheitsvektor auf der rechten Seite gebildet. Berechnet man diese mit der Cramer’schen Regel, so erhält man die Formel
Wikimedia Foundation.